For our examples we are going to identify handwritten numbers between 0 and 9. Humans (past a certain age) find this task quite easy, even with everyone writing their numbers slightly different. Creating a program for a computer to do this is more difficult since there isn't an exact pixel map that it can simply match. It has to be able to deal with determining what varying darkness of pencil marks and find what inexact shapes (in this case numbers) the image represents.

Remember that images on your TV or computer screens are really made up of thousands or millions of tiny little dots called pixels. By itself, a pixel would just look like dot of color whether that be black, white, red, green, blue or something in between. For our examples we are only going to use gray-scale (black, white and ranges of gray.) 8-bit graphics (similar to games on the original Nintendo) mean that there are (2^8 = )256 levels of a color between 0 and 255, which in our case 0 gives us white, 64 a light gray, 191 a dark gray and 255 gives us black. Rather than having to deal with all these numbers, we can just use a range from 0 (white) to 1 (black) with all the grays in between.

The above image has the number 1 written on a 14x14 grid and you can see where the darkest marks in the middle are given a value of 1 (on the right hand side,) grays given varying decimal levels (.1 to .9) and the area with no writing having zeroes (white areas.) This grid gives us 196 pixels each with a value, which is what we are going to use to feed into the number recognition program (i.e. inputs.) A little later in this series, we are going to use this data set to train our program to recognize 28x28 pixel handwritten digits. This means that our neural net will end up needing 784 input nodes, one for each pixel, and 10 output nodes, one for the each digit 0-9.

In the end we are going to setup a neural network that we are going to give a large number of numbers to identify, tell it what the correct answer is, and allow it to refine itself so it can perform the way we want it to. This process is called a form of supervised learning called backpropagation where it can compare it's determined answer we say it should be, then feeding this new information back into it's own input to run through the system again. We'll get more into that later on, I just wanted you to have an idea of where this is going.

Design Basics: Perceptions

The perception is an early, basic design for learning programs and though it has limitations, it's a great place to give you the general idea of how neural nets work. If we were to use only perceptions to solve our problem of identifying a written number, the best answer we could get would be that an image would either be a specific number or not (such as 5 or not 5.) But we want it to be able to give an answer of 0-9, which we we eventually built up to being able to handle. For now, just get a bit more comfortable on how inputs are fed in, weights are applied and the outputs given.

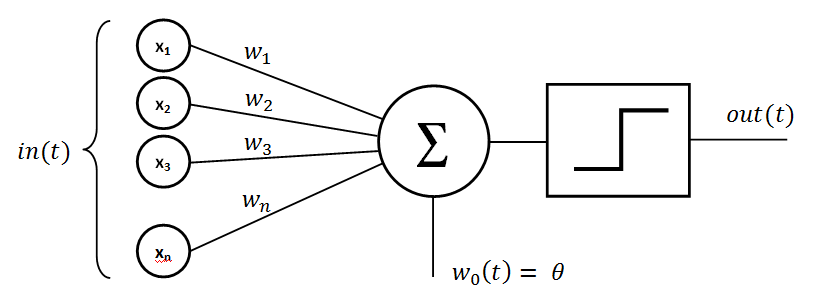
Now don't let this picture scare you as it may not make sense at first sight, it's really not that bad. Just follow along and we will step through this piece by piece.

On the far left we see x(1), x(2), x(3) ... x(n) which are simply our inputs. n is just the total number of inputs we have. Say we have 5 pixels (making n = 5) that are either white (with a value of 0) or black (with a value of 1,) we would then have inputs x(1), x(2), x(3), x(4) and x(5).

As you can see each input has a line with a w that connects it to the Σ (which simply adds things together.) The w's are weights (ours will be between 0 and 1) applied to each input. For example say you are looking to buy a car and your 3 main factors are that:

x1. The car costs less that $20,000
x2. The car is red.
x3. The car is a Ford.

You absolutely can not spend more than the $20,000 so it's weight is will be 1. You would rather like the car to be red but would be open to other colors, so we set that weight at 0.75. Finally, you are not terribly concerned if the car is a Ford versus another brand, so we set that weight to 0.25.

Our perceptron will give an answer on whether to buy the car (an output of 1) or not to buy the car (an output of 0) based on it fitting your preferences. To determine if you buy the car, we are going to say the total of the three weighted inputs (value of each input multiplied by its weight/importance) needs to be above 1.24.

As a concrete example, you are looking at a Red Ford that costs $25,000.
x1 = 0 (because it costs more than $20,000)
x2 = 1 (because it is red)
x3 = 1 (because it is a Ford)

Just to rewrite our weights from above:
w1 = 1 (absolutely must have a car less than $20,000)
w2 = .75 (somewhat important to have a red car)
w3 = .25 (a little important the car is a Ford)

The weighted inputs equal:
x1 * w1 = (0) * (1) = 0
x2 * w2 = (1) * (.75) = 0.75
x3 * w3 = (1) * (.25) = 0.25

The Σ just means to add up all of the pieces and give the sum. So running through this we would get:
Σ = x1w1 + x2w2 + x3*w3 = 0 + 0.75 + 0.25 = 1.0

Now remember how I said above our perceptron would only say to buy the car if it's value was above 1.24? This value is called our threshold and is seen in the image as w0(t) = θ. So in our case θ = 1.24.

That funny looking figure in the square is what is called a step (or activation) function. When Σ > 1.24 it will give a 1 (or an answer of yes) and if Σ <= 1.24 it will give a 0 (or an answer of no.)

**[NOTE: We will be replacing this step/activation function with what is called a sigmoid in the near future. This is due to the step function not being continuous (i.e. it had an abrupt jump vs a smooth curve) which prevents calculus from being applied effectively. But the general idea will be the same and a more in depth explanation will be provided.]

Let's look at how we've set this up and the values we've chosen for weights and the threshold (θ.) For our system to output a 1, saying to buy the car, it has to have the car be under $20,000 AND either be red OR a Ford. Choosing the weights and the threshold allows us to have a slightly more complex system to incorporate your preferences. If we simply said 2 out of 3 factors had to be satisfied, it would say to buy a red Ford that you couldn't afford (which in this case we don't want.) While this is a rather cheesy example, you can see how we could extend this systems to incorporate more buying factors (as an input and weight/importance) but we would have to adapt the threshold to make sure it gave the answers you wanted.

As we add more inputs it quickly becomes difficult to find good values for weights and thresholds to make the system act the way we want. In the sense of the 28x28 pixel grid of a handwritten number it would be unwieldy to do this. So this is where we start applying various training (supervised vs unsupervised) and learning methods (such as back-propagation) to let the system refine itself while running.

Fully getting into how image recognition works takes some building up and it's important to have a grasp of the basics. This series will continue to build upon itself leading to identifying digits from this data set with python and various libraries.

Are you new to Steemit and Looking for Answers? - Try https://www.steemithelp.net.

Image Sources:
Digitized Numbers Gif
Number Pixel Map
Perceptron