On Monday, August 8, 2016, a set of accounts that all started with the name supercomputing dominated the mining queue. People were speculating how this was done. Some thought @supercomputing built a GPU miner for STEEM, others thought they just had access to a lot of cheap CPU resources. But everyone agreed it was certainly unusual behavior.

The behavior was even more unusual than most people might expect. People looked at the blockchain history for @supercomputing's various accounts and found that the accounts' active keys were being changed very frequently. In fact, the active key for an account was changed and then later in the same block a valid PoW was submitted that used that new active key as part of its mining process. This was the smoking gun strongly indicating this was a hack and not just someone throwing a ridiculous amount of computation power at mining Steem. It became quickly clear to me, after a short review of the mining algorithm, that @supercomputing was likely solving some part of the mining algorithm backwards to find an active key that satisfied the mining algorithm for a given precomputed PoW, thereby bypassing the heavy computational work normally needed to solve a PoW.

I informed @dan how I thought this hack was done and gave my recommended fix to the mining algorithm. With the latest v0.13 hardfork, the mining algorithm has been changed to patch this vulnerability.

This post goes into the heavy technical details of what exactly the vulnerability in the original mining algorithm was and how @supercomputing likely exploited it to dominate the mining queue.

Review of old mining algorithm

The intention behind the design of Steem's unique mining algorithm

First, we need to review the old vulnerable mining algorithm in detail. A new mining algorithm was necessary for Steem because it needed to integrate well with DPoS (delegated proof of stake) and its deterministic and precise block production. The intention behind the Steem mining algorithm design was to: tie the PoW computation to a particular private key that controlled access to the user's funds; and, require the PoW computation to depend on the latest block ID.

The second condition is something every other cryptocurrency's mining algorithm (that I know of) also has because their PoW can only be included in the header of the generated block, and generated blocks need to build off the previous block to form the blockchain. But Steem does mining differently. Finding the PoW is decoupled from generating the blocks, which is what allows for deterministic and precise block intervals. However, it is still beneficial to make the PoW depend on the latest block ID for a few different reasons. Most importantly it does the best job in utilizing the computational work done as an additional security metric for identifying the correct chain. But it also reduces the memory and computational requirements of nodes in the network if they only need to validate the submitted PoW against the latest block ID (particularly in making sure that the identical PoW was not already submitted in the past). Instead of storing all valid PoW submitted to the blockchain for all time (to check for duplicates), the system could only need to store all valid PoW submitted to the blockchain that depended on the last N block IDs (where N is a constant number that determines how many consecutive block IDs in the past, counting backwards from the head block, can be used as the dependency for a valid PoW accepted into a block building off the current head block). By choosing the smallest value of N = 1, the memory requirements for the duplicate check are minimized and implementation becomes even simpler (the database simply stores the last valid PoW submitted by each witness in their corresponding witness object). Using N = 1 also has an advantage when it comes to latency requirements on witness/miner block production nodes. With N = 1 and with Steem's 3 second block intervals, it means that a node has less than 3 seconds to solve a PoW and broadcast that transaction containing the PoW to the rest of the network. This means latency of the node's internet connection becomes really important in mining. A server with a high-latency internet connection will not be very successful (if at all) in finding a valid PoW that is accepted into the blockchain. So Steem's mining algorithm also acts sort of like a proof of network latency in addition to proof of computation power used.

The first condition is a novel (to my knowledge) innovation in Steem's mining algorithm, which requires the miner doing computational work to find a PoW to possess the active key of the account that will eventually be rewarded for finding that PoW. This feature makes mining pools more inconvenient in Steem than other cryptocurrencies. The mining pool operator would either have to trust all the miners to not use their active private key (which they must give to them for them to be able to mine) to do any damage to their account, or more likely use an account that has no liquid funds, is not used for anything other than mining, and run an online bot with owner key permissions (which is not great practice from a security perspective) to monitor the account for malicious activity and regularly update the active keys. Mining pools are further disadvantaged by the fact that mining rewards come in the form of vested Steem Power which take 2 years to fully withdraw. Now I may be wrong about this but I believe the mining pool resistant nature of Steem's mining algorithm was just a nice side effect and the main purpose of the algorithm's dependence on an ECDSA (Elliptic Curve Digital Signature Algorithm) signature using the miner's private key was to: prevent attackers from stealing other people's found PoW and claiming it as their own; and making GPU miners much more difficult to implement (to build a GPU miner, one needs to create a shader implementation of ECDSA, which would be useful for improving the performance of all applications using ECDSA, such as Steem). Because the account that eventually claims the reward is tied into the PoW via the account's active key due to the mining algorithm, an attacker cannot change the miner account in the PoW to their own without invalidating the PoW (unless their account has the same active key as the miner they steal from; see note at end of this paragraph) or having to do a lot of computational work to fix the PoW which is identical to them just solving the PoW themselves in the first place. (Note that the attacker can in theory still claim another user's PoW as their own if they, for example, create and broadcast a transaction that first changes their active key to that of the miner they are stealing from, then submits a PoW with the work field copied from the PoW submitted to the network by the miner they are stealing from, and then changes the active key back. But this would only work if this transaction is accepted into the new block before the PoW transaction of the miner that they are stealing from. So pulling this off in practice is not easy unless the attacker is colluding with the witnesses. Nevertheless, the changes to mining algorithm in v0.13 have also closed this potential attack vector which as far as I know had never been exploited prior to the hardfork.)

Pseudocode of Steem's old mining algorithm

The old mining algorithm (which has now, as of hardfork v0.13, been changed) for Steem could be summarized with the following pseudocode:

1) hash1     = SHA256(latest_block_id)

2) hash2     = hash1 except for the first 64-bits replaced by some nonce (basically some random number selected to try to make the final work value have a sufficient number of leading 0 bits)

3) input     = SHA256(hash2)

4) sig       = ECDSA signature (in 65-byte format) of input using d (the active private key) and k (which is just another nonce used for signing)

5) sig_hash  = SHA256(sig)

6) pubkey    = Recover public key (33-byte format) corresponding to the private key that would have signed sig_hash with signature sig

7) work      = SHA256(pubkey)

work must have sufficient number of leading 0 bits matching the current mining difficulty target

Better understanding steps 4 and 6 requires the reader to first understand how the Elliptic Curve Digitial Signature Algorithm (ECDSA) works.

Some quick background on Elliptic Curve Cryptography and ECDSA

I'm going to assume you know at least a little bit about how Elliptic Curve Cryptography (ECC) works (particularly the one used in Bitcoin and Steem), although I will try to summarize the most relevant parts (for this post) in this section.

There is a scalar type which is simply an integer within the range 0 to 2^256 - 1, inclusive. I will use lower case English letters to represent scalar variables. Since the scalar is just a number, it can be represented in memory using 32 bytes. Those 32 bytes are then simply used as the byte string when serializing the scalar for use in, for example, a cryptographic hash.

There is the point type which is a mathematical group that can be thought of as a point on a special 2D curve (the elliptic curve) defined by two coordinates which are finite fields (similar to the scalar you can just think of them as a finite set of integers except between 0 and p-1, inclusive, where p is called the field order and is an integer that is a little smaller than 2^256). I will use upper case English letters to represent point variables, such as Q. I can refer to one of the two field coordinates of the point using the dot notation: Q.x (for the x-coordinate of the point) or Q.y (for the y-coordinate of the point). Due to symmetry of the elliptic curve about the x-axis, the Q.y coordinate is nearly redundant with the exception of one bit of information describing whether the point is above the y = 0 line or below it. The point type can be represented in a compact form using 33 bytes (the last 32 bytes to represent the x-coordinate field, in a way similar to a serialized scalar, and the first byte to just represent which side of the y = 0 line the point is on), which is how it is typically serialized in Steem code).

There are a finite number of distinct valid points on the elliptic curve and all of them can be reached using the expression q G (which is a scalar q multiplying the special elliptic curve base point G to generate a new point on the elliptic curve) for some scalar q. A quick note on multiplying a scalar to a point: 3 G = G + G + G and adding two points of an elliptic curve together to get another point on the curve is some well-defined operation for which you don't need to be concerned about the details for this post. By the way, if I wanted to refer to the x-coordinate field of the point 3 G, I would use the expression (3 G).x.

The scalars can also be added, subtracted and multiplied (and you can even take a modular multiplicative inverse ), just like regular integers, but if we want the scalars to remain closed under these arithmetic operations, they need to be done using modular arithmetic. Furthermore, once we start mixing the scalars with the points (like with the scalar multiplying the point), all of this scalar modular arithmetic needs to happen with a modulus of n, where n is the order of the elliptic curve (it is yet another integer that is a little smaller than 2^256). For example, if we let q_1 q_2 = 2 mod n (which says scalar q_1 multiplied by scalar q_2 is congruent with the scalar 2 modulo n), we can then define the point Q = q_2 G and say that the point q_1 Q is equivalent to the point 2 G, which is true even when q_1 q_2 > n. And then using the regular properties of scalar arithmetic you are likely familiar with, we can also say that the point 2 q_3 G (where q_3 = {q_1}^{-1} mod n) is equivalent to the point Q.

Now with that quick background on ECC, I can describe ECDSA. An ECDSA signature is the pair (r, s) where both r and s are non-zero scalars (it can also have one extra bit of information included in the signature which will be described shortly). For the signature (r, s) on the cryptographic hash e of the byte string representing some arbitrary-length message being signed (all cryptographic hashes used here will use SHA256 and therefore they are simply just another scalar) to be a valid signature signed by the private key d (the corresponding public key is simply the point d G), r and s must of course be non-zero but also the following must be true:

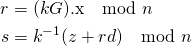
$\begin{align*} r &= (k G)\text{.x} \mod n \ s &= k^{-1} (z + r d) \mod n \end{align*}$

where z is a scalar equal to the $L_n$

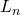leftmost bits of e where $L_n$

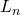is the bit length of n, and the signing nonce k is an arbitrarily chosen scalar satisfying $k \in [1, n-1]$ and satisfying the constraint that r and s must be non-zero. (Note: although k is arbitrary, the same value must never be used for a given private key d to sign two different messages, i.e. different values of z, otherwise the two signatures will leak the private key d. Therefore k is usually either chosen randomly or deterministically generated from a cryptographic hash depending on both z and d.)

Assuming the signature on the message hash is valid, the public key Q corresponding to the private key that was used to sign the message can be recovered using the signature and the message hash (or really z which can be derived from the message hash) as follows:
Let K be one of the two possible points (which of those two is usually determined by the bit included in the serialization of the signature) with K.x equivalent to r. Then,

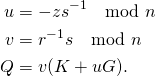
$\begin{align*} u &= -z s^{-1} \mod n \ v &= r^{-1} s \mod n \ Q &= v (K + u G). \end{align*}$

There are two potentially valid choices for the point K selected above (one above the y = 0 line and one below it). When doing a signature verification, one could simply compare the Q resulting from either choice of K to the given public key, and if any of them are equivalent, then the signature could be considered valid. But to recover the public key corresponding to the private used to generate the sigature, one extra bit of information is needed (which side of the y = 0 line that the point K = k G fell on). In Steem code, when the signature (r, s) is serialized, it is actually stored as a 65 byte string (rather than a 2*32 = 64 byte string) because the first byte stores that 1 bit of information needed for recovering the public key (usually called rec_id).

The recovery process described above can of course still be followed to generate a recovery public key Q even if the signature on the message hash was not generated using ECDSA and a private key corresponding to that public key Q. This is what step 6 in the original Steem mining algorithm does where the signature used is sig and the hash of the message used is sig_hash. The "recovered" public key from that process is then denoted pubkey in the above pseudocode.

The vulnerability in the original mining algorithm

The original Steem mining algorithm has a serious vulnerability that allows one to bypass the computational work normally required to find a valid PoW. One only needs to find a valid PoW the normal way once (for any block ID), and then they can use the intermediate values generated via the algorithm and a little bit of mathematics to easily (as in little computational work required) modify the PoW such that it satisfies the algorithm for any given block ID but still computes the exact same work output scalar. Now one might think that this isn't actually a problem because they reasonably assume that the blockchain would not accept an otherwise valid PoWs with a work field that is identical to that of another valid PoW previously submitted to the blockchain, but the duplicate check doesn't exactly work that way (as described in the previous section). Only the work value of the last PoW submitted by an account is stored in the database in order to save memory, which was a perfectly fine and sensible optimization under the assumption that it was not computationally easy to modify the PoW in such a way to make it valid for any given block ID while keeping the same work output. But as I will show shortly within this section, that assumption is not valid.

Without that assumption holding, an attacker could bypass the heavy computational work needed to mine in Steem by doing the following. They would first spend some time to generate enough PoWs (while storing some important intermediate values used in the computation) with unique work outputs for all the accounts they expect to have in the mining queue at any given time (e.g. roughly 120 or so) that satisfy a difficulty target that is higher than what they expect the system to reach (e.g. a target of roughly 35 which corresponds to a mining queue length of 125 seemed reasonable). That computational work only needs to be done once. Then at each block, one of the attacker's accounts not already in the mining queue can grab the latest_block_id and one of the precomputed PoW intermediate values (which have a work output not already stored as the last work of any of the attacker's accounts), then quickly (within a millisecond) calculate the corresponding private key necessary to make the new PoW valid according to the mining algorithm, and then submit a transaction that first changes that account's active public key to the one corresponding to the computed private key and then submits that new PoW to the blockchain.

I believe that is exactly what @supercomputing did that allowed him to dominate the mining queue. Actually, for some reason @supercomputing didn't batch the operation to change the active key and the operation to submit the PoW together into one transaction. That would have been the smarter way to execute the hack, but I guess @supercomputing didn't realize that operations could be batched together into a single atomic transaction in Steem. So looking at the blockchain history of their various accounts, one can deduce several cases in which, due to network latency issues, the transaction to submit the PoW either arrived to a node prior to the transaction to change the active key or the transaction to submit the PoW arrived to a node so late that it was considered for inclusion into a block that came after the block including the corresponding active key change transaction, which in either case would mean that PoW would not be valid at the time it arrived to a node and thus not officially accepted into the blockchain. This is likely why you see far more account change operation than PoW submission operations in the account history of @supercomputing's various accounts.

So how is it possible to create a PoW that satisfies the mining algorithm for any given block ID without needing to do the computationally heavy steps? First a valid PoW that satisfies the desired difficult target needs to be precomputed in the normal way (except the values k and sig from the intermediate steps used to calculate the valid PoW are saved). Using sig one can simply follow steps 5 to 7 of the mining algorithm to deterministically generate the same work that was originally generated (the one that meets the desired difficulty target). If one wants to use the old work value for the "new PoW" valid for a new latest_block_id they must somehow satisfy the constraint imposed by step 4 given a value of input generated by following steps 1 to 3. In order to avoid doing heavy computational work, the attacker should not have to iterate through various nonces. So let's say a fixed nonce (of any arbitrary value) is always used, which then determines the value of input (which then deterministically determines the z scalar used in ECDSA) for a given latest_block_id with no degrees of freedom available the attacker. The attacker must also use the exact same sig (which means the same scalars r and s as well as the same rec_id) as before otherwise steps 5 to 7 would not generate the same work as before. Because r is deterministically determined from k with no degrees of freedom available, the attacker is also forced to use the same signing nonce k as before. The problem is thus reduced to simply finding the active private key d which satisfies the equation 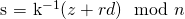$s = k^{-1} (z + r d) \mod n$ given fixed n, z, k, r, s, which turns out to be a problem which is computationally easy to solve. The attacker simply computes d using the formula: 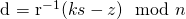$d = r^{-1} (k s - z) \mod n$ .

With the appropriate active private key d computed, the attacker can then change their account's active public key to the one corresponding to the private key d (i.e. d G), which then makes the PoW using the old value of work a valid PoW for that account and for the given lastest_block_id. This process can be done (again very quickly) for any given latest_block_id using the same precomputed k and sig.

The fix

After reading the previous section, it should hopefully be clear what the problem was. The work field could be computationally decoupled from the latest_block_id by exploiting a degree of freedom, the active private key d, in the mining algorithm that could be solved for quickly in such a way to still satisfy the mining algorithm's constraints even without needing to change the value of work. The simplest solution is to recouple work to latest_block_id in a more direct way, i.e. the cryptographically secure dependence on latest_block_id should be introduced to work after that critical ECDSA signature step. This can simply be done by changing step 7 of the above pseudocode to read work = SHA256(input || pubkey) which says that work is the SHA256 cryptographic hash of the message consisting of the pubkey concatenated to the end of input. With this change, it is virtually impossible to reuse an old work value (as in a work value valid for an old block ID) for a new PoW that should be valid for a new latest_block_id. So, the miner is forced to find a valid PoW with a new work value through actually computationally heavy work, by iterating through nonces until they get a work value that meets the current difficulty target.

However, that fix alone is not enough to force users to follow the intended algorithm. While that modified algorithm does force users to actually do heavy computational work to find the PoW, it is still possible to bypass all the ECC steps and essentially reduce the algorithm to a SHA256 hashing algorithm similar to that of Bitcoin. Then it becomes so much easier to build GPU miners and even ASICs since the ECC steps can be completed bypassed during the computationally heavy iteration to find a valid PoW. An attacker would simply iterate the nonce, compute new_input by step 3, and then skip to step 7 (of the modified algorithm) to calculate new_work = SHA256(new_input || pubkey) except where the pubkey is just the old pubkey instead of the one that would be derived from new_input, and then repeat as many times as needed until new_work meets the target difficulty. At this point, the attacker can solve for the private key needed to make new_input match with the old sig in the constraint imposed by step 4 (which is an easy computation). Credit should be given to the Steemit team for discovering this additional vulnerability in even the modified mining algorithm that was described in the previous paragraph.

One way to attempt to fix that vulnerability is to not accept a PoW if the submitting account changed their active key in that block, thereby forcing existing accounts to use the active key they had prior to gaining the information of the latest_block_id that they would need to execute the hack that reduces the mining algorithm to just SHA256 hashing. The problem with this approach is that mining in Steem also allows for the creation of brand new accounts, and brand new accounts must specify their keys at the same time their PoW is submitted.

So the real solution is to simply get rid of the degree of freedom provided when the system allows the user to arbitrarily choose the private key d (or at least the system should allow no more of a degree of freedom than that allowed by iterating a nonce or account name which changes the pseudorandom cryptographic hash output that is used as the private key). So the private key d should instead be deterministically determined by a cryptographic hash dependent on the latest_block_id, miner_account_name (this is to necessary to prevent the PoW from being stolen by another account within the same block), and the nonce. input should also depend on those three values, so it can simply be defined as the SHA256 cryptographic hash of the private key d. The rest of the algorithm is more or less kept the same.

Notice that by getting rid of the user-choice of the private key, the mining account's active private key is no longer necessary to find a PoW. So the first condition of Steem's mining algorithm described in the section describing the old mining algorithm no longer holds true and so its implications may not necessarily hold true either. However, as was discussed earlier, mining pool operators could still operate even with the old algorithm with just a little inconvenience. The main deterrence to mining pools is not the requirement of possessing the active private key to mine, but rather the fact that the reward is in the form of Steem Power which is vested for 2 years, which is still true with the new mining algorithm. Also, because the mining algorithm depends on the account name directly, others cannot steal a miner's found PoW even if they share the same active key at the time (this is better protection against PoW theft than the old algorithm). Finally, although there are no more secrets kept with PoWs in the new mining algorithm (which is now more similar to Bitcoin), the new mining algorithm does still intentionally depend on ECDSA to keep the advantages of GPU resistance (or alternatively benefiting the ecosystem as a whole when someone does build and release a GPU miner for Steem) that were discussed earlier.

Pseudocode of Steem's new mining algorithm

So, the new mining algorithm (as of hardfork v0.13) for Steem could be summarized with the following pseudocode:

1) d         = SHA256(miner_account_name || latest_block_id || nonce)

2) input     = SHA256(d)

3) sig       = ECDSA signature (in 65-byte format) of input using d (the private key) and a signing nonce which is deterministically derived from private key d and message hash input in the standard way (using RFC 6979)

4) sig_hash  = SHA256(sig)

5) pubkey    = Recover public key (33-byte format) corresponding to the private key that would have signed sig_hash with signature sig

6) work      = SHA256(input || pubkey)

work must be smaller than the target work at the time which corresponds to the mining difficulty (smaller target work value means higher mining difficulty)

How @supercomputing was able to dominate the mining queue and how the bug was fixed.