Fuzzy logic, fuzzy sets, fuzzy relations, fuzzy numbers, fuzzy arithmetic, fuzzy control system...
In this post we will talk about fuzziness - therefore let's first become acquainted with that concept. The term is closely related to two other terms: vague and uncertainty. Here is excerpt from Oxford English Dictionary.
fuzzy
- of, resembling, or covered with fuzz
- indistinct; unclear or distorted
- not clearly thought out or expressed
- (of the hair) tightly curled or very wavy
- Maths. of or relating to a form of set theory in which set membership depends on a likelihood function: fuzzy set; fuzzy logic
vague
- (of statements, meaning, etc.) not explicit; imprecise: vague promises
- not clearly perceptible or discernible; indistinct: a vague idea; a vague shape
- not clearly or definitely established or known: a vague rumour
- (of a person or his expression) demonstrating lack of precision or clear thinking; absent-minded; [C16: via French from Latin vagus wandering, of obscure origin]
uncertainty
- also called: uncertainness; the state or condition of being uncertain
- an uncertain matter, contingency, etc

Historical development of fuzzy logic can be followed from 1920's when Jan Łukasiewicz, Polish logician and philosopher who studied analytic philosophy and mathematical logic laid foundation of many-valued logic - a logic in which where not only truth and lie exist but also various levels of truthfulness of propositions. Families of many-valued logic are labeled with Ln hence we have:
- L2: truth values can be {0, 1} => classical logic
- L3: truth values can be {0, 1/2, 1},
- ...
- Ln: truth values can be {0, 1/n-1, 2/n-1, ..., n-2/n-1, 1}
- L∞: truth values can be from interval [0,1] ⊂ Q
- L1: truth values can be from interval [0,1] ⊂ R

The term vagueness was introduced by Bertrand Russell, English philosopher, logician, mathematician, historian and society critic, among other things known by Russel's Paradox which indicates flaws of classical logic.
Here's what it's all about: according to the crisp set theory, every collections that can be defined is a set. Let R be the set of all sets which don't contain itself as a member. Here is the paradox: if R contained itself as a member, then it would contradict the definition of that set, therefore that's impossible; on the other side, if that set does not contain itself as a member, then it is by the definition element of the set R which produces contradiction again.

This problem can be observed on a practical example: "In some village there exists a barber which shaves exclusively those people who don't shave themselves; who shaves the barber?"
If he is shaved by himself, then by the definition he is getting shaved at his own place, therefore he shaves himself. On the other side, if he shaves him self, then he is not getting shaved in his place, because he shaves only the people who doesn't shave themselves - and a paradox emerges. But Berdtrand Russell was mentioned only because of the term vagueness: here is the paradox known by the name Sorites' Paradox which illustrates this.

"We can all agree that 1,000,000 grains of sand creates a heap (as in large amount of something). If we remove one grain of sand, we still have a heap. How many grains of sand should we remove so that leftover is not a heap anymore?"

Max Black, English-American philosopher which left significant mark in the area of analytical philosophy, in 1937. has published an article: "Vagueness: An Exercise in logical Analysis", Philosophy of Science, Vol.4. 1937., which at that time did not gain attention of the wider scientific community. It seems that the world at that the time was not ready for these ideas.

Around thirty years later, 1965. polish Lotfi A. Zadeh, Iranian-Russian mathematician, electric engineer, scientist who researched the area of computing and artificial intelligence has published an article: "Fuzzy sets", Information and Control, Vol.8, No.4, pp. 338-353, June 1965." and with that article initiated and popularized research from areas of fuzzy logic and fuzzy sets. Here is how Zadeh has described the relation of classical and fuzzy logic:

"Classical logic is like a person who comes at a party wearing black suit, white starched shirt, shiny shoes etc. Fuzzy logic is like a person who is wearing informal clothes, jeans, t-shirt and sneakers. Through the history, that kind of informal dressing was considered unacceptable, today it is the opposite."
In continuation of this post we will talk about the crisp set theory and afterwards we'll define and take a closer look at the term of fuzzy set and its properties.
Classical sets
In crisp set theory some element either is or is not a member of the set. For example we have integers set, odd integers set, even integers set, prime numbers set etc. On the question is number 3 a member of the even integers set there are exactly two possible answers: "yes, it is" or "no, it is not". Taking into account characteristics of the numbers which are important for this classifications, and that is that the even numbers are the ones divisible by 2, we conclude that the right answer to the given question is "no, it does not", as 3 is not divisible by 2.
Generally crisp sets can be defined in several ways.
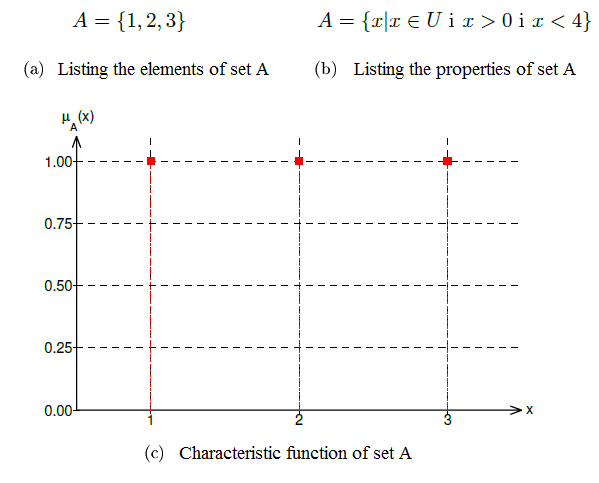
First step is to define universal set U, i.e. the domain out of which other sets can define its members. For example, let U be the set of all integer numbers. Second step is to define the sets of our interest.
One way is to list all the set elements. For example, we can say that set A is defined on the universal set U as a set of numbers {1, 2, 3}. This is possible while the number of members is finite, and in the practice there is an additional condition that the number should be relatively small (it is hard to list 10^40 elements).
Second way is to define the conditions that elements must satisfy to be a member of some set. For example, set A can be defined as following: it is the set of integer numbers greater than 0 and lesser than 4. In this way the set is unambiguously defined because the domain from which the elements are chosen (in this example, set of all integers) and the condition elements have to satisfy to join the set (greater than 0 and lesser than 4) is clearly defined.
The third way to defined a set is using the characteristic function μA : U -> {0,1}. Characteristic function μA is defined given the following:
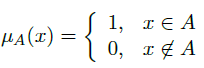
Therefore our set A can be defined by the following characteristic function:
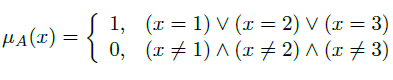
Fuzzy sets
Although the crisp sets are often used in practice, there is also a multitude of examples in which it is very hard to determine if given element belongs to the set or not, i.e. the examples in which the decision is not binary. Let's take for example the universal set of days in 2010. and try to build a set of sunny days. How do we decide which days belong to our set?

We can try this way: in our set belongs every day in which there were no clouds in the sky. But what's up with the days that had a small cloud on its sky for 5 minutes only? Are those members of our set? What if there was a cloud for 10 minutes? 15 minutes? 20 minutes?

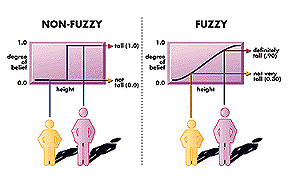
Let's look at another example. We will define the universal set whose members are all people living in New York. We want to determine which of those people belong to the set of tall people. How can we do this? If we would work with crisp sets, we would have to define a boundary height, and all the people who are tall at least that much would be its members.
Let's take for example that the boundary height is 180 cm. Then tall people set members would be the people with height equal or more than 180 cm. However, is this the good the way to build the tall people set?

Let's look at one trivial consequence of this kind of set creation: John Johnson who is 180 cm tall belongs to the set, but Michael Michaelson who is 179.98 cm tall does not. Hm, okay, we can move the limit to 178.98 cm so that Michael is also considered a member of tall people club. But here comes the new problem - Jamie Jameson's height is 179.97 cm and he does not belong to the set even though the difference in their height cannot be seen with a naked eye. Should we redefine the boundary again?
From this two examples we can clearly see that during the assessment of crisp sets a unpleasant problem arises - how to determine what belongs to the set, so that the boundary is clear, and what's more important, that the logic is common sense. Namely, saying the boundary is 180 cm, our statement would be clear, but we saw that this isn't the right way for sure, because it doesn't make sense. This kind of difficulties are one of the reasons for creation of fuzzy set theory which was developed by Lotfi A. Zadeh.
We saw that crisp sets can be described by characteristic functions which accepts element to be examined as input, and return 1 if element belongs or 0 if element does not belong to the set. Zadeh widened this concept in the following way: fuzzy set will be defined by the membership function which will accept element to be examined as input, and as output it will produce real number from interval [0,1] which will describe to what degree does that member belong to the fuzzy set.
Fundamental difference between crisp and fuzzy sets is that in crisp set an element either belong or does not belong to the set, whereby in fuzzy sets an element belongs to the set with a certain degree. It can clearly be seen that fuzzy sets are widening of the crisp sets, because if we limit the codomain of the fuzzy set membership function exclusively to values of 0 and 1, we will end up with the crisp set, that is the membership function will be degraded to characteristic function.
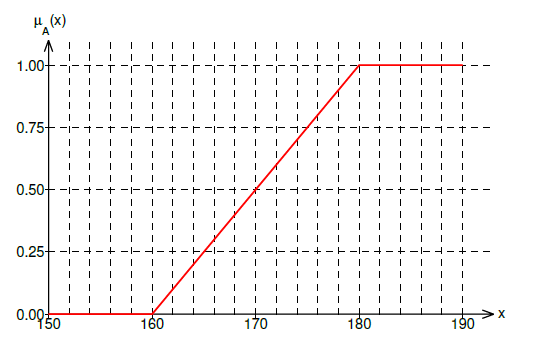
The way in which we will distribute the degrees of affiliation is up to us. We can for example linearly stretch it from the value 0 for the 160 cm height to value 1 for 180 cm height. That way a person with the height of 170 cm would belong to the set of tall people with the membership degree of 0.5, a person tall 175 cm would belong with the degree of 0.75, a person tall 179.98 cm would have the value of 0.999.
Or we could define it with the following characteristic function:
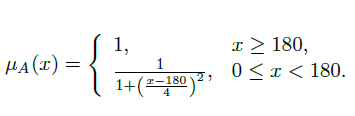
This will result in all people being members of the tall people set to some degree.
As the problem of choosing the appropriate membership functions occurs during the definition of every fuzzy set, there are some usual functions which are used often, which we'll take a look at in a moment. In addition it should be noted that the selection of the membership function is entirely subjective and contextually dependent, or as Zadeh had described it: "the exact values of the membership function in some context are not important, rather a mutual relation of values".
Characteristic forms of membership functions
Λ(lambda)-Function
If we want to define concepts like "numbers around 5", "speed around 40 mph" etc. we will need a fuzzy set whose membership function adopts value 1 right at the central element ("number 5", "40 mph speed") and moving away from it results in lower values.

Good candidate for that kind of membership functions is a Λ(lambda) function. It is defined by the 3 parameters.
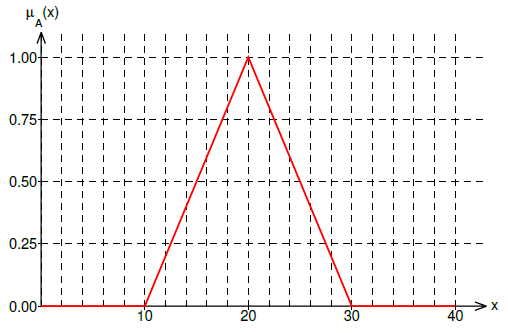
α=10, β=20 and γ=30
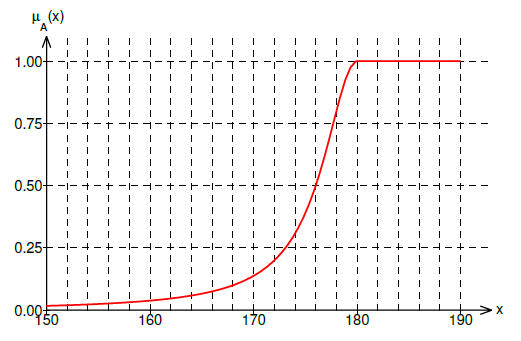
Γ(Gamma)-Function
For concepts like "high temperature", "tall people", "number of grains of sand which makes a heap", "number of guns which makes a well armed army" etc., Λ-function is not appropriate. In this situation we need membership function which has value 0 until some boundary element, then it starts to grow, and finally, for some element it reaches the value of 1.
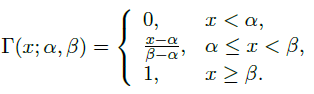
For this function a good candidate is a Γ-function. It is defined by 2 parameters.
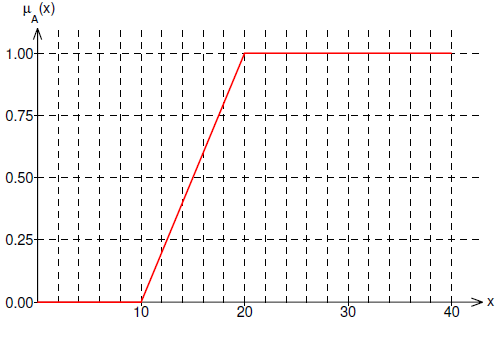
α=10, β=20
L-Function
If we want to define exactly the opposite from the previously mentioned concepts, for example. "low temperature", "short people", "number of grain sands that don't create heap", "low speed of wheel rotation" etc., we will need a function which returns a value of 1 for all the "small" elements, then it starts falling down and finally for some element and beyond it returns 0.
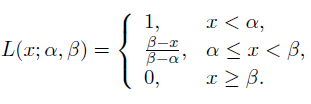
Good candidate which satisfies this conditions is a L-function. It is defined by 2 parameters.
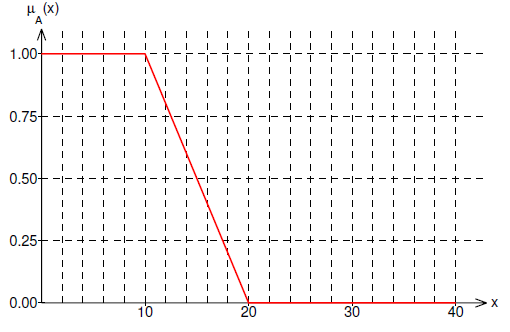
α=10, β=20
Π(pi)-Function
Finally, we must not forget about one more type of concepts: "number of grains of sand which creates a medium-sized heap", "number of guns that makes a medium armed army", "number of rain drops which moistens the land just enough" etc.
It is very similar to Λ-function but with one important distinction. In this concepts there is no central element which describes idea the best, rather there is a whole interval of elements which describe the concept well enough. It means that the membership function will return the value 1 on a defined central interval.
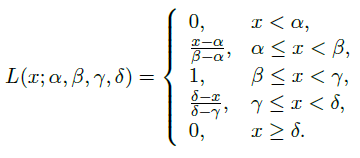
Good representative of this kind of membership functions is a Π-function. It is defined by 4 parameters.
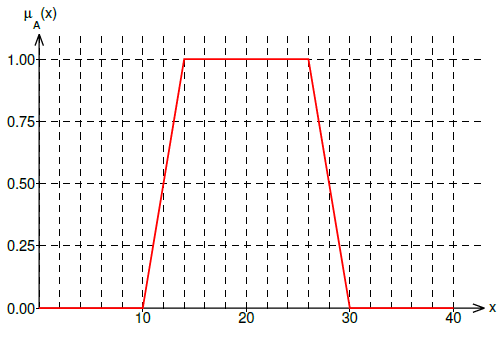
α=10, β=14, γ=26 and δ=30
Smooth functions
All the previously mentioned functions belong to the class of "partially linear functions". Fundamental advantage of this definitions is in simplicity and calculation speed. A complex mathematical tool is not needed neither are strong computer circuits for realization of those functions. Of course, except the good properties, these functions also have some properties making them less appropriate for some implementations.
For example, these functions don't satisfy derivability property in all points. Exactly at the crucial points derivation is not unambiguous. Because of it a new class of membership functions is developed, so called smooth functions.
All the functions mentioned previously have their equivalent in the class of the smooth functions. I will not provide additional explanations for those because everything mentioned for partially linear functions works for smooth functions as well. I'll only mention few, maybe you can recognize some: S-Function, Gauss Function, Sigmoid Function, π-Function, Exponential-like membership function etc.
Summary

Classical logic only permits conclusions which are either true or false. However, there are also propositions with variable answers, such as one might find when asking a group of people to identify a color. In such instances, the truth appears as the result of reasoning from inexact or partial knowledge in which the sampled answers are mapped on a spectrum.
Fuzzy logic is used in situations when binary decisions are not possible or they do not make sense.
It is essential part of today's computing science, used in areas ranging from control theory to artificial intelligence.

“As complexity rises, precise statements lose meaning and meaningful statements lose precision”
Lotfi A. Zadeh
If you provide feedback and show interest, I could provide the programmed solutions (probably coded in Java) which could help in the understanding of the topic.
Thank you for reading.