Our daily life is followed by the Gregorian calendar, a reform that was carried out in 1582. Many people think that a leap year is one that is divisible by 4 and that is all, but there is another part in the rule! if it is divisible by 100 but not by 400 then it is not a leap year. For instance, 2100 will not be a leap year despite being divisible by 4. In this post I will explain how they came to this conclusion and how it could have been better.

First let's look at some history!
There are many calendars that were created around the world (Persian, Hebrew, Mayan, Egyptian, Roman, ...), among them I will focus on one that evolved until today: The Roman calendar.
In the Roman calendar a year had exactly 365 days, starting from March and ending in February. But the calendar was always out of date, and the generals often used it in their favor and added days to their liking to adjust it.
Once Julius Caesar arrived, they studied what the problem was and the astronomer Sosigenes came to the conclusion that a year had 365 days plus 1/4 of a day! Therefore he decided to compensate it adding 1 day every 4 years, the leap year, and this day was added to February. This was the Julian calendar, which was introduced in 45 BC.
Years passed and in 325, at the Council of Nicaea, the church defined what was the calculation of the Easter Resurrection, the main holiday of Christianity. It must have been Sunday after the first full moon after the spring equinox, which in that year was dated March 21. This fact is very important because it comes to explain what happened next.
The Gregorian Calendar
If the spring equinox is an astronomical event that happens exactly once a year, everyone would expect it to always fall on March 21. However, this was not so. Year after year, and very slowly, this date was out of phase. Until in the sixteenth century (1200 years later!) There was a 10 day error, the spring equinox was dated March 11. This confused the church and much more if to this we add the lunar cycle, which is totally different, and was necessary to calculate the date of Easter.
At this moment comes the proposal of reform of Luis Lilio and that continued the outstanding Cristobal Clavio. They based on the Alfonsine Tables to say that the year had 365 days 5 hours 49 minutes and 16 seconds, that is, 365.242546 days. And therefore they proposed to remove 3 leap days every 400 years. Let's calculate how long the year lasts:
Every 400 years, there are 400/4=100 leap days, if we remove 3, then there are 97 leap days. Let x be the length of a year, then:
400x = 400(365) + 97 --> in 400 years there are 97 additional days
x = 365 + 97/400
x = 365.2425
And 365.2425 is quite close to the Alfonsine Tables. Finally this reform was introduced in the year 1582 by Pope Gregory XIII, and to correct the 10 days of delay they decided that in that year after October 4 would continue on October 15.
And this is the time frame we are currently governing. Every 4 years we have a leap, but, for example, between 2000 and 2400, 3 leap will be removed, which will be 2100, 2200 and 2300. As mentioned in the rule: leap years are divisible by 4, except divisible by 100 that are not divisible by 400.
... and could have been more accurate?
The answer is yes. For this we must return to the spring equinox and make a simple calculation.
Between 325 and 1582 there are 1257 years. If there are 10 days of error in 1257 years, then:
1 day of error every 125.7 years
2 days of error every 2x125.7 = 251.4 years
3 days of error every 3x125.7 = 377.1 years
4 days of error every 4x125.7 = 502.8 years
Look that 377.1 is near to 400, then if there are 3 days of error every 377 years, we can remove 3 leap days every 400 years and doing this the error is compensated. This is the Gregorian Calendar.
However, taking the following case we are closer: If every 502 years there is an error of 4 days, we can remove 4 leap days every 500 years to compensate! Do you notice that it is much closer? 500 is very close to 502, much more than 377 is from 400. Then it is better to take a reference of 500 years.
In this case we could say that the rule would be: Leap years are those divisible between 4, except those divisible by 100 that are not divisible by 500. Or in other words: divisible by 4, except those ending in 100, 200 , 300, 400, 600, 700, 800 and 900.
Now, let's calculate how long the year lasts:
Every 500 years, there are 500/4=125 leap days, if we remove 4, then there are 121 leap days. Being x the length of a year, then:
500x = 500(365) + 121
x = 365 + 121/500
x = 365.2420 days
The astronomers of that time were only fixed in the Alfonsine Tables. The problem is that these tables consist of observations made during 9 years, which may be little if you want to detail something that lags in a much longer time. However, this does not detract from their great merit, apart from the work they did to calculate the lunar cycles, which I have not addressed here.
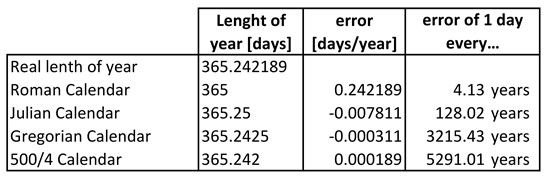
Finally, I want to summarize the accuracy of the calendars we mentioned. In our times we know with greater accuracy that a year has 365.242189 days. Let's take the Julian Calendar:
error = 365.242189 - 365.25 = -0.007811 days per year... this negative value indicates that the Julian Calendar counts too slow (we need to count more fast, then remove leaps). Seen in another way: 1/0.007811 = 128.02 years per day. Every 128 years there is one day late. The following table summarizes these calculations for the other calendars.
I hope you liked it. See you in the next post!
