A common misunderstanding, even among musicians who have not trained in Early Music, is the confusion between pitch, see our other post, and temperament. Pitch is where you put the 'A', in modern days it has stabilised around 440Hz or a touch higher, and there is a vocal group that touts the benefits for the 432Hz pitch. Pitch, we will address tomorrow in a new post.
However, temperament is not pitch. Temperament is the distribution of the octave among the semitones. In modern days, this has settled into what is known as equal temperament.
Quick primer on terms used
I am going to assume some musical and physics/mathematical knowledge, please ask in the comments if there is something that needs further explanation.
First term that needs to be explained is the idea of Hz. This is the frequency of (in this case) of a musical pitch, for this tuning article, we are only talking about pure tones and not the mix of frequencies that lead to the idea of "timbre".
Second term, cents, not SBD cents. 100 cents form a semitone in an equal tempered scale, this is done as a reference point and not because the equal tempered scale is the "best".
The Problem
The problem lies in the fact that we must divide the perfect octave into 12 semitones. There are many ways to achieve this, however, this leads to many different degrees of "in tune-ness" depending on how the semitones are distributed.
The most "in-tune" way of tuning a chord is with just intonation, this is otherwise known as pure intonation. This is essentially tuning the Octave, fifth and third according to the natural harmonic series that appears from any resonant system (pipes or strings). It is possible to do this for all the semitones, so we assign the values of pitch that would appear in the harmonic series to the semitones. To hear this, this article has audio examples. However, this "perfect" intonation in one key leads to some horrific out of tune-ness in pretty much every other key, getting worse the further you move away from the initial tuning key.
Another way to explain this, is that if you used perfect fifth and kept stacking them on top of each other, you should arrive back to the original note (albeit somewhat higher in pitch) after 12 fifths. You DON'T!
This situation was tolerable for music before the Renaissance period, when the music did not stray far from it's beginning key. It was also relatively tolerable for instruments that didn't have a fixed pitch (all non keyboard instruments).
Baroque solutions
Coming into the Baroque period, the diversity of keys and modulations into further afield keys highlighted this problem of "out of tune" keys.
There were broadly two camps that approached this problem.
The first camp sought to embrace these differences, to attribute different affects (emotions) to different keys. Thus the more in-tune a key, the more calming the affect. The more dissonant the key was, the more harsh the affect was. Thus, the idea that pieces written in different keys had different affect/character was born.
From this idea, attempts to spread the out of tune-ness was born. Temperaments like meatone and Werckmeister were devised to shift the "wolf" (the horrible out of tune interval) to lessen the out-of tune-ness of just intonation, whilst keeping as much as possible the pure intonation of the earlier temperaments.
The second camp sought to fix the "problem" and to try and devise a way of tuning the system equally. So, in effect distribute the ocvtave exactly evenly between the 12 semitones. Keep in mind that we didn't have electronic tuning machines, so this had to be done by ear. Read below about Equal tuning to understand why it didn't happen instantly!
From this idea, came the temperaments like Valotti. For his work ,"The Well Tempered Clavier", JS Bach lays out a tuning system that was encoded in the above scribble.
In practice, each keyboard player came up with their own solution to tuning their instruments. There were even extreme examples of using extra split keys (see the photo at the top of this section) to recreate the differences between the C# and D-flat and all the other enharmonic semitones. The method of tuning to each temperament by ear is a skill that is best left to a harpsichodist to explain!
Modern day Equal Temperament
Pretty much all Western music that you hear today (from 'normal' traditional Classical music right up to the latest rock/electronica) uses the Equal Temperament scale. This is the technique of distributing the octave evenly (according to the logarithmic scaling) between the semitones. The frequency ratio of an octave is 1:2. Thus each semitone has the ratio 1:12th root of 2 (roughly 1.05946). Needless to say, this is a bit tricky to do by ear and was the explanation why this was not immediately settled upon as a solution.
In a way it is the ideal compromise solution. No chord or key is "out of tune", however, no chord or key is "in tune". They are all equally mediocre. In many ways, this is a sad departure from the promise of music being the sonic description of emotion and character. To neuter one of the most fundamental aspects of our art into blandness was an unfortunate decision.
Please keep in mind this article is a simplification of the topic, and not a scholarly article. If you wish to learn more in depth, please leave a comment and I can point you to books and treatises that would be helpful.

Running an ensemble is a rewarding but time consuming job. Chasing after grants and sponsorship is the often overlooked but important aspect of a musician's life. Please visit our musicoin playlist. If our post has passed the reward period, please consider a donation or a delegation. We also accept tokens of support at the following addresses:
BTC
1Mwe6XaDcREa7o5RSLGoWfk9wSwGs6LkSA
LTC
LPcEtTsxMJykDeK713jsj3e2BsdVf32ix7
ETH
0x1bb1d830f66bdb74de45685a851c42b790587a52
Doge
DMJNS7jbNCgPdFdxgeFdEummFMmSQvAoK2
Musicoin
0x9c1fc741f0869115f8c683dc6967131ab1c40ebc
Smartcash tips accepted!

Our Musicoin artist page
Thanks for you support!
Please let any classical musicians or classical music lovers that you know to subscribe to @classical-music, and to start using the #classical-music hashtag, so we can try and grow our community! Join us at our Dischord: https://discord.gg/ppVmmgt




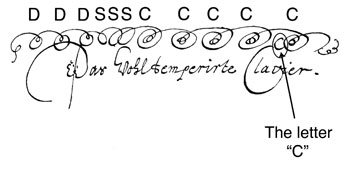

.png)