Dynamic Programming (DP) is one of the very important algorithm in Computer Science. Here is the simplest example of demonstrating the concept of DP if you want to tell you 5-year-old son.
Give 5 matches to your son, and ask: "How many matches do you have?"
-- The kid counts and says: Five.
Then, give one more match to your son and ask, how about now?
-- The kid says Six because he knows Five + One More equals Six...
The concept of DP is quite similar to this: breaking a problem into a smaller one + memorization of solutions to sub-problems.
Given a positive integer n, break it into the sum of at least two positive integers and maximize the product of those integers. Return the maximum product you can get. For example, given n = 2, return 1 (2 = 1 + 1); given n = 10, return 36 (10 = 3 + 3 + 4).
We can use Dynamic Programming (DP) to solve this problem. The puzzle does not ask you exactly how to break the integer. If we use f(n) to denote that the maximum product to break the integer n, then we have the following recurrence formula:
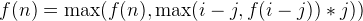for 1 <= j < i <= n
If we break the integer i-j, the intermediate result is f(i-j) otherwise we have to check if we break i into i-j and j. The time complexity is O(n^2) and the space complexity is O(n).
动态规化 (Dynamic Programming) 是个计算机领域里很重要的算法，我在高中参加过三次信息学奥林匹克竞赛 (ACM)，每年必有一题用动归(DP)来解答. 动态规化其实就是 把问题分解成子问题+记忆子问题求解的一个过程。
你如何教你的孩子DP是什么呢？
比如：你给你的孩子5根火柴，你的孩子数了数然后说有5根。然后你再给你的孩子1根火柴然后问一共有多少根，这时候你的孩子会马上说出6根，因为他知道已经有5根了，再加上1根就是6根。
原理就是：把问题分析成更小的问题，并分而求之，子问题的解会被保存下来这样在求解更大的问题的时候就不需要再重新把中间结果再算一遍了。
动态规化的解法经常是较优的一种解法，我们来看这么一道面试题：
给定一个正整数，将它拆分成至少两个正整数，求出这些正整数的最大乘积。比如 整数2，可以拆分成1+1， 乘积是1，当输入是10，需要分解成3+3+4，这样所得的最大乘积是36。
你会怎么解？暴力搜索？这种解法不好写，而且时间复杂度也大。可以用回溯+剪枝，但时间复杂度也相对较大，特别是当N较大的时候也会时间太久Time Exceeded.
动规解答这题就较为简单。这题并没有让你详细写出怎么拆分的方案，只需要解出最大的乘积即可。所以我们有以下的方案：
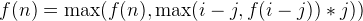其中 1 <= j < i <= n
我们用 f(n) 来表示整数N拆分后的最大乘积，那么我们当我们把整数 i 分解成两部分 i - j 和 j, 那么 最大乘积是 f(i - j) * j 和 (i - j) * j 的较大值。我们需要O(N^2)循环来寻求最优拆分法。
动规在计算 f(n) 的时候会需要取决于 f(i - j)的值，这时候每个f(m) 的值就会被保存起来以供之后迭代使用。这也是一个记忆的过程。以下实现就相对简单好理解。空间复杂度也是O(N^2)
If we break the integer i-j, the intermediate result is f(i-j) otherwise we have to check if we break i into i-j and j. The time complexity is O(n^2) and the space complexity is O(n).
class Solution {
public:
int integerBreak(int n) {
vector<int> f(n + 1, 0);
f[1] = 0;
f[2] = 1;
for (int i = 2; i < n + 1; i ++) {
for (int j = 1; j < i; j ++) {
f[i] = max(f[i], max(i - j, f[i - j]) * j);
}
}
return f[n];
}
};
Thank you for reading my post, feel free to FOLLOW and Upvote @justyy which motivates me to create more quality posts.
非常感谢阅读, 欢迎FOLLOW和Upvote @justyy 能激励我创作更多更好的内容.
近期热贴 Recent Popular Posts
- How to Claim BCC? BTC Hard-Fork via C program (Linux) 小白教程: 怎么领取 BCC (Bitcoin Cash) ?
- I wrote a Chinese Chess Program 软件分享: 智慧中国象棋 (Chinese Chess)
- Planning Cards – Agile Poker Game! 敏捷开发扑克游戏
- Software Engineer Interview Question - How to Check Valid Sudoku in C/C++? 软件工程师面试技巧之 如何检查数独的有效性
- Google Interview Question – Print Message - 去年 Google 的面试题 - 打印消息
- Software Engineer Interview Tips - Using Hashtable to Reduce Runtime Complexity 软件工程师面试技巧之 使用哈希表降复杂度
- Technology-driven or Business-model-driven? 技术优先还是商业模式优先 – 献给在30多岁还在写代码的朋友们
- 记录那些值得回忆的精彩瞬间