在之前的文章中,学习了这些东西:
尤其是通过最后一篇文章的学习,已经可以生成比特币的私钥,并可以将生成的私钥导入到 blockchain.info 在线钱包,并由此得到比特币地址。通过从blockchain.info 钱包导出私钥与我们获得的私钥对比,我们得知并基本掌握了私钥的几种表示方法。
- HEX
- Base58
- WIF
- WIF-Compressed
椭圆曲线与公钥
提到私钥我们常常提到公钥,他们是成对出现的。
公钥是从私钥通过椭圆曲线运算计算得来的,这个过程是不可逆的。亦即通过私钥可以算出公钥,反之则不行。

( Source: 《Mastering Bitcoin》)
别问我啥意思,不懂,就是看着挺好看是不?
比特币使用NIST(National Institute of Standards and Technology)确定的secp256k1标准中定义的椭圆曲线以及一组数学常量。
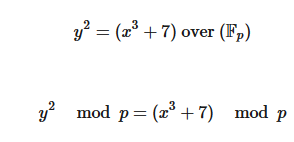
( Source: 《Mastering Bitcoin》)
看了一下椭圆曲线的讲解,一头雾水,看来凭我的智商是学不明白了,交给数学家们去研究好了!
我关心的是,如何从私钥到公钥,研究了半天,原来很简单,就是一个公式:
K=k∗G
其中小k是我们的私钥,G是生成点,K是结果亦即公钥是曲线上的另外一个点。
因为生成点对所有的比特币用户都是相同的,所以同一个私钥k乘以生成点G,总会得到相同的公钥K。所以从k到K是确定的,并且只能单向运算。这就是为何比特币地址(由公钥生成)可以告诉任何人不用担心泄露私钥。
Steem 官方Python 库中的实现
secret = unhexlify(repr(self._wif))
order = ecdsa.SigningKey.from_string(secret, curve=ecdsa.SECP256k1).curve.generator.order()
p = ecdsa.SigningKey.from_string(secret, curve=ecdsa.SECP256k1).verifying_key.pubkey.point
x_str = ecdsa.util.number_to_string(p.x(), order)
y_str = ecdsa.util.number_to_string(p.y(), order)
compressed = hexlify(bytes(chr(2 + (p.y() & 1)), 'ascii') + x_str).decode('ascii')
uncompressed = hexlify(bytes(chr(4), 'ascii') + x_str + y_str).decode('ascii')
其中repr(self._wif)得到的是HEX形式表示的私钥
导入我们之前生成的私钥试试看:
a591a6d40bf420404a011733cfb7b190d62c65bf0bcda32b57b277d9ad9f146e
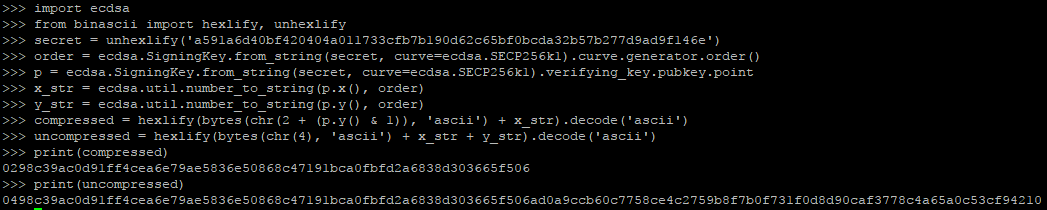
我们也会生成公钥了!!!
神马椭圆曲线,神马方程之类的,统统丢一边去吧
作为常年CTRL+C, CTRL+V变成的猿类,不需要了解太高深的数学姿势!
(PS: 数学家们是最值得尊重的了,没有他们的辛苦耕耘,我们就没有这么多好用的数学工具)
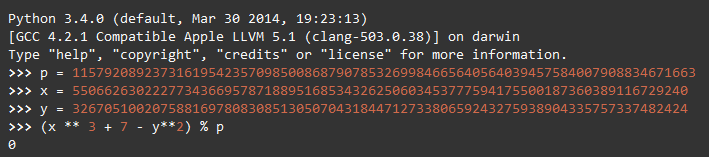
《Mastering Bitcoin》中有一个例子,验证点P在secp256k1定义的椭圆曲线上。
我们也来验证一下我们的生成的点P符不符合要求。

完美
示例代码
本文中所使用的代码如下:
感兴趣的朋友可以使用自己的私钥试试来生成公钥玩。
import ecdsa
from binascii import hexlify, unhexlify
secret = unhexlify('a591a6d40bf420404a011733cfb7b190d62c65bf0bcda32b57b277d9ad9f146e')
order = ecdsa.SigningKey.from_string(secret, curve=ecdsa.SECP256k1).curve.generator.order()
p = ecdsa.SigningKey.from_string(secret, curve=ecdsa.SECP256k1).verifying_key.pubkey.point
x_str = ecdsa.util.number_to_string(p.x(), order)
y_str = ecdsa.util.number_to_string(p.y(), order)
compressed = hexlify(bytes(chr(2 + (p.y() & 1)), 'ascii') + x_str).decode('ascii')
uncompressed = hexlify(bytes(chr(4), 'ascii') + x_str + y_str).decode('ascii')
p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
x = int(hexlify(x_str).decode('ascii'), 16)
y = int(hexlify(y_str).decode('ascii'), 16)
(x ** 3 + 7 - y**2) % p
总结
- 公钥(K)可以通过椭圆曲线运算由私钥(k)计算得出
- 私钥(k)到公钥(K)计算公式: K=k∗G
- 生成过程使用secp256k1标准中定义的椭圆曲线以及一组数学常量
- 从私钥(k)到公钥(K)结果是确定的,并且只能单向运算
- 使用Python的ecdsa库,可以轻松实现私钥(k)到公钥(K)的计算
今天就探索到这里。
免责声明,本文为个人理解,示例仅供参考
因使用文中代码造成的损失,概不负责!
