#1 深度学习笔记 I – 卷积神经网络的直观解释 A - 整体结构
#2 深度学习笔记 II – 卷积神经网络的直观解释 B - Convolution & Pooling Step
#3 深度学习笔记 III – 卷积神经网络的直观解释 C - Introducing Non Linearity & Fully Connected
之前的笔记中记录了卷积神经网络中的主要操作步骤,在第三篇笔记中记录全连接层的概念的时候觉得非常唐突,因为完全没有记录什么是感知器,什么是多层感知器。这一次的笔记用来记录多层感知器,以及前馈神经网络和反向传播学习的过程。
单一神经元 【A Single Neuron】
人工神经网络(ANN)这种计算模型是受到人脑处理信息时用到的生物神经网络的启发而提出的。神经网络中的基本计算单位是神经元(Neuron),可以称为节点(Node)或单位(Unit)。 每一个神经元从其他神经元或者外部环境接收输入信息,经过计算输出一个结果。每一个输入值都有一个对应的权重值(Weight),神经元通过定义的数学公式(例如下图中所示)计算出输入值的加权和(Weighted sum)。
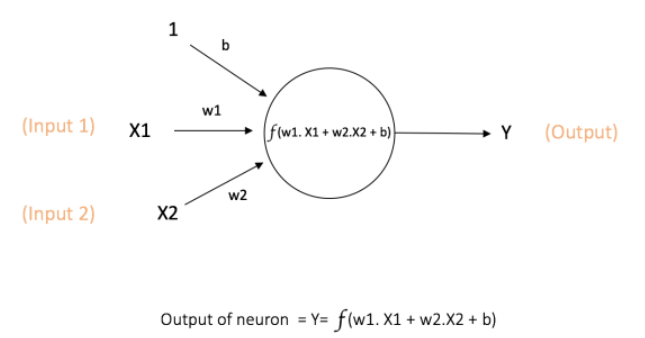
图中的神经元读入输入值X1和X2,每一条相连的边(Edge)表示与输入相关联的权重值w1和w2。 此外还有另一个输入值1,其权重为b(称为bias)与其相关联(这个bias需要单独一篇笔记记录)。
神经元通过图中的公式f()计算出输出Y的值。函数f()是非线性的,称为激活函数(咦?这个激活函数和ReLU是一回事吗?ReLU操作不是一般都在卷积操作之后Pooling操作之前吗?)。 激活函数的功能是将非线性引入神经元计算的结果,因为大多数现实世界的数据是非线性的,我们希望神经元学习这些非线性特性。
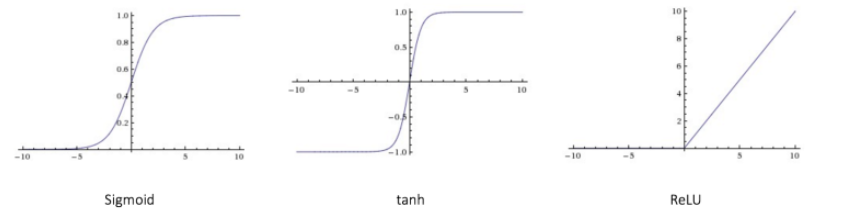
常用的激活函数已经在上一篇中记录,三种常用的激活函数在下图中列出。
Sigmoid: σ(x) = 1 / (1 + exp(−x))
tanh: tanh(x) = 2σ(2x) − 1
ReLU: f(x) = max(0, x)
关于Bisa的重要性,这篇文章Role of Bias in Neural Networks介绍的不错,下次再详细记录。
Importance of Bias: The main function of Bias is to provide every node with a trainable constant value (in addition to the normal inputs that the node receives).
前馈神经网络【Feedforward Neural Network】
前馈神经网络是第一种也是最简单的人造神经网络。 它包含多个排列成层(Layers)的神经元(节点)。 来自相邻层的节点之间互相连接(Connection or Edge), 所有的这些连接都具有与它们相关的权重(Weight)。
一个前馈神经网络的例子
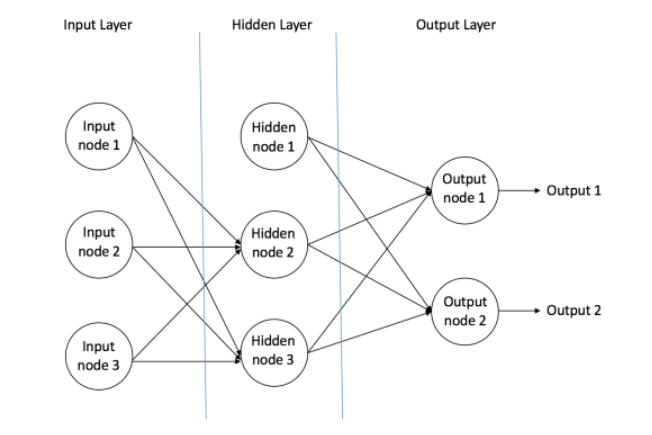
一个前馈神经网络可以通常包括三种不同的节点(Nodes):
输入节点 - 输入节点从外部得到输入信息,所以称为“输入层”(Input Layer)。 任何输入节点不执行计算,它们只将信息传递给隐藏层节点。
隐藏节点 - 隐藏节点与外界无直接联系(因此名称为“隐藏节点”)。 它们执行计算并将信息从输入节点传送到输出节点。 隐藏节点的集合形成“隐藏层”(Hidden Layer)。 前馈网络只能有一个输入层和一个输出层,但它可以有零个或多个隐藏层。
输出节点 - 输出节点统称为“输出层”(Output Layer),负责从把网络计算出的结果传递给外部。
在前馈网络中,信息仅在一个方向上移动,从输入层向前移动,通过隐藏层(如果有的话)到输出层。 网络中没有循环。依据神经网络中有没有隐藏层,可以将前馈神经网络分为两类:Single Layer Perceptron 和 Multi Layer Perceptron。
多层感知器【Multi Layer Perceptron】
多层感知器(MLP)包含一个或多个隐藏层(除了一个输入层和一个输出层之外)。 单层感知器只能学习线性函数,但多层感知器也可以学习非线性函数(单层如何学习线性的?)。
下图中是一个多层感知器。如上面所记录的,三个层,连接的Edge都有对应的weight值。给定一组特征X =(x1,x2,...)和目标y,多层感知器可以学习特征和目标之间的关系,用于分类。
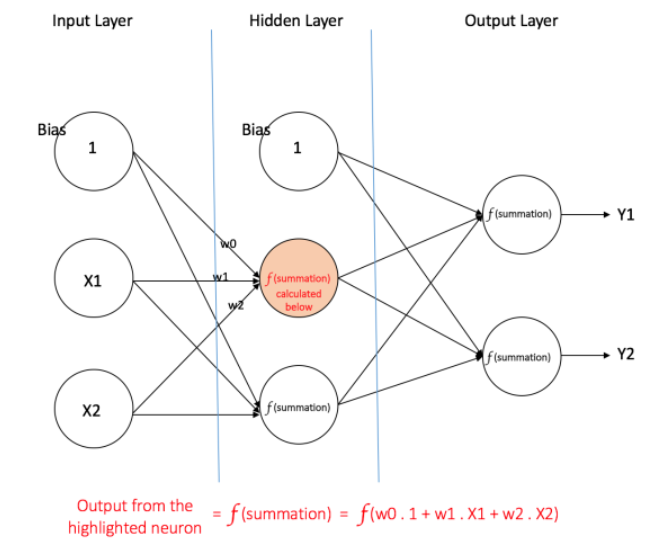
这里可以举个例子,看看神经网络是如何工作的。 两个输入列显示学生学习的小时数和学生获得的中期成绩。 最终结果列可以有两个值1或0,表示学生是否在最终考核时通过。 例如如果学生学习了35个小时,在中期考核时获得了67分,他/她会通过最后的期末考核。
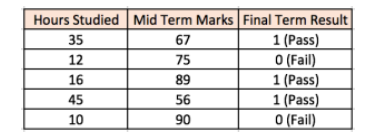
现在,假设想预测一个学习25小时并在中期考核得到70分的学生是否会通过最后的考核。

这是一个二分类问题,其中多层感知器可以从给定的示例(训练数据)中学习,并给出新的数据的预测。 下面记录多层感知器是如何学习这种关系的。
反向传播学习【Training our MLP: The Back-Propagation Algorithm】
具体的学习算法要接下来专门用一篇来记录。多层感知器学习的过程使用反向传播算法。 这篇文章How do you explain back propagation algorithm to a beginner in neural network?介绍的非常好。
Backward Propagation of Errors, often abbreviated as BackProp is one of the several ways in which an artificial neural network (ANN) can be trained. It is a supervised training scheme, which means, it learns from labeled training data (there is a supervisor, to guide its learning).
To put in simple terms, BackProp is like “learning from mistakes“. The supervisor corrects the ANN whenever it makes mistakes.
An ANN consists of nodes in different layers; input layer, intermediate hidden layer(s) and the output layer. The connections between nodes of adjacent layers have “weights” associated with them. The goal of learning is to assign correct weights for these edges. Given an input vector, these weights determine what the output vector is.
In supervised learning, the training set is labeled. This means, for some given inputs, we know the desired/expected output (label).
BackProp Algorithm:
Initially all the edge weights are randomly assigned. For every input in the training dataset, the ANN is activated and its output is observed. This output is compared with the desired output that we already know, and the error is “propagated” back to the previous layer. This error is noted and the weights are “adjusted” accordingly. This process is repeated until the output error is below a predetermined threshold.
Once the above algorithm terminates, we have a “learned” ANN which, we consider is ready to work with “new” inputs. This ANN is said to have learned from several examples (labeled data) and from its mistakes (error propagation).
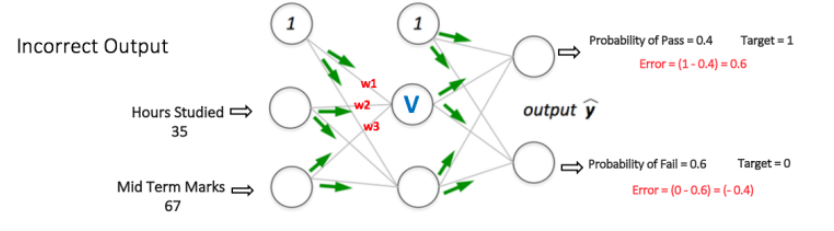
如下图中所表示的,神经网络有两个节点在输入层(除了Bias节点),它们对应“学习小时”和“中期成绩”。 它还具有一个带有两个节点(除了Bias节点之外)的隐藏层。 输出层也有两个节点,第一个节点输出“Pass”的概率,另一个节点输出“Fail”的概率。
前一篇文章,已经记录在输出层通常采用Softmax classifier用来归类以保证左右可能性的总和为1。所以这意味着:
第一步: Forward Propagation
网络中的所有权重值被随机分配。然后网络将第一个训练示例作为输入(对于输入35和67,通过的概率为1)这有有一个概念之前没提到,!监督学习!唉,随后记录。
输入节点值= [35,67]
输出节点值(目标)= [1,0]
那么节点V输出可以通过下面的公式计算(f是一个激活函数,如sigmoid或ReLU):
类似地,还要计算隐层中另一节点的输出。 隐层中的两个节点的输出充当输出层中两个节点的输入。 下一步能够计算输出层中两个节点的输出概率。
第二步: Back Propagation and Weight Updation
这一步需要单独一篇记录。主要操作就是通过已知的结果[1,0]和第一步中得到的结果计算出误差,然后进行反向推理不断的更新权重值(Weight),最终得到的结果和目标在很小的误差范围内。
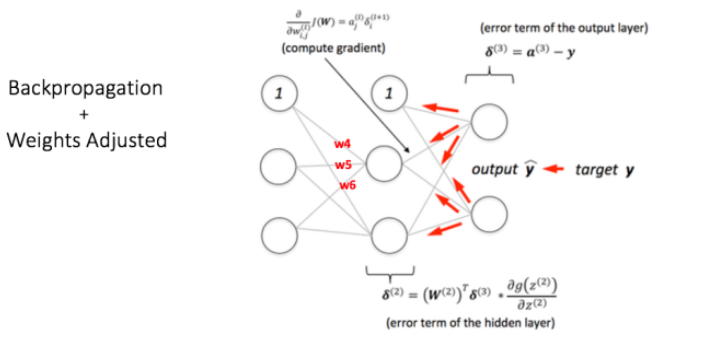
使用不同的训练数据重复上面两步操作,得到了合适的权重值,现在再给网络一个未知结果的输入值,网络将预测出这个学生能不能通过最终的考核。
这里省掉了反向传播算法的细节,会找一篇单独记录,这其中有几个英语词还是没找到好的翻译,例如Gradient Descent。
This post was originally inspired from A Quick Introduction to Neural Networks by Ujjwalkarn, I got the permission from original author by e-mail let me use it. All images used in this post belong to their respective authors.
在这个秋天,为自己的学习过程记录。
Reference
[1] https://ujjwalkarn.me/2016/08/09/quick-intro-neural-networks/
谢谢阅读 !
Please feel free to upvote, comment and follow me @victory622
