Mathematics × Programming Competition #6
Announcement of Answer and Winners
Announcement of Answer and Winners

For Chinese version please scroll to the bottom. 中文版請見文末。
Question
Given that x is a square number and p is a prime number, and they satisfy the equation x = 1000000007p + 1. Find the sum of all possible values of p.
Answer: 1000000009
Mathematical approach
Since x is a square number, we let x = n2, where n is a positive integer. Now we have
It is easy to check that 1000000007 is a prime number either by writing a program or using some online tools. Therefore there are only two possibilities:
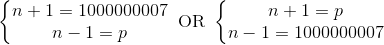
We have p = 1000000005 or 1000000009, but only 1000000009 is a prime, so our answer is 1000000009.
Programming approach
It is not quite possible to solve this problem directly by brute force programming, as the question gives a very large number 1000000007, and also asked for the sum of possible values (though there is actually only one possible value :p). However even if you are not able to think of the mathematical solution as shown above, you may still have a chance to find out the answer. Let me show you how:-
- You may think that there must be something special with the number 1000000007. Just use some online tools to analyze this number and you will find that it is a prime.
- However the number is too large! Let's try to replace the number by some smaller primes, such as 23, 29, 31, ...
- Write a program to search for possible values of p that fits our equation. There is no upper bound for the value of p so you can let the program run for several minutes for each case and then stops it.
- You should observe that the number of possible values of p in each case is either p - 2 or p + 2. Now we have found out the key without the use of mathematical skills!
Winners
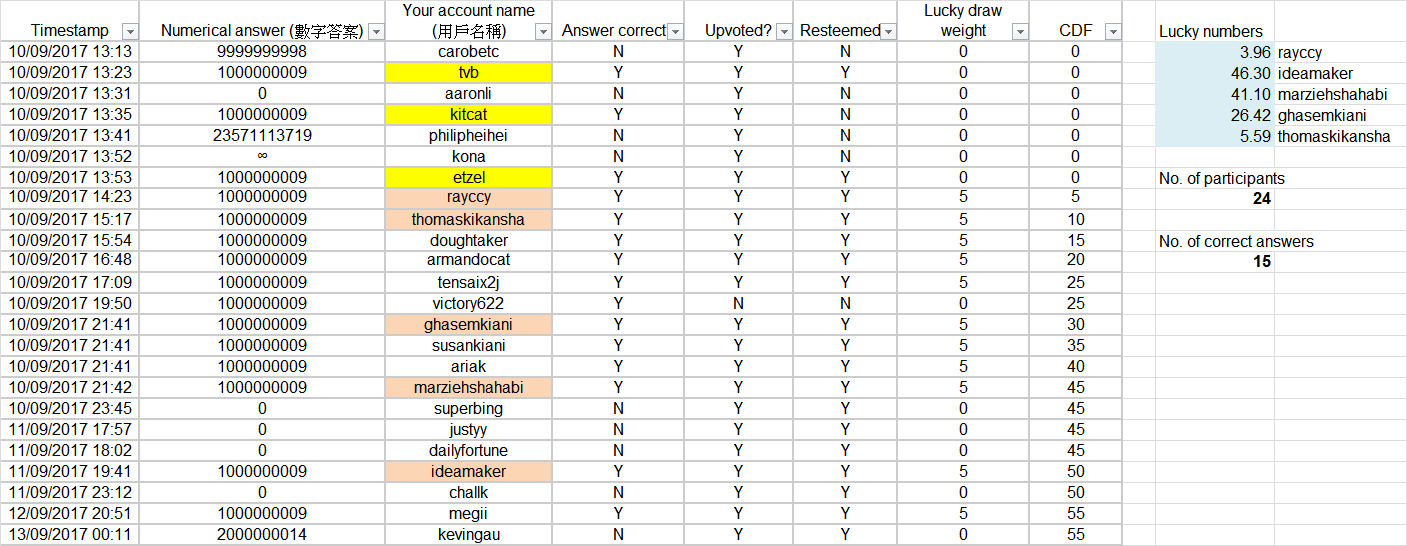
Among 24 participants, there are 15 people who got the correct answers. Thank you for your participation!
@carobetc @tvb @aaronli @kitcat @philipheihei @kona @etzel @rayccy @thomaskikansha @doughtaker @armandocat @tensaix2j @victory622 @ghasemkiani @susankiani @ariak @marziehshahabi @superbing @justyy @dailyfortune @ideamaker @challk @megii @kevingau
SBD payout of the the question post = 45.638 SBD
Besides, @steemstem has generously sponsored 7.5 SP, 5 SP and 2.5 SP for the first, second and third prizes!
The winners and prizes are tabulated below:
| Winner | Prize | SBD |
|---|---|---|
| @tvb | First prize | 45.638 / 8 = 5.704 SBD + 7.5 SP |
| @kitcat | Second prize | 45.638 / 8 = 5.704 SBD + 5 SP |
| @etzel | Third prize | 45.638 / 8 = 5.704 SBD + 2.5 SP |
| @rayccy | Consolation prize | 45.638 / 8 = 5.704 SBD |
| @ideamaker | Consolation prize | 45.638 / 8 = 5.704 SBD |
| @marziehshahabi | Consolation prize | 45.638 / 8 = 5.704 SBD |
| @ghasemkiani | Consolation prize | 45.638 / 8 = 5.704 SBD |
| @thomaskikansha | Consolation prize | 45.638 / 8 = 5.704 SBD |
Congratulations to the winners!

The steemSTEM project (@steemstem) is a community-supported project aiming to increase the quality and the visibility of STEM (STEM is the acronym for Science, Technology, Engineering and Mathematics) articles on Steemit. Please support steemSTEM by following @steemstem and joining the chat channel. You can also consider joining a private curation trail to further support steemSTEM by asking about it in the chat channel. In order to further promote the use of the chat channel, I will stop announcing the time of next competition via a post. Instead I will announce the time in advance in the chat channel!
數學 × 程式編寫比賽 (第六回)
答案及得獎名單公佈
答案及得獎名單公佈

問題
已知 x 為平方數,而 p 為質數,且符合公式 x = 1000000007p + 1。求 p 所有可能值之和。
答案: 1000000009
數學方法
由於 x 是一個平方數,我們設 x = n 2 ,其中n為正整數。現在我們有
通過編寫程序或使用一些在線工具,很容易得知1000000007是一個質數。因此,只有以下兩種可能性:
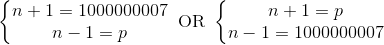
因此可得p = 1000000005或1000000009,但只有1000000009是質數,所以答案是1000000009。
編程方法
由於此問題包含非常大的數字1000000007,並且要求找出可能值的總和(儘管實際上只有一個可能值 :p),故並不太可能通過編程來暴力解決這個問題。然而,即使你不能想到數學解決的方法,你仍然有機會找出答案的 :)
- 你可能會覺得1000000007這個數字必定有其獨特之處。只需使用一些在線工具來分析這個數字,你會發現它是一個質數。
- 但是數值太大了!我們試著用一些較小的質數來代替這個數字,比如23、29、31...
- 編寫一個程序來搜索符合我們公式的 p 的可能值。 p 的值沒有上限,所以你可以讓程序為每個情況運行幾分鐘,待程序似乎沒有再找到新的可能值便終止。
- 你應該注意到,每種情況下 p 的可能值的數量只可能是 p - 2 或 p + 2。現在我們在沒有使用任何數學技能下已發現了題目的關鍵!
得獎者
在24個參加者之中,有15人答對。多謝大家的熱烈參與!
@carobetc @tvb @aaronli @kitcat @philipheihei @kona @etzel @rayccy @thomaskikansha @doughtaker @armandocat @tensaix2j @victory622 @ghasemkiani @susankiani @ariak @marziehshahabi @superbing @justyy @dailyfortune @ideamaker @challk @megii @kevingau
比賽題目帖文的SBD收入 = 45.638 SBD
另外,@steemstem 慷慨贊助了7.5 SP、5 SP以及2.5 SP予是次比賽的第一、二及三等獎!

下表顯示得獎者及其所得獎金:
| 得獎者 | 獎項 | SBD |
|---|---|---|
| @tvb | 一等獎 | 45.638 / 8 = 5.704 SBD + 7.5 SP |
| @kitcat | 二等獎 | 45.638 / 8 = 5.704 SBD + 5 SP |
| @etzel | 三等獎 | 45.638 / 8 = 5.704 SBD + 2.5 SP |
| @rayccy | 安慰獎 | 45.638 / 8 = 5.704 SBD |
| @ideamaker | 安慰獎 | 45.638 / 8 = 5.704 SBD |
| @marziehshahabi | 安慰獎 | 45.638 / 8 = 5.704 SBD |
| @ghasemkiani | 安慰獎 | 45.638 / 8 = 5.704 SBD |
| @thomaskikansha | 安慰獎 | 45.638 / 8 = 5.704 SBD |
恭喜所有得獎者!

steemSTEM(@steemstem)是一個由steemit社群支持的項目,旨在宣傳STEM(STEM是科學,技術,工程和數學的首字母縮略詞)。 請追蹤 @steemSTEM 以及加入聊天頻道來支持steemSTEM。你還可以透過加入自動點讚系統來在為了進一步支持steemSTEM,詳情請在聊天頻道內向負責人士查詢。為了推廣聊天頻道的使用,我將不再透過發文來宣布下一場比賽的時間,我會在聊天頻道中提前公佈比賽時間。
