(For anybody who missed it, here is Part 1)
Today we’re going to talk about Beauty Contests.

<Audience: “Get off the stage, @biophil! You said we were going to talk about Steem!”>
Easy there! Don’t worry - we’re getting to it. We’re going to be building up the groundwork nice and gently. There is method to the madness! Remember, this is game theory! In game theory, we give a cute name to all of our abstractions - and “beauty contest” is game-theory-speak for an important aspect of Steem: paying people to vote on stuff.
The story goes something like this: a newspaper wants to run a beauty contest. They’ll print the picture of 100 people, and then ask readers to mail in their choice for the most beautiful person. The question is this: how should the newspaper incentivize their readers to vote on the person they think is the most beautiful? (Anybody see the connection to Steem yet?)
The first incentive they consider is this: Pay people a flat $10 for submitting a vote. Consider the position of the voter: you get paid $10, regardless of who you vote for. Should you go through the trouble to look at all the photos and find the most beautiful one? Or should you just pick the first entry and pocket the $10?
Let’s introduce a bit of math, just to get our feet wet. We’ll do this in a totally abstract way. Let’s say we have the following components:
- n: number of contest entrants (100 in our example)
- p: amount you get paid for a vote ($10 in our example)
- t(k): how much time it takes a voter to search through k entries to find the most beautiful. Maybe we don’t know exactly what this function looks like, but we'll assume that the bigger k is, the bigger t(k) is (in math-speak we say the function t is monotone-increasing). This makes sense because the longer a list is, the more time it takes to search through it.
We’ll model the choice of a voter like this: the voter picks a number k between 1 and n, searches through the first k contest entries, and then votes on the most beautiful of those. If voter i chooses 1, that means they just vote on the first entrant. If voter i chooses 2, that means they look at the first 2 entrants and pick their favorite from those two; it "costs" them t(2) units of time to do this. And so on - all the way up to n. So the utility that voter i experiences for choosing to search through k entries is given by their utility function (or payoff function):
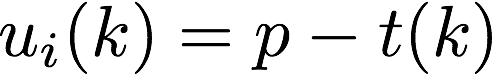
It’s just the payment p, minus the time it took the voter to search through k entries. Now, note that this isn’t really a game - the payoff of voter i only depends on i’s choice; there isn’t any strategic interdependence. But that’s ok, we can still find the k that maximizes the voter’s reward, and it’s very simple. The rational (that is, payoff-maximizing) choice in this setting is:
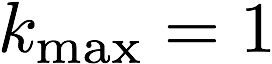
That is, each player should just pick the first contest entry. This is because it takes time to find the actual winner, and voters are not being compensated for this lost time, so we should not expect them to put any effort into doing what we’re asking them to do.
Moral of the story: If you pay people to vote and the payment is not correlated to the quality of their vote, don’t expect their votes to be meaningful.
What does any of this have to do with Steem?
If you haven’t noticed yet, Steem is a beauty contest. We’re paying people to find quality content, and we need to make sure that the voting incentives are supporting desirable behavior. In this case, we’ve ruled out the strategy of simply paying people a flat fee for voting. Fortunately, the devs also knew that this was a bad strategy. It’s pretty obviously a bad strategy - right? If we just paid people a flat fee for every vote, we’d see utter vote-vomit: people would just vote for everything, and their votes wouldn’t convey any useful information.
Next time, we’ll look at a slightly-more-complicated incentive mechanism that looks a bit more like how Steem works: pay people who vote for winners. It turns out that economists have been discussing that particular problem for over 80 years - in fact, it’s called a “Keynesian Beauty Contest.” Yes, that Keynes.
<Audience: "What?? That's it? You haven't told me anything even remotely surprising! I thought game theory was supposed to be surprising!">
Look - it's all about baby steps. We'll get there! But we have to walk before we can run.
One final note: The utility function I proposed above is about as simple as it can get. You can always add more layers of complexity. For example, here, it might be interesting to consider the fact that some people (maybe many people?) actually want to vote for the most beautiful; in other words, they’ll enjoy the process of searching through a bunch of entries. Modeling this can take different forms, but the simplest way would just be to give each person an individualized t(k) function, and let some people’s t(k) be decreasing in k; this would model the phenomenon that the more entries the person searches through, the happier they are.
