In den Kommentaren des letzten Beitrags aus #fotolern kam der Wunsch auf noch etwas über die "Hyperfokale Distanz" zu schreiben. Da ich mich vor ein paar Tagen ein bisschen belesen habe und 1-2 Videos dazu gesehen habe versuche ich mich mal daran. Bitte korrigiert mich wenn ich Blödsinn erzähle 😬 Übrigens es geht hier um Hyperfokal in der Fotografie, nicht um einen Krankheitsherd.
Hyperfokal (Hyperfocal) Was ist das
1. Wortbedeutung
Hyper kommt aus dem Griechischen und bedeutet "über" im Sinne von "mehr", "übertrieben" usw. Hypertonie - Bluthochdruck, Hyperglykämie - erhöhter Blutzucker, Hypes Hypes - Scooter
Fokal bedeutet auf den Brennpunkt bezogen, den Fokus betreffend.
Hyperfokal bedeutet praktisch "mehr Fokus" im Sinne von mehr als ein Fokuspunkt.
2. Was bedeutet Hyperfokal in der Praxis
Wenn man in der Fotografie von der Hyperfokalen Distanz spricht bedeutet es das man je nach Kamera, Objektiv, Brennweite und Blende einen Punkt in der Distanz hat auf dem der Fokus liegt und das Objekt scharf ist sowie die Objekte die eine bestimmte Distanz dahinter liegen.
Hört sich kompliziert an? Stimmt, ist es aber gar nicht. Praktisches Beispiel:
Bei meiner Sony Alpha 6000 liegt die Hyperfokale Distanz bei 50mm Brennweite und Blendezahl 5.6 von 11.19m bis 22.37m. Davon nehme ich die Hälfte - also 5.59m plus meine 11.19m = 16.78m diese 16.78m wähle ich als Abstand zu meinem fokussierten Objekt und Tadaa ich hab ein Bild mit Hyperfokaler Distanz gemacht
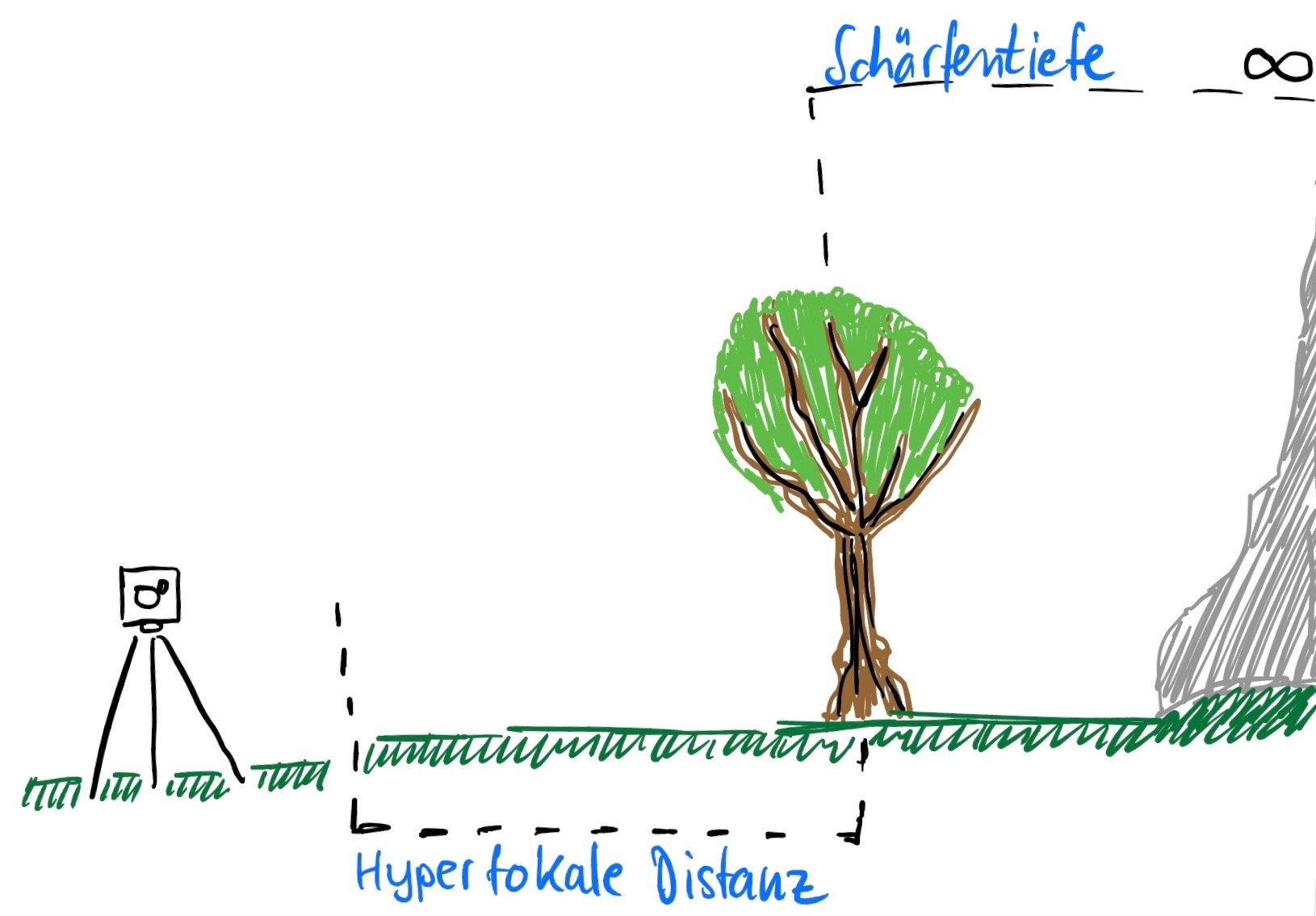
Anwendungsbeispiele
Wozu muss ich diese Theoretische Kacke jetzt Wissen fragst Du Dich zurecht. Vielleicht hast Du gerade ein bisschen mit Brennweite und Blendenzahl herumgespielt wie in unserem Teil 3 "die Blende" unseres #fotolern Projektes und Fokussierst auf ein Objekt vor den Alpen, des Mount Everest oder einfach Deinem Dorfberg. Jetzt hast Du das Objekt scharf aber den Berg nicht. Hm - Blöd, Du fokussierst Unendlich und Bämm Objekt unscharf. Was tun? Die Lösung: Hyperfokale Distanz! Denn für genau diesen Fall hat der Liebe Gott diese Hyperfokale Distanz erfunden.
Dazu habe ich noch 2 gute Grafiken im Internet gefunden die ich mal nachgezeichnet habe:
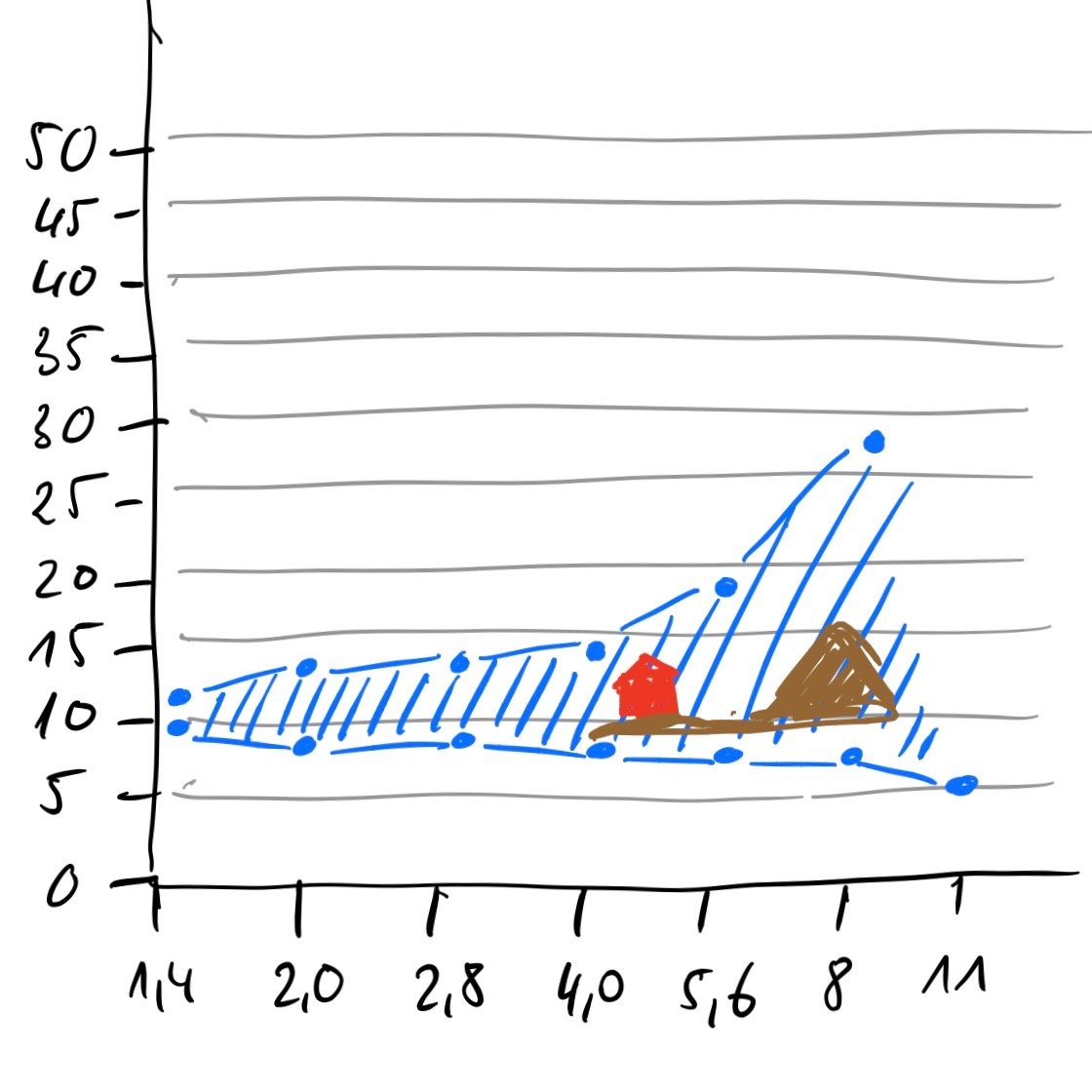
Das Objekt befindet sich in 10m Entfernung; der Schärfebereich ist gering
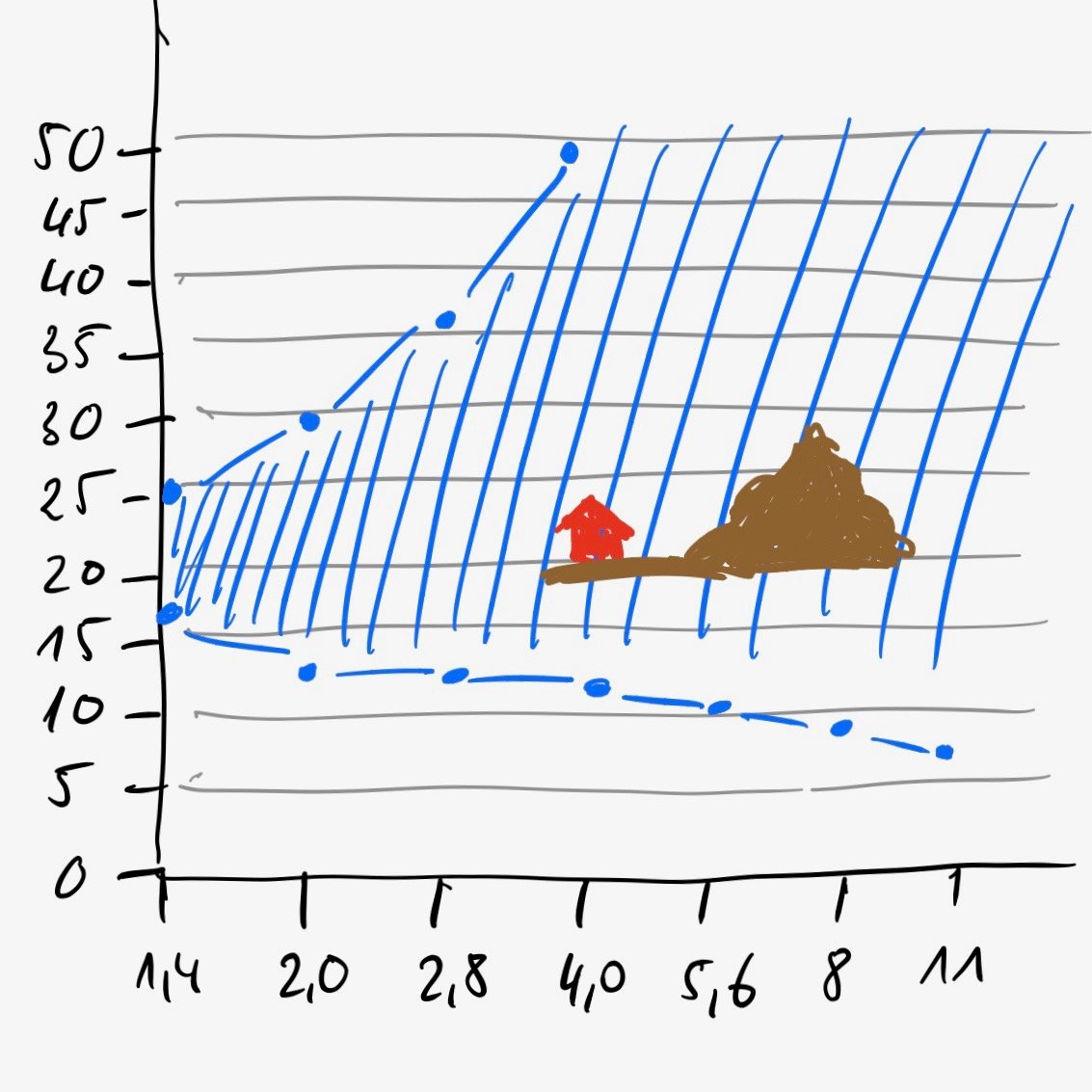
Das Objekt befindet sich in 20m Entfernung; der Schärfebereich ist wesentlich größer
die Hyperfokale Distanz ausrechnen
Gottseidank muss man die passende Distanz, bzw andere Parameter für das perfekte Bild nicht für alle Kameras händisch ausrechnen. Im Internet und App-Stores gibt es diverse Rechner.
- auf fotolehrgang.de gibt es einen Distanzrechner den man nur mit Brennweite und Blendenzahl füttern muss und schon spuckt er die Hyperfokale Distanz für verschiedene Coop Faktoren aus. Hier muss man nur Wissen welchen Crop - Faktor die Kamera hat.
- Photo-Buddy ist eine iOS App welche die passende Distanz und auch die richtige Blendenzahl für einen Abstand ausspuckt.
- Für Androiden gibt es z.B. HyperFocal Pro als App welche die gleichen Aufgaben erfüllt.
Es gibt eine Vielzahl mehr an Apps und Webseiten welche die gleichen Funktionen bieten. Einfach mal googlen oder im jeweiligen App Store suchen.
Zu guter Letzt
möchte ich Dir noch ein Video von Stefan Wiesner ans Herz legen. Stefan Wiesner erklärt es kurz und knapp ganz gut und verständlich.
Fazit
Eigentlich ist es gar nicht so schwer wenn man das ganze ein paar mal für seine bevorzugten Objektive ausgerechnet hat. Irgendwann stellt sich ein Gefühl dafür ein und man fokussiert passend aus dem Handgelenk. Der Tip von Stefan Wiesner am Ende des Videos mit den Zaunpfählen ist zum Üben ganz gut um ein Gefühl für die passende Entfernung zu bekommen. Einfach raus und ein bisschen herum probieren 😉

Das Projekt #Fotolern wurde von @altobee ins Leben gerufen und soll eine gemeinschaftliche Arbeit sein um Grundlagen und Wissen der Fotografie zu vermitteln. Der Fahrplan soll wie folgt ablaufen:
| Anfang | Ende | Thema |
|---|---|---|
| 12.3. | 25.3. | Ausrüstung |
| 26.3. | 8.4. | Motivwahl |
| 9.4. | 22.4. | Blende |
| 23.4. | 6.5. | Belichtung |
| 7.5. | 20.5. | Iso |
| 21.5. | 3.6. | Richtig belichten |
Bisherige Themen im Projekt:
