INTRODUZIONE
Ieri sono stato in giro per i quartieri periferici a Siena e passeggiando sono finito vicino ad un deposito idrico cittadino.
Così mi sono iniziato a chiedere come possa funzionare il sistema che riesce a portare l’acqua fino a casa mia.
Alla base di tutto c’è il principio dei vasi comunicanti, secondo il quale funzionano gli impianti idraulici privi di pompe nei centri abitati: l’acqua immagazzinata in cisterne situate nel punto più alto della città, riescono a far arrivare l’acqua ad ogni casa dalle condutture senza distinzione di piano.
CC0 Creative Commons, Fonte
Il principio dei vasi comunicanti è la legge fisica secondo la quale un liquido omogeneo versato in due o più recipienti uniti tra loro raggiunge il medesimo livello superficiale generando così un'unica superficie equipotenziale.
(Premessa: forze e pressioni sono dei vettori, ma nella dimostrazione che vi descriverò, verranno prese in considerazione solo come scalari, dato che si sviluppano interamente lungo la loro componente parallela all’asse verticale).
Ma quali leggi fisiche regolano il principio dei vasi comunicanti?
Prima di introdurre ogni concetto è importante definire la Legge di Stevino
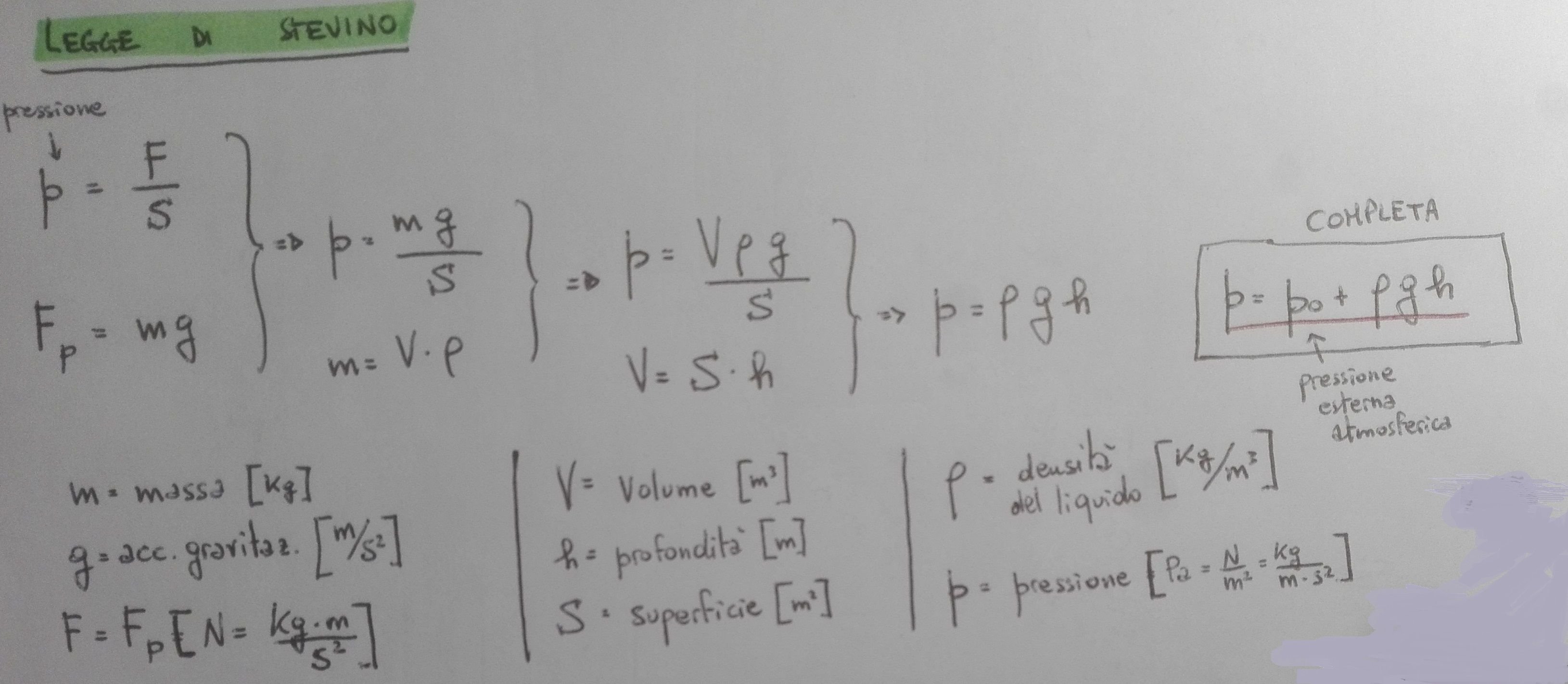
Tale legge spiega come la pressione nel liquido (p) vari a seconda di alcuni parametri:
- “p0” è la pressione atmosferica ed all’interno dell’esperimento si considera costante;
- “ρ” è la densità del liquido e nelle successive dimostrazioni considereremo sempre un liquido omogeneo; quindi è anch’essa una costante;
- “g” è l’accelerazione gravitazionale ed è una grandezza costante essendo la unica (circa) su tutta la Terra;
Di conseguenza intuiamo che p dipenda esclusivamente da “h”, che è l’unica variabile, e rappresenta la profondità alla quale la pressione viene misurata.
A questo punto iniziamo ad analizzare lo sviluppo del principio dei vasi comunicanti.
NOTA: tutti i contenitori sono aperti e su ognuno vi è sempre p0 come costante nel definire la pressione, quindi essendo un parametro comune non influisce e quindi non verrà proposto nella dimostrazione successiva.
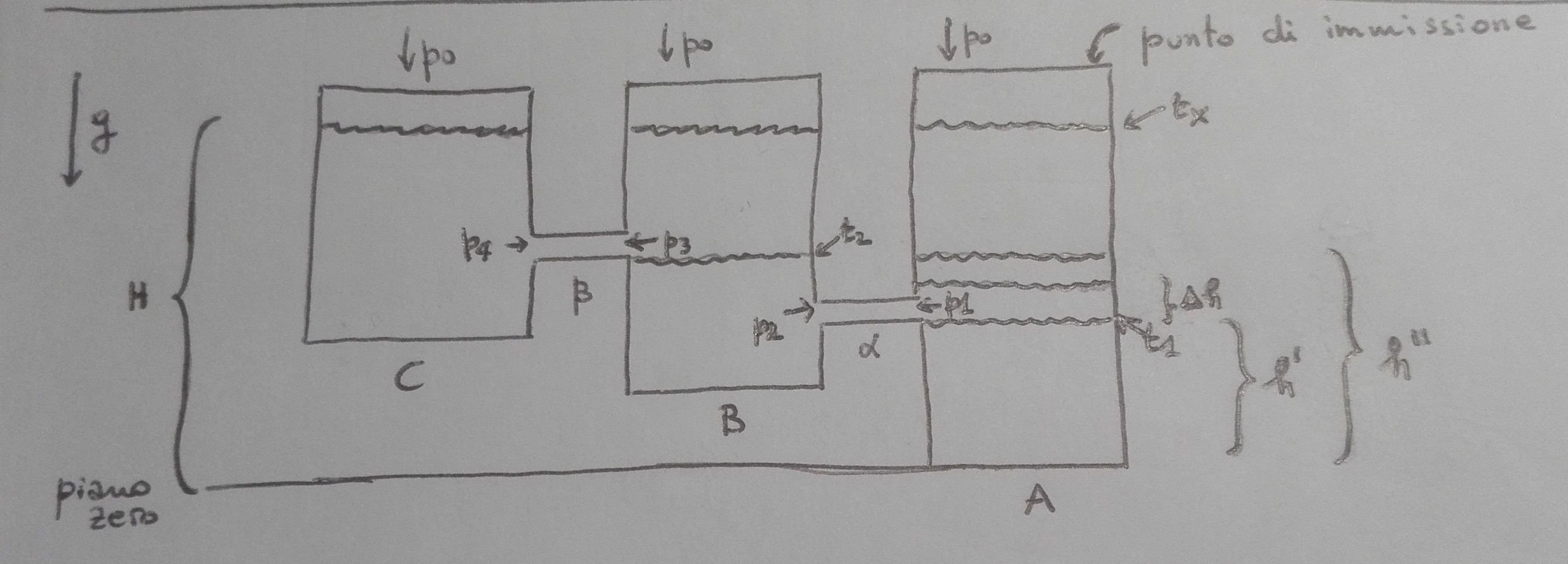
DIMOSTRAZIONE
Il liquido versato in A riempie il contenitore finché la superficie del liquido non raggiunge l’altezza h’ al tempo t1. In ogni istante successivo ogni aggiunta di liquido comporta ad un aumento di livello del liquido nel contenitore A (Δh) e sul foro α si genera una pressione p1 che vale p1= ρg Δh . Questa pressione non trova ostacolo nelle pareti come succedeva per valori minori o uguali ad h’ e trova quindi libero sfogo nella comunicazione α. Si noti che all’aumentare di Δh (ovvero la differenza tra l’altezza della superficie del liquido in A ed h’) corrisponderà una crescita proporzionale della pressione p1 e di conseguenza della velocità con la quale si riempie il vaso B.
Nei vasi comunicanti la pressione in uscita da un contenitore (p1) deve essere uguale a quella in entrata (p2) nell’altro. Finché questa uguaglianza non è verificata, il liquido continua a scorrere da A a B.
Perché p1 sia uguale a p2 è necessario che la colonna di acqua Δh sia uguale nei due vasi e quindi il livello superficiale sia lo stesso. Importante notare che quanto detto non coincide con il dire che il volume di liquido nel primo contenitore sia uguale a quello nel secondo: infatti se i due vasi poggiano su piani diversi questa situazione non si verifica, pur verificandosi il principio dei vasi comunicanti.
Giunti così al tempo t2, in cui il livello h’’ di A e B coincide, si verifica lo stesso fenomeno descritto sopra: aumentando di Δh, la pressione p3 differisce da zero e si libera nel vaso C che negli istanti successivi a t2 ha una p4=0 in prossimità del collegamento β.
Il riempimento di B (e quindi anche di A) riprende quando il liquido in C raggiunge anch’esso il livello h’’+ Δh.
Si noti che per ogni istante
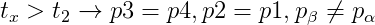.gif)
Questo perché la colonna di liquido che si trova sopra il livello del collegamento α è diversa e maggiore di quella che si trova sopra a β. Ciò significa che pβ<pα; la dimostrazione ce la fornisce la legge di Stevino descritta inizialmente (si consideri H il livello assoluto superficiale del liquido):
- pβ= ρg(H-h’)
- pα= ρg(H-h’’)
essendo h’<h’’ per definizione, si verifica che pβ<pα
Bibliografia
- "Elementi di Fisica - Meccanica/Termodinamica" (Mazzoldi-Nigro-Voci)
- Vasi comunicanti su YouMath
- Principio vasi comunicanti
Imagine CC0 Creative Commons, thanks to @mrazura for the logo ITASTEM. CLICK HERE AND VOTE FOR DAVINCI.WITNESS