Andando in montagna in una giornata di sole è possibile vedere cose molto lontane, tanto più lontane quanto più ci alziamo e tanto più si elevano sulla superficie terrestre gli oggetti che osserviamo. Poichè la Terra è sferica, esiste una distanza massima oltre la quale gli oggetti vengono nascosti dalla curvatura. Questa distanza è relativamente semplice da calcolare, e si può ottenere facendo semplici considerazioni geometriche: .gif)
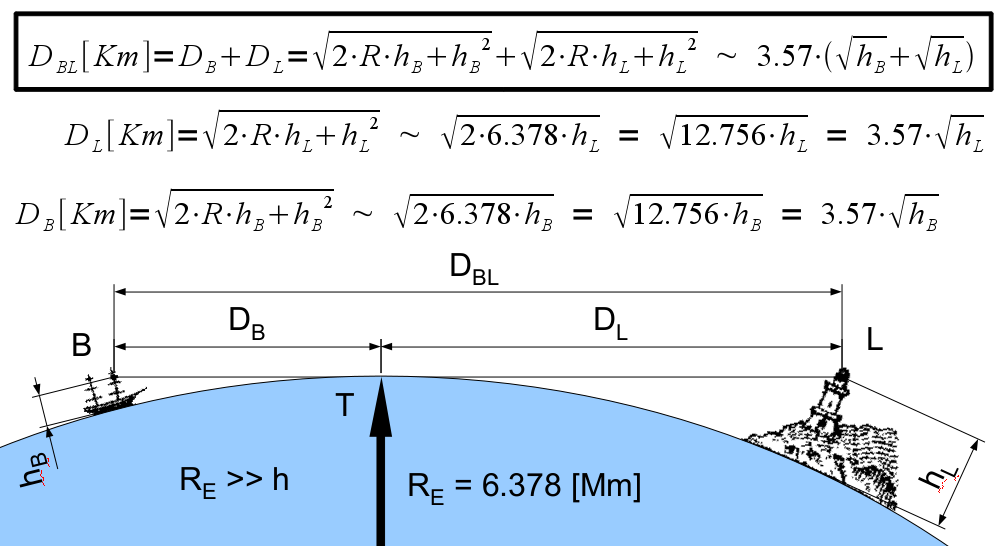
d è la distanza massima visibile, R è il raggio della Terra (circa 6300 Km) e h è l'altezza dell'osservatore sulla superficie.
Possiamo fare i conti con le altezze che più ci piacciono. Un osservatore in pianura ha un raggio visivo di circa 5 Km, rispetto ad oggetti "bidimensionali" spiattellati sulla superficie della Terra. Basta alzarsi di poco sulla superficie, e basta che gli oggetti osservati facciano lo stesso per vedere la distanza massima raggiungibile aumentare di molto, perchè bisogna sommare tra loro le rispettive distanze dell'orizzonte:
Imagine C00 Creative Commons
La distanza massima calcolata con la formula scritta sopra è quella teorica. Le condizioni metereologiche spesso non consentono una vista ottimale, ma c'è anche un problema molto più banale: la presenza di ostacoli tra l'osservatore e l'oggetto osservato. Grazie al sito https://www.heywhatsthat.com/ è possibile selezionare un punto qualsiasi della superficie terrestre, e scoprire quali punti sono visibili effettivamente, considerando gli ostacoli che ci sono di mezzo.
Facciamo una prova, mettiamoci sulla montagnola che ho a 10 minuti da casa.
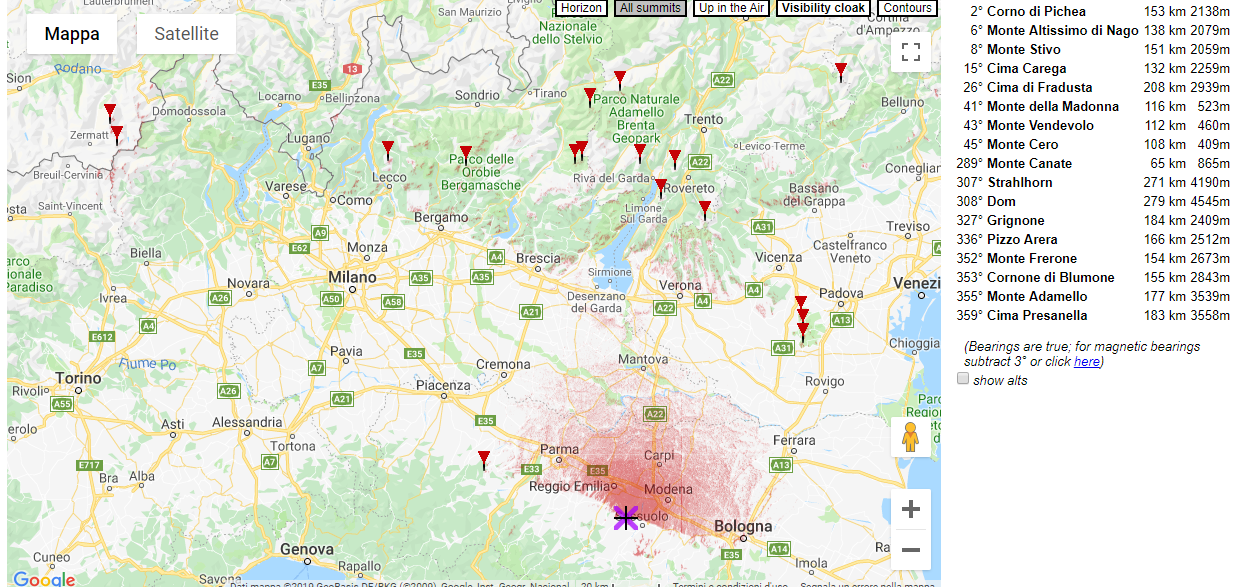
Il semicerchio rossastro e i picchetti rossi più lontani indicano rispettivamente i punti visibili nelle vicinanze e i picchi delle montagne visibili.
Notare come si possa (teoricamente) arrivare a vedere anche due montagne della Svizzera. Le prime Alpi sono perfettamente visibili.

Immagine dell'autore. Scattata dalla località indicata nella precedente immagine
Rivediamolo dal punto più alto della Sardegna.
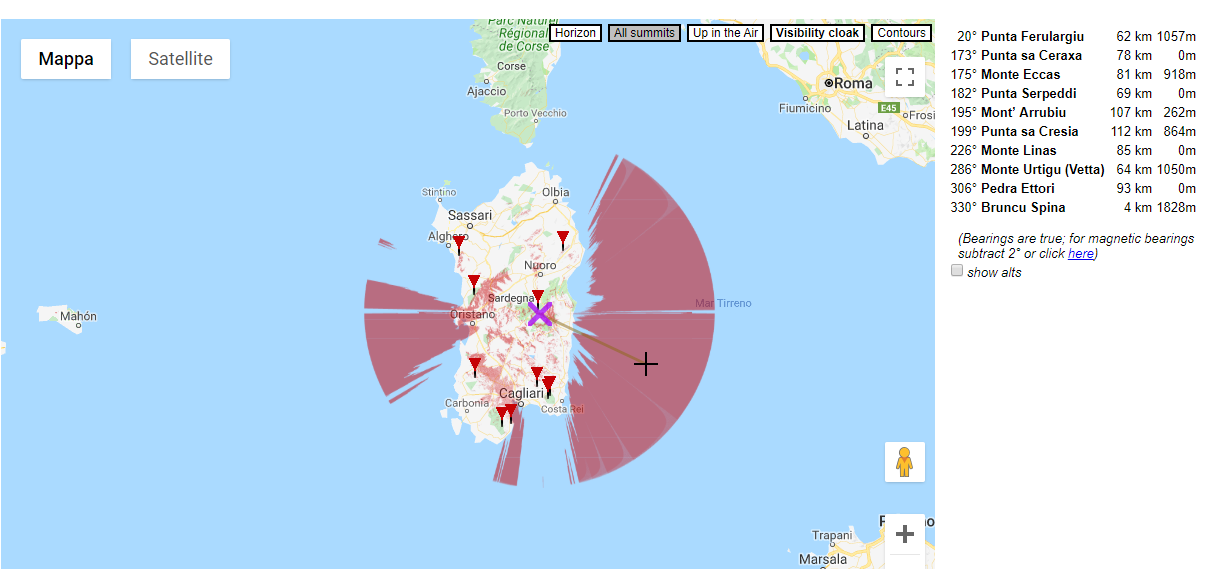
Giustamente il limite massimo di visibilità è descritto da una circonferenza, perchè viene prodotto da una superficie curva. Benissimo.
Se non ci fosse la curvatura potremmo vedere molto più lontano, teoricamente all'infinito (in assenza di atmosfera). Ma perchè c'è la curvatura?
Perchè la Terra non è piatta, e come lei gli altri pianeti?
Fondamentalmente perchè l'universo è pigro.
Principio di minimo
Piccola premessa: ogni oggetto posto a una certa distanza dal suolo possiede un'energia potenziale, che viene convertita in energia cinetica (movimento) quando l'oggetto è lasciato libero di cadere. L'energia potenziale dipende dalla massa del pianeta e dalla distanza da esso.
Un pianeta si forma per aggregazione, dovuta alla forza di gravità, di rocce. Nelle prime fasi della formazione, i pianeti non sono sferici, ma man mano che crescono le nuove rocce che si aggiungono sentono l'attrazione gravitazionale della massa di rocce già compattata, attrazione che cresce all'aumentare della massa stessa: aumenta la l'energia potenziale delle rocce: è qui che interviene il principio di minimo. In questo caso la tendenza è quella di minimizzare l'energia potenziale. Questo si verifica quando i pianeti raggiungono una certa dimensione. La forma geometrica che meglio soddisfa questa "necessità" è la sfera, e non è un caso: la sfera è la figura geometrica che a parità di volume minimizza la superficie esposta. Prendete un litro di acqua: se lo mettete in un cubo, la superficie esposta è maggiore rispetto a quella che trovereste su una sfera. Ecco dunque spiegato come mai i pianeti sono sferici, e i terrapiattisti sono...ditelo voi.

La cometa 67P/Churyumov-Gerasimenko non è sufficientemente massiva per diventare rotonda
Imagine C3.0 BY SA
I principi di minimo si ritrovano negli ambiti più disparati, e uno di essi è importante persino per spiegare come mai gli occhiali funzionano.
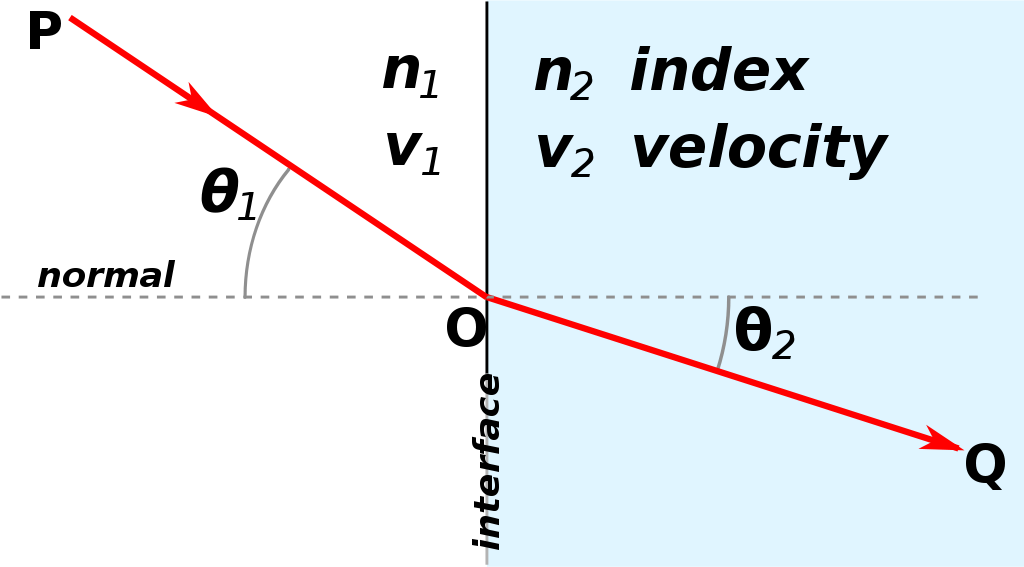
Gli occhiali, come tutte le lenti, deviano i raggi di luce che arrivano dall'esterno, e fanno si che questa arrivi correttamente al nostro occhio. La deviazione della luce avviene quando questa passa da un materiale all'altro, ad esempio aria-vetro, aria-acqua, ecc.. Pensate a un cucchiaio dentro a un bicchiere pieno d'acqua, o alle lenti di ingrandimento.
La deviazione della luce si può spiegare analizzando le proprietà microscopiche dei mezzi attraversati, oppure facendo di nuovo ricorso a un principio di minino. Poichè la luce cambia velocità a seconda del mezzo che attraversa, non è detto che la strada più rapida tra due punti sia una retta. In effetti, la strada che segue la luce è quella che minimizza il tempo impiegato per andare dal punto P a Q.
Creative Commons C00
Se così non fosse, la luce non devierebbe mai, e non riusciremmo e vedere nulla. Nulla di preoccupante, non avremmo gli occhi.
Questo fenomeno è strettamente collegato alle brachistocrone: sono le curve che minimizzano il tempo impiegato da un oggetto sottoposto alla sola forza peso, per scendere da un punto A a un punto B.
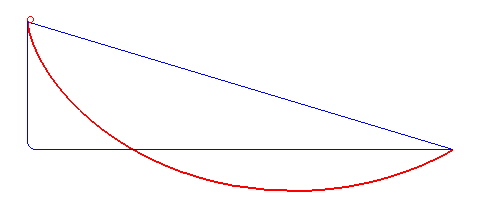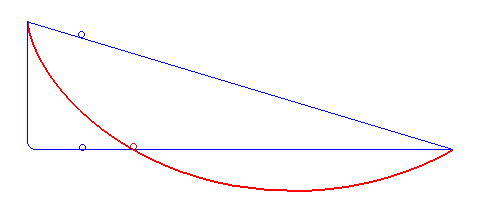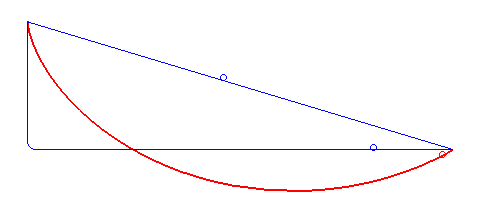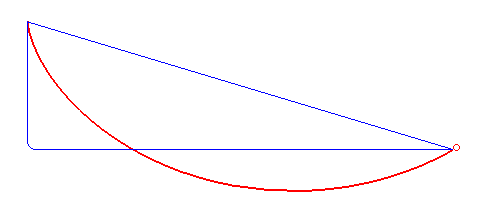
La brachistocrona in rosso
Creative Commons C00
Questo approccio è molto utile per la risoluzione di problemi fisici anche complicati, come ad esempio la determinazione teorica delle energie di ionizzazione degli atomi, oppure in economia.
Non è l'unico caso in cui dei principi propri della fisica vengono utilizzati anche al di fuori, ad esempio alcune equazioni che descrivono la distribuzione del calore nello spazio possono essere di nuovo applicate in ambito economico. Oppure le leggi che descrivono i gas in termini statistici, possono essere applicate al volo degli uccelli.
Certamente si tratta di fenomeni molto diversi tra di loro, ma possono essere ricondotti e descritti dalle medesime equazioni, ovviamente riviste opportunamente.
Questo per ribadire quanto la ricerca sia fondamentale, e quanto spesso si riveli utile in campi del tutto inaspettati.
Abbiamo dunque visto che l'universo sembra rispondere ai principi di minimo. È davvero così o è una nostra percezione dovuta al modo in cui lo descriviamo? Se usassimo un linguaggio diverso dalla matematica, ci accorgeremmo comunque di questo principio? Qua entriamo chiaramente in ambito filosofico, e diverse opinioni sono legittime. Intanto i principi di minimo continuano a funzionare benissimo.
Fonti
- http://www.damtp.cam.ac.uk/user/db275/LeastAction.pdf
- https://www.cmi.ac.in/~debangshu/fermat.pdf
- https://www.ast.cam.ac.uk/~wyatt/lecture4_planetformation.pdf
- https://sites.math.washington.edu/~conroy/m120-general/horizon.pdf
- https://www.heywhatsthat.com/

Immagine CC0 Creative Commons, si ringrazia @mrazura per il logo ITASTEM.
CLICK HERE AND VOTE FOR DAVINCI.WITNESS
