Sarà che lo vedi girare, sarà che ne so, ma trovo il disco in vinile (e il giradischi) un bellissimo oggetto d'arredamento. E i crepitii che ogni tanto emette, che sono tecnicamente dei disturbi, finiscono per dare un tocco in più alle canzoni.
Mi ricordo una volta a casa di un mio amico, messe sul giradischi un vinile. “Tra la Via Emilia e il West”, storico disco dal vivo di Guccini. Aiutato da un signor impianto di amplificazione, un gran bel suono.
Che poi si sente nettamente meglio, no? Si? No? Rispetto ai CD, o alle chiavette dico. Se avete l'orecchio molto allenato potreste sentire lievi differenze. Dipende poi anche dal tipo di computer che registra il suono.
Si perchè nella conversione da analogico a digitale viene persa irrimediabilmente un po' di informazione. Questo perchè un computer codifica le informazioni sotto forma di “bit”, numeri, cioè entità discrete. Il bit (0,1) è la parte più piccola, indivisibile, di informazione. Ciò porta inevitabilmente a una perdita della stessa.

Imagine C00 Creative Commons
Un segnale acustico, ad esempio il suono di una corda di chitarra pizzicata, è continuo nel tempo, ossia non si interrompe mai finchè la corda vibra: in qualunque istante posso misurare l'intensità del suono e sono certo che troverò un valore diverso da zero. Un registratore analogico usa una serie di strumenti meccanici che permettono a una punta di incidere un disco. Questo succede in modo continuo, perchè i sistemi meccanici sono messi in vibrazione dalle onde sonore.
Quando un computer memorizza un suono sotto forma di bit, questa proprietà viene meno, perchè per sua natura un computer memorizza informazioni discretizzandole, con i bit appunto.
Il suono analogico dello strumento viene campionato a intervalli regolari. A punto del campionamento viene assegnata una sequenza di bit che contiene informazioni relative al suo collocamento temporale.
Se volessimo un segnale perfettamente riprodotto dovremmo campionare tutti i punti del segnale analogico, ma poiché è continuo i suddetti punti sono infiniti. Dunque servirebbe una memoria infinita per memorizzare tutto il segnale. Quello che si può fare è rendere il campionamento sufficientemente fitto, per riprodurre il segnale con una precisione sufficiente ad evitare l'alaising, cioè l'errata trascrizione del segnale.


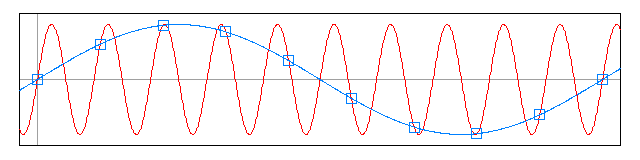
Se il numero di punti campionato è troppo basso, il segnale originale (rosso), può essere interpretato come un altro segnale completamente diverso (blu)
Immagini C00 Creative Commons 123
Viene in aiuto del computer anche il teorema del campionamento di Shannon. Esso afferma che se la frequenza di campionamento è almeno il doppio della frequenza del segnale, è possibile ricostruire il segnale analogico senza errori. Ad esempio, l'orecchio umano è in grado di sentire suoni compresi tra i 20 Hz e i 20000 Hz. Dunque basterà campionare il suono con una frequenza di 40000 Hz per assicurarci di poter riprodurre esattamente il suono prodotto dagli strumenti musicali.
Siamo a posto quindi? No, il teorema di Shannon garantisce solamente che sotto determinate condizioni si può registrare il segnale in modo inequivocabile. Perchè se anche potremmo (in teoria) riprodurre il segnale analogico con certezza, dovremmo comunque avere a disposizione una memoria infinita. Infatti, se ho N bit a disposizione, posso descrivere solo un numero finito di ampiezze. Allora viene fatta ancora una volta una discretizzazione, in questo caso dell'ampiezza.
Si divide il campo di misura in un numero finito di intervalli contigui. Si trova il valore centrale di ogni intervallo. Ogni punto che cade nell'intervallo viene trasformato ricondotto al punto medio.
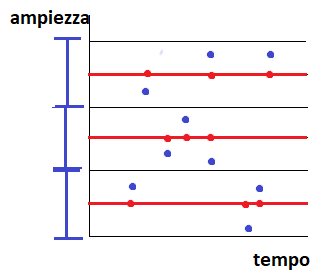
I punti blu rappresentano il valore reale del segnale, la linea rossa i punti medi dell'intervallo
Immagine dell'autore
Facendo questo si commette un errore, perchè si alterano i valori reali. Ma è un errore tanto grosso?
Dipende dal numero di bit che vengono utilizzati. Con N bit è possibile avere 2^N intervalli.
Dunque con 10 bit ho 4096 livelli di discretizzazione. Sono sufficienti? Dipende dal segnale, e dalla risoluzione che cerchiamo. Più è alto il numero di intervalli minore è l'errore commesso, perchè è più fine la suddivisione delle ampiezze. Chiaramente per le applicazioni pratiche viene utilizzato un margine d'errore tale da rendere indistinguibile o quasi, all'orecchio umano, la differenza tra segnale analogico.
Può essere che tra vinile e digitale ci sia davvero una differenza, ma è minuscola. C'è chi la sente (o dice si sentirla!) e chi no. Comunque Spotify non è male.
Certamente c'è un fattore soggettivo. L'orecchio umano traduce le vibrazioni dell'aria in segnali elettrici, ma questo meccanismo non è perfetto. Un suono potente nasconde un suono debole ravvicinato nel tempo. Più suoni della stessa ampiezza ma di diversa frequenza sono percepiti come suoni più deboli, con una frequenza “spalmata” tra le frequenze dei suoni originari.

Immagine CC BY-SA 4.0
Naturalmente la sfida tra analogico e digitale sarà vinta da quest'ultimo: con l'aumento della capacità di memoria, lo streaming, la disponibilità sempre maggiore di banda: ogni differenza sarà piallata. Con la differenza che il digitale non incappa in tutti gli svantaggi di un segnale analogico, che possono andare dal deterioramento del supporto fisico alle avverse condizioni ambientali.
La manipolazione del segnale possibile in digitale è anni luce più avanzata di quella possibile un tempo. Oltre alla compressione dei file, il digitale ha permesso una diffusione senza precedenti della musica.
Nel 2017 i ricavi derivanti da servizi di streaming a pagamento come Spotify hanno superato per la prima volta i ricavi derivanti da vendite fisiche o download. Frega poco della perdita di informazioni. I supporti digitali sono trasportabili ovunque, comodamente. Ma il vinile continuerà a darmi l'idea della musica ascoltata "con calma", gustata come si deve.
Fonti:
- C.E. Shannon: A mathematical theory of communication (1948): https://pure.mpg.de/rest/items/item_2383164/component/file_2383163/content
- M. B. Patil: ADC and DAC circuits: https://www.ee.iitb.ac.in/~sequel/ee101/ee101_dac_1.pdf
- https://www.embedded.com/design/configurable-systems/4025078/Understanding-analog-to-digital-converter-specifications
- http://www.dii.unimore.it/~lbiagiotti/MaterialeCA1415/CA-B-07-ImplementazioneRegolatori.pdf
- https://www.wired.it/economia/business/2018/04/26/streaming-musica-mercato/
Mi trovi su
Twitter
Enlte
ref.code: 390df60d7c0630f51f4ade991680faa6
Letture consigliate (link di affiliazione Amazon):
Barabasi, Albert-Laszlo Linked: The new Science of Networks
Marco Potenza - Dio non gioca a dadi
David J. Hand - Il caso non esiste
Stephen Hawking - Dal Big Bang ai buchi neri
Carlo Rovelli - Sette brevi lezioni di fisica
Bertold Brecht - Vita di Galileo
Paolo Nespoli - Dall'alto i problemi sembrano più piccoli

Immagine CC0 Creative Commons, si ringrazia @mrazura per il logo ITASTEM.
CLICK HERE AND VOTE FOR DAVINCI.WITNESS
