안녕하세요. Jay라고 합니다. 처음으로 steemit에 글을 올려보네요. 두근두근.
가상화폐에 빠져서 비트코인과 블록체인이 어떻게 기술적으로 동작하는지 알아보고 있습니다.
블록의 해더에 있는 머클루트 필드를 보고 "이게 뭐지?"라는 궁금증을 시작으로 머클루트가 왜 있는가 조사를 해보았습니다. 구어체가 아니라 딱딱하게 느껴질수도 있지만, 머클루트가 뭔지 궁금한 분에게 조금이라도 실마리를 제공했으면 좋겠습니다.
머클트리(Merkle Tree)
머클트리(Merkle Tree) 혹은 해쉬트리(Hash Tree)라고 데이터구조는 Ralph Merkle이라는 사람이 1979년에 특허를 낸 개념이다. 1979년에 고안한 개념이 비트코인 블록체인에 유용하게 사용되고 있는게 흥미롭다. 참고로 2002년에 이 특허는 만료되었다고 한다.
머클트리를 이용하여
- 트랜잭션들의 정보들이 변경되었는지 확인할 수 있고,
- 머클루트만 해더에 담아서 트랜잭션들의 유효성을 보장할 수 있고,
- 머클 경로(Merkle Path)를 제공하면 특정한 트랙잭션이 블록에 유효하게 있는지 효율적으로 검사할 수 있다.
1. 트랜잭션들의 정보들이 변경되었는지 확인할 수 있다.
트랜잭션이 1, 2, 3, 4 총 네 개가 있다고 하면 img-1처럼 머클트리를 그릴 수 있다. (여기서는 이해를 돕기 위해서 해쉬를 적용하지 않고 단순히 숫자문자를 연결하는 것으로 설명한다.) 첫번째 1과 두번째 2를 합쳐서 바로 위에 12라는 부모 노드가 생긴다. 3, 4도 마찬가지로 34라는 부모노드 생긴다. 12노드와 34노드위에 다시 부모노드 1234가 생긴다.
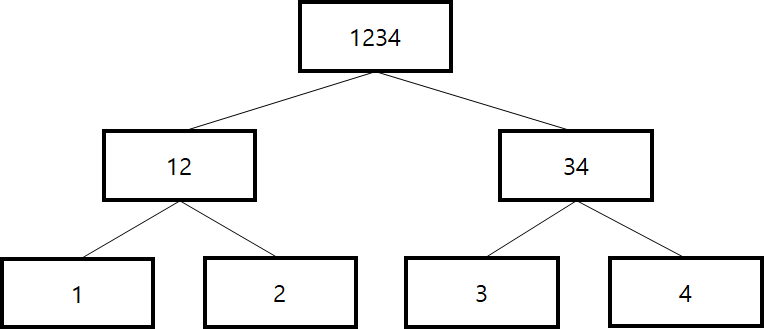
img-1 : 머클트리 예시
원래 트랙잭션이 1, 2, 3, 4 총 네 개가 있어야 되는데, 누군가 2를 5로 바꿨다고 해보자. 우리는 이미 머클트리를 그려봤고 제일 부모노드에 있는 값(머클 루트 값)이 1234라는 것을 알고 있다. img-2처럼 변경된 5값으로 다시 머클트리를 계산해보면 머클루트 값이 1534가 된다. 우리가 알고 있는 원래 1234값과 다르기 때문에 변경되었다는 것을 알 수 있다.
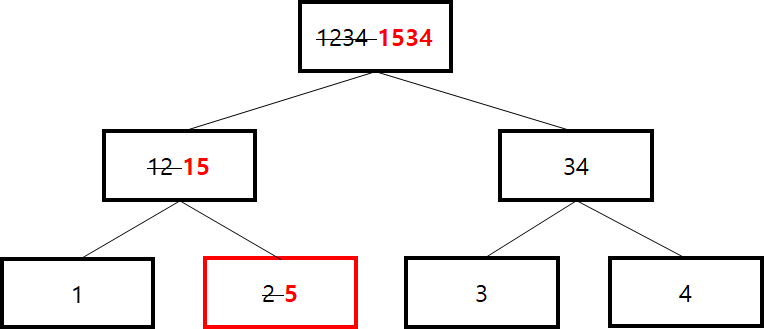
img-2 : 변경된 자료 발생
실제로는 1, 2, 3, 4는 트랙잭션이 가지고 있는 고유ID(해시값) 값이 되고, 트랙잭션 ID를 더하고 그것을 해쉬한 값이 부모 노드의 값이 된다.
2. 머클루트만 해더에 담아서 트랜잭션들의 유효성을 보장할 수 있다.
마이닝을 할 때 블록의 해더값을 해시로 만든다. 트랜잭션들을 담고 있는 블록의 바디가 직접적으로 해시되지 않는다. 그럼 간접적으로 트랜잭션 정보들이 해시된다? 블록의 해더에 머클루트 값이 있기 때문에 간접적으로 해시 되는 것이다. 위에서 머클루트 값이 다른 것을 보고 변경된 트랙잭션 정보가 있다는 것을 알 수 있었다. 블록의 해더에 수정할 수 없도록 머클루트 값이 보관되어 있기 때문에, 트랙잭션들을 직접적으로 해시할 필요가 없는 것이다. 블록 바디에 있는 트랙잭션 값들도 다 포함해서 해시할 필요 없이 머클루트만 담아서 해시해도 트랙잭션들의 유효성을 보장할 수 있다. 블록에 담겨있는 트랙잭션 값들의 머클루트 값을 계산해서 블록의 해더에 있는 머클루트 값과 같은지 확인할 수 있기 때문이다.
3. 머클 경로(Merkle Path)를 제공하면 특정한 트랙잭션이 블록에 유효하게 있는지 효율적으로 검사할 수 있다.
img-1에서 거래 1,2,3,4 네 가지가 있을 경우의 해시트리를 그려보았다. 우리는 머클 루트 값이 1234라는 것을 알고 있다. 블록에 거래 4가 유효하게 존재하는지 확인하고 싶다면 어떻게 할까? 머클 경로(Merkle Path)를 제공하면 효율적으로 검사할 수있다.
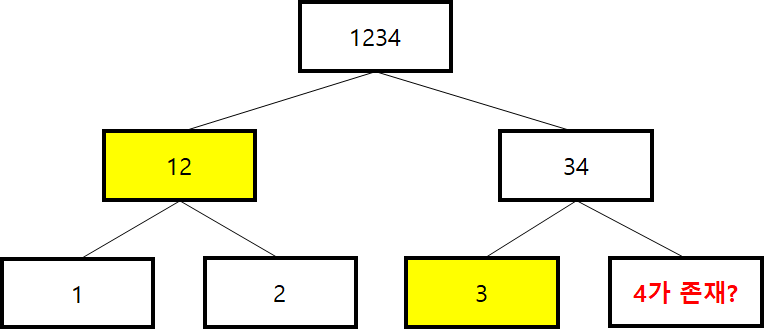
*img-3 : 머클 경로
머클 경로로 3 12 값을 주면, 3과 4을 합쳐서 34 그리고 12와 34를 합쳐서 1234 값을 얻을 수 있다. 우리가 알고 있는 머클루트값 1234와 동일하다는 것을 확인할 수 있고, 블록에 거래 4가 있다는 것을 증명할 수 있다. 전체 트랜잭션을 다운받아서 검사하는 대신에 이렇게 머클경로와 블록의 해더 값만 다운받아서 검사할 수 있게 된다.
기타 : 머클 트리는 바이너리 트리 구조로 되어 있다.
바이너리 트리 구조로 되어 있다는게 무엇일까? binary 두 개로 이루어진 것을 뜻한다. 그림 예제들을 보면 부모 노드 하나에 자식 노드 두개가 연결되어 있는 것을 볼 수 있다.
특정한 트랜잭션이 유효한지 볼려면 제일 아래부터 값을 더해서 올라간 다음 제일 위의 머클 루트 값과 같은지 확인을 하였다. 예시에서는 그냥 값을 더했지만 실제로는 해시를 생성한다. 이제 바이너리 구조의 장점이 나온다.
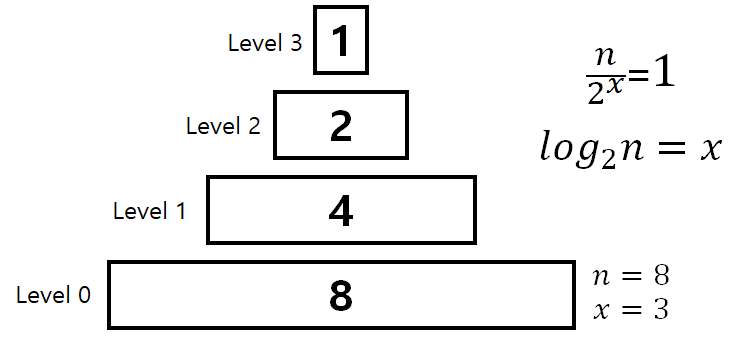
img-4 : 바니어리 트리 구조 설명
트랜잭션 갯수 n이 많이 늘어나도 상대적으로 해시 작업을 수행해야 하는 횟수 x는 천천히 늘어나게 된다. 트랙잭션 갯수가 10000개여도 해시작업을 수행해야 하는 횟수는 log2 10000 = 13.29, 즉 14번만 수행하면 된다.
제가 공부한 내용을 바탕으로 작성하였습니다. 혹시 잘 못 설명된 내용이 있으면 댓글로 알려주세요.
