By imagining various kinds of reflected worlds, we can understand some of the basic symmetries of physics.
- Parity symmetry (P-symmetry) exchanges left and right;
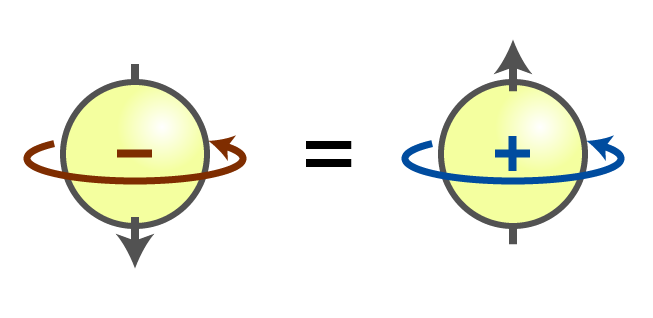
- Charge conjugation (C-symmetry) exchanges matter and antimatter (positive and negative);
- Time reversal (T-symmetry) exchanges future and past.
Surprisingly, the combination of all 3 mirrors parity, charge, and time does appear to be an exact symmetry of the laws of nature.
Let's examine these 3 fundamental symmetries, or mirrors, of our universe reflections in space, matter, and time.
Is it possible to tell the world in the mirror from our own? If it is impossible, then the mirror represents a basic symmetry of nature. If it is possible, then nature is not symmetric in that way, and the change matters to the laws of nature. This touches on some of the most unexpected discoveries in the history of physics and includes a clue to a basic puzzle about the cosmos—namely, how atoms could exist.
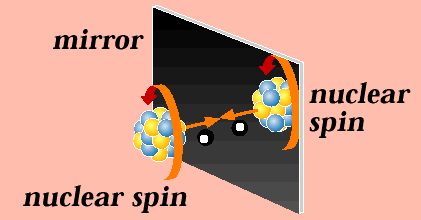
Our first mirror reflects space, exchanging left and right. Physicists call this parity.
Our universe was long assumed to possess parity. Newton’s laws of motion and the laws of electromagnetism work exactly the same way in the reflected world. In 1956, Chen Ning Yang and Tsung-Dao Lee realized that the nuclear forces, the force responsible for beta decay, make a fundamental distinction between left and right. Their theory was later confirmed by Chien-Shiung Wu. Beta decay almost always emits particles in one direction (i.e., asymmetrically), following a right-hand rule.
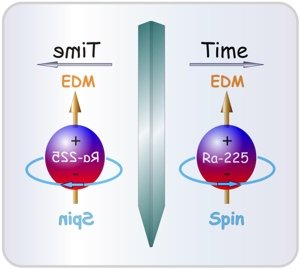
The next mirror is not a reflection in space but in the properties of matter, called charge conjugation. This mirror turns matter into antimatter, and vice versa.

Antimatter was predicted in 1927 by English physicist Paul Dirac, who was trying to reconcile relativity and quantum theory. Antimatter is made of antiparticles—particles of the same mass but opposite electric charge to the particles in the matter we know. Dirac’s prediction was confirmed when positrons, of the same mass but opposite charge as electrons, were discovered in 1932 by Carl Anderson. Why matter is so common and antimatter is so rare is actually a profound mystery. What would an antimatter universe look like? It would look pretty much the same as our universe. Positrons would repel positrons just like electrons repel electrons, and so forth. However, charge conjugation is not an exact symmetry. As with parity, the direction of beta decay is flipped. However, if you combine parity and charge conjugation—in other words, flip the universe twice, beta decay looks symmetrical again! One asymmetry that remains in this double-flipped universe has to do with rare particles called K-mesons. The combination of these laws is almost, but not quite, a symmetry.
The third and final mirror is time-transformation exchanging future and past.
It does not seem possible that this is a symmetry, thanks to the second law of thermodynamics, the arrow of time. However, the second law is always about huge numbers of particles, and it is only a statistical law. Entropy decreasing is not strictly impossible, only incredibly unlikely. When 2 similarly charged particles approach each other, at a certain point they repel and fly apart. Run the process backward, and it looks exactly the same. No one is quite sure how to solve this paradox: The universe seems to have time-symmetric laws, but its large-scale behavior is not at all the same in the time mirror.
Together, relativity and quantum theory imply that the combination of all 3 mirrors must be an exact symmetry of nature.
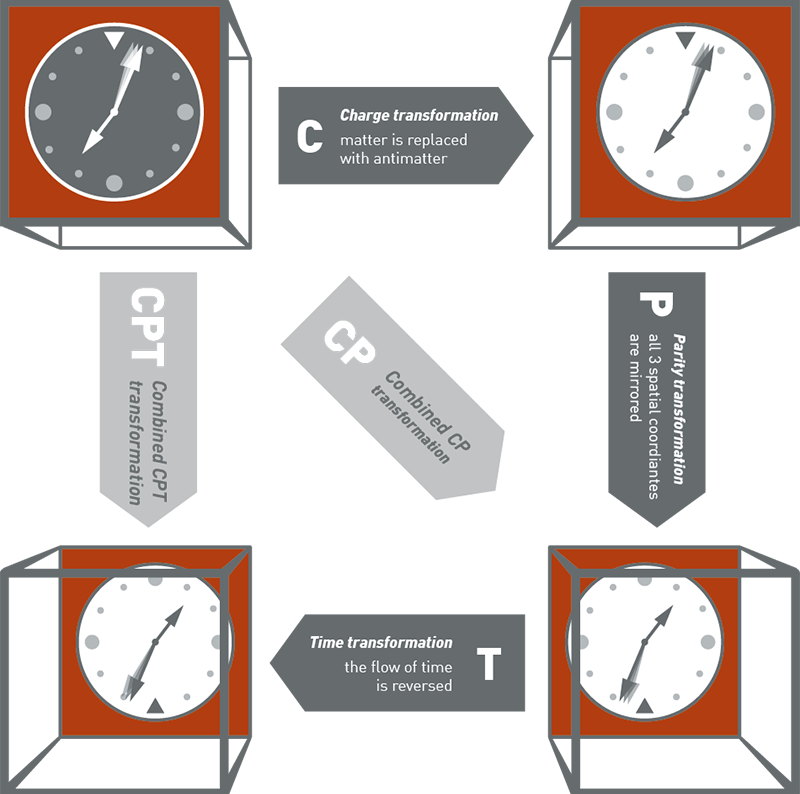
Charge, Parity, and Time Reversal (CPT) Symmetry
Symmetry in Sci-fi

The spaceship in the science fiction movie Doppelgänger visits a version of Earth that was reflected in the parity-mirror.
