Il Paradosso del compleanno un apparente paradosso di teoria della probabilità. Ho detto apparente, infatti non c'è assolutamente nulla di paradossale, la matematica in questione è ben nota, semplicemente la risposta al quesito che vi proporrò fra poco è molto diversa da quanto ci si aspetta intuitivamente. Il paradosso è stato definito in modo chiaro nel 1939.
Dunque, il quesito di cui vi parlavo è il seguente: "Qual è il numero di persone necessario affinchè la probabilità che due persone compiano gli anni lo stesso giorno sia superiore al 50%?" Immaginiamo dunque di voler mettere in una stanza N persone, in modo tale che la probabilità che due di esse compiano gli anni lo stesso giorno dell'anno sia superiore al 50 %.
Come possiamo calcolare N?
Per facilitare i calcoli, possiamo immaginare di calcolare la probabilità inversa, ovvero la probabilità che una persona non compia gli anni lo stesso giorno di un altra. Supponiamo inoltre che gli anni abbiano tutti 365 giorni (l'anno bisestile non cambia praticamente il risultato del calcolo)
Supponiamo che inizialmente ci siano solo due persone (A e B) nella stanza: la probabilità che una non sia nata lo stesso giorno dell'altra è di
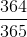
Adesso aggiungiamo una persona (C): la probabilità che C non sia nata lo stesso giorno di A e B è data da:
.gif)
infatti, le due probabilità vanno moltiplicate tra loro, perchè i due eventi sono indipendenti
Ricordiamoci però che questa è la probabilità che le persone non compiano gli anni lo stesso giorno, mentre a noi interessa l'evento contrario.
Prima di proseguire un chiarimento di carattere matematico
La probabilità varia da 0 a 1, dove 0 è..0% e 1 è 100%, 0,5 è 50% e così via...
Ovviamente la somma di probabilità di due eventi contrari è sempre 1. Pensateci, la probabilità che N persone compiano gli anni lo stesso giorno sommata alla probabilità che N persone non compiano gli anni lo stesso giorno è 1. Per forza, non può essere altrimenti! O compiono gli anni lo stesso giorno oppure no, eh!
Torniamo al nostro problema, adesso ripetiamo il procedimento, avrete capito come funziona.
.gif)
Andiamo avanti fino a che la probabilità che due persone non compiano gli anni lo stesso giorno sia inferiore al 50%, in questo modo la probabilità che invece accada il contrario è maggiore del 50%
Calcoliamo quindi l'evento contrario:
.gif)
Dove "!" indica il fattoriale del numero. Se abbiamo un numero Z>0 allora il fattoriale di Z è dato dalla moltiplicazione tra loro di Z e di tutti i numeri inferiori ad esso (escluso lo zero), ad esempio:
.gif)
Bene, a conti fatti, il nostro N affinchè P(N)>0,5 è...23! Se 23 persone sono nella stessa stanza, allora la probabilità che due persone compiano gli anni lo stesso giorno è maggiore del 50%. 23 è un numero basso, controintuitivo, paradossale. Le stime che a primo impatto avremmo potuto fare sono molto più alte. Guardate inoltre dal grafico quanto aumenta la probabilità in funzione di N.
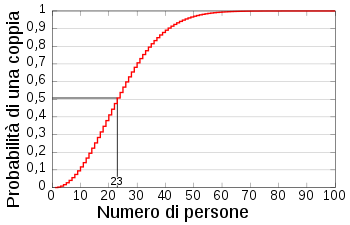
(da wikipedia)
La probabilità sale molto rapidamente nel range tra le 10 e le 40 persone, numero a cui siamo quasi sicuri di avere una coppia. Bello eh?
