My Math: Collatz Conjecture (Part 1 - An Introduction)

Most people I talk to don't realize that there are still hundreds of math problems which are easy to understand but still remain unsolved. One such problem is Collatz Conjecture. I recently read a post (@sheagar/an-artist-with-writer-s-block) about how planning can get in the way of doing. It was a guy who had planned for years to create his own comic but he never really got started because he never just made himself begin.

That hit home with me as I've had quite a few projects over the past few years that I can't seem to get off the ground. I absolutely love working on unsolved math problems! Please take a 30 second pause to laugh at me, then continue reading if you like lol.

image from www.jasondavies.com

Collatz Conjecture states that if you start with any positive whole number and play by a couple of rules, you'll always find your way back to the number 1. The problem is, it's never been proved.

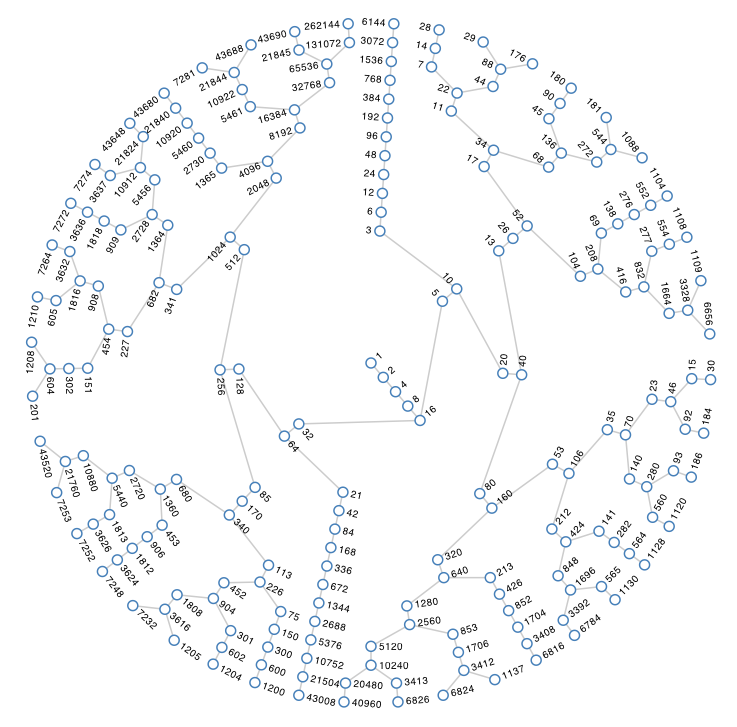
Rule 1: If you have an odd number, you must multiply it by 3 and then add 1.
Rule 2: If you have an even number, you must divide by 2 as many times as you can until it becomes an odd number again.

Example: Let's start with the number 3:
3 is odd, so multiply by 3, then add 1 to get 10.
10 is even, so divide by 2 to get the odd number 5.
5 is odd, so multiply by 3, then add 1 to get 16.
16 is even, so divide by 2 to get 8
8 is even, so divide by 2 again to get 4.
4 is even, so divide by 2 again to get 2.
2 is even, so divide by 2 again to get 1.
1 is odd, so multiply by 3, then add 1 to get 4.

Now you can see that the sequence is stuck in a so called trivial cycle: 4,2,1...

Notice how easy the problem is to grasp? Most 8 year olds could understand the rules and play around with it.

Above is a picture of a few of my pages of scribble. I'd say that's at least 10 hours of messy handwriting there.

As you can see, I started working on a paper I'd hope to one day publish back in December 2016. I've never been to college so it's a bit of a struggle. Everything I've done is either through experimentation (playing with numbers) or ideas I've had of building on the progress of others. I typically prefer working on my own, as playing with the numbers my way is what I truly love. If I run with someone else's idea, it won't hold as much meaning.

I've studied various methods of attack. There is the graphical method, which creates pretty fractals like this one but won't lead to a solution:

There is the method of converting numbers to binary, and I spent some effort on this only to find that my intuition says there's nothing useful there.

My method is to consider that there is a solution with a non-trivial cycle and to not worry about the runaway case for now. Imagine a starting number that is much higher than our computers have tested. Maybe, when put through the iterations, eventually it returns to the starting number. As of 2009, the conjecture has been checked by computer for all starting values up to 5×2^60. In other words, there's no point testing numbers yourself as everything you could write down or easily test on your computer has already be verified to return to 1.

I think I've made some progress, but as I'm not friends with any college math professors, it's hard for me to know. I've come up with a method of finding limits on the problem, but I haven't yet surpassed what's already been discovered. However, if my approach is unique, it could provide valuable information on the conjecture.

As I work on Collatz Conjecture, I'll post my work on Steemit. As of now, Steemit doesn't have a good way of expressing equations. Right now I'm using LaTeX software which allows pretty simple creation of equations and outputs as a PDF. Why use Steemit? Everything is time stamped here and I know that can't be tampered with since it's part of the Steem block chain. That's quite valuable to me as an amateur mathematician. Also, it's something I like sharing because the topic holds value to me.