Today I am goint to talk about ADS geometry. which is called anti-de sitter space .
First of all, there is de sitter space which named after astronomer Willem_de_Sitter. Mathematically, anti-de-sitter space is a "maximally symmetric space of Lorentzian manifold with negative scalar curvature". Let's talk this in more detail. The terminology maximally symmetric means it has maximum number of killing vector, and Lorentizan means introducing time variable with different sign, and negative scalar curvature means, its Ricci scalar is negative.
Physically, it means among the solution of Einstein's field equation, it has negative cosmological constant. (For this cosmological constant term let's call it shortly c.c. If c.c=0, this maximally symmetric space represent Minkowski space, and for positive c.c, it denotes de-sitter space. )
Let me introduce some famous picture which often mention when we came up Ads space.
[Mauritz Cornelius Escher, Circle Limit IV]
Which figure did you see? Devil or angel?
Since ads geometry has negative curvature, the figures in the middle seems big but as going for the boudnary the figures become smaller.
Now think of some computation, in this post i want to check its definition starting from its ads metric.
First in D-dimensional ads spacetime in poincare patch[maybe latter I will post about this in more detail, this is kinds of representation of coordinate], the shape of metric is given as follows
here the index 
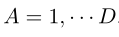A,B denotes space time and \eta_{\mu\nu} means flat D-1 Minkowski metric. Write this in a traditional way [as in the context of general relativity] we can write
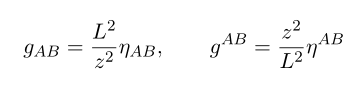
with this we can compute its connection and Riemann tensor. Before that we have to know the shape of differentiation of metric. Since except z-direction, this metric is essentially flat, thus
with this we can compute connection. Since Einstein's General relativity is torsion-free case, without dififculty by plugging the formula for christoffel connection we have
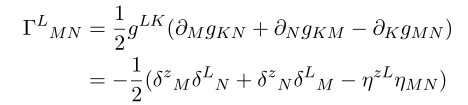
collecting non-vanishing terms we have
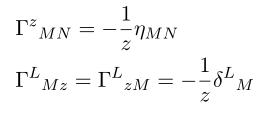
Now we can compute Ricci tensor and Einstein tensor.
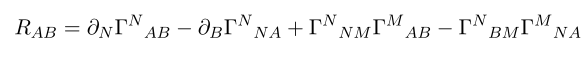
Plugging above formula for Ricci tensor we have
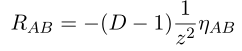
Furthermore we can see negative scalar curvature as follows.
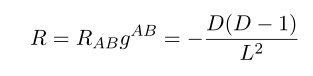
Now we can compute Einstein tensor.
Before first see Einstein equation
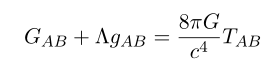
Since we are discuss no-matter case, the RHS is zero, thus we have
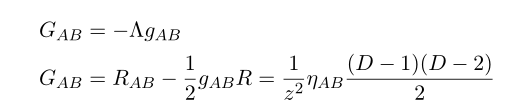
Re ordering this we can see it has negative cosmological constant as follows.
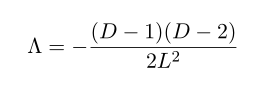
Finally starting from ads metric we have checked it has negative Ricci scalar and negative cosmological constant!