[Answer and winners] Mathematics × Programming Competition #3 [公佈得...

Mathematics × Programming Competition #3
Announcement of the Answer and Winners

For Chinese version please scroll to the bottom. 中文版請見文末。

Question

Ghost Leg (aka Amidakuji) is a tiny game which is used to create random pairings between two arrays. This is commonly used in lucky draws.

A ghost leg consists of vertical lines and horizontal lines. If there are N elements in an array, there would be N vertical lines and any number of horizontal lines. Horizontal lines should be touching two adjacent vertical lines. The rule of matching is by picking a vertical line at the top, and go downwards until you hit a horizontal line. Whenever you hit a horizontal line, travel along that horizontal line. Then continue to go downwards and repeat this process until you reach the other end.

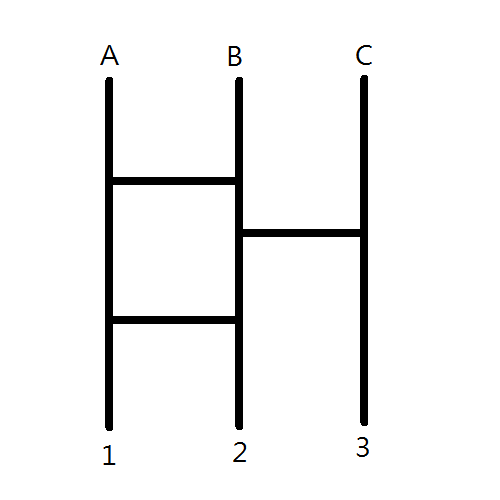
Consider this example on the left.

Obviously when there are no horizontal lines at all, the matched pairs would be {A,1}, {B,2} and {C,3}.

With the horizontal lines added, the matched pairs become {A,3}, {B,2} and {C,1}.

Make sure you understand this example before proceeding to the main question :)

Here comes the question. Consider the case N = 10. Given that when there are no horizontal lines, the matching pairs are {A,1}, {B,2}, {C,3}, {D,4}, {E,5}, {F,6}, {G,7}, {H,8}, {I,9}, {J,10}. What is the minimum number of horizontal lines to be added such that the final outcome would be {A,7}, {B,4}, {C,3}, {D,9}, {E,2}, {F,8}, {G,1}, {H,6}, {I,10}, {J,5}?

Answer 答案: 22

Consider the ghost leg graph below. It can be seen that adding a line essentially means swapping two adjacent numbers.

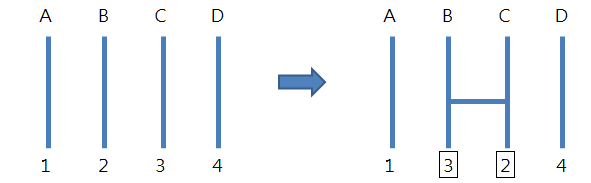
Therefore, our problem can be simplified as: what is the minimum number of adjacent swapping required to sort the array [7, 4, 3, 9, 2, 8, 1, 6, 10, 5] in ascending order?

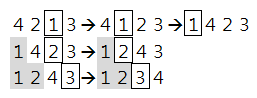
It turns out that the well-known bubble sort algorithm can swap an array in shortest number of steps if only adjacent swappings are allowed. For those who don't know bubble sort, we try to swap the array [4, 2, 1, 3] back to [1, 2, 3, 4] step by step:

Consider the smallest number '1' and try to move it to the leftmost position by adjacent swappings only. Fix '1' at its position and do not move it anymore.
Now move the second smallest number '2' to its correct position, just as what we did in step 1.

Therefore the corresponding ghost leg graph should be:

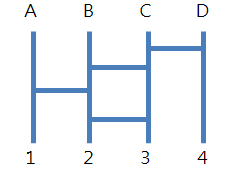
Similarly, for our array [7, 4, 3, 9, 2, 8, 1, 6, 10, 5], of course you can sort it by hand and count the number of inversions, but the best is to make use a bubble sort program:

JavaScript:


var a = [7, 4, 3, 9, 2, 8, 1, 6, 10, 5];
var count = 0;
for (var i=a.length-1; i>=0; i--){
    for (var j=a.length-i; j>0; j--){
        if (a[j] < a[j - 1]) {
            //Swap the numbers
            var temp = a[j];
            a[j] = a[j - 1];
            a[j - 1] = temp;
            // count number of inversions
            count++;
        }
    }
}
console.log(count);

Output: 22

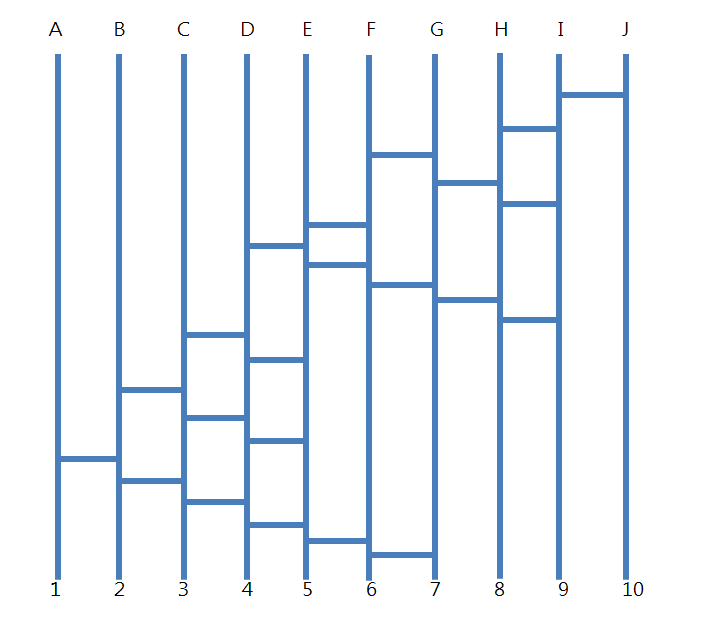
Here is the simplest ghost leg graph of our question: (hopefully I didn't make it wrong)

If you want to learn JavaScript, visit @adnanrahic 's blog to learn JavaScript!

The JavaScript Journey 1 - Values
The JavaScript Journey 2 - Arithmetic and Operators
The JavaScript Journey #3 - Logical Operators
The JavaScript Journey #4 - Special Values & Precise Comparisons

Mathematical proof

(You may skip this part if you are already confused ;) )

Formally speaking, the minimum number of horizontal lines required is the number of inversions in the array, which has the definition of:

two elements a_i and a_j form an inversion if a_i > a_j and i < j

To prove the statement above, we need to make use of two lemmas:

In an array, if every pair of adjacent numbers does not contain inversions, that array has been sorted.
Swapping any two adjacent numbers will reduce the number of inversions by at most 1.

The proof of the above lemmas is obvious and will not be stated here. From Lemma 1, we can see that if an array is not yet sorted, there must be 1 or more inversions for adjacent numbers. We can thus swap that pair of adjacent numbers so as to make the number of inversions in the array reduce by 1. This process can be repeated until all inversions for adjacent numbers are eliminated, which means the array has been sorted. Therefore we can conclude at least x adjacent swappings are required to make an array completely swapped, where x is the number of inversions in the array.

Now consider the algorithm of bubble sort again. Actually this algorithm is simply trying to reducing the number of inversions by 1 in each step, thus giving the simplest ghost leg graph.

Winners

Among 13 participants, there are 2 people who got the correct answers, thus getting the first and second prize accordingly. Thank you for all your participation and congratulations to the winners!

@carobetc @guyverckw @guyverckw @pizzachain @jbp @linuslee0216 @chl @jeffreytong @nanosesame @pakyeechan @wilkinshui @binbin88 @kitcat @thomaskikansha

Prize pool = Remaining prize from previous competition (1 SBD) + SBD payout of the announcement post (9.817 SBD) = 10.817 SBD

The winners and prizes have been tabulated below:

Winner	Prize	SBD
@guyverckw	First prize	10.817 * 30% = 3.245
@wilkinshui	Second prize	10.817 * 20% = 2.163

Prize carried forward = 5.409 SBD

Special announcements

The steemSTEM project (@steemstem) is a community-supported project aiming to increase the quality and the visibility of STEM (STEM is the acronym for Science, Technology, Engineering and Mathematics) articles on Steemit. Since one of the major aim of my competitions is to promote STEM which matches so well with this community, thanks to the steemSTEM team, starting from the next competition my posts will be curated by @steemstem so as to increase the prize pool.

Please support steemSTEM by following @steemstem, joining the chat channel and following the curation trail on Streemian! In order to further promote the use of the chat channel, I will stop announcing the time of next competition via a post. Instead I will announce the time in advance in the chat channel!

數學 × 程式編寫比賽 (第三回)
答案及得獎名單公佈

問題

畫鬼腳 是一個用以將兩個序列配對的小遊戲。畫鬼腳被經常應用在抽獎之中。

鬼腳圖由直線及橫線組成。若一序列有N個項目，該鬼腳圖則共有N條直線及任何數量的橫線，且橫線必須連著相鄰的直線。配對規則為選取其中一個頂點，然後向下移動，直至遇到橫線。遇到橫線的時候需要跟著橫線行走，然後繼續向下移動，並重覆以上步驟，直至到達另一端。

試參考左側例子。

當圖中完全沒有橫線，明顯地配對結果為 {A,1}、{B,2}及{C,3}。

加上橫線後，配對結果便變成 {A,3}、{B,2}及{C,1}。

繼續閱讀問題前請確保你已完全明白這個例子 :)

現在終於來到問題部分了。考慮N = 10。已知當鬼腳圖中完全沒有橫線，配對結果為 {A,1}, {B,2}, {C,3}, {D,4}, {E,5}, {F,6}, {G,7}, {H,8}, {I,9}, {J,10}。求最少需要加上的橫線數目使得配對結果為 {A,7}, {B,4}, {C,3}, {D,9}, {E,2}, {F,8}, {G,1}, {H,6}, {I,10}, {J,5}。

答案: 22

考慮下圖之鬼腳圖。我們可見加上一條橫線可令兩個相鄰的數字對調。

因此問題可被簡化為：如要將序列[7, 4, 3, 9, 2, 8, 1, 6, 10, 5]由小至大排序，最少需要多少次相鄰數字的對調？

答案是一個名為「冒泡排序」的方法可以讓我們用最小步數將一序列排序。如果你不清楚甚麼是「冒泡排序」，可參考以下由４２１３轉成１２３４的例子：

我們首先考慮最小的數字，即１。現在嘗試將１移至最左，完成後不再改變１的位置。之後將第二小的數字（即２）移到其正確位置，如是者直至所有數字均到達其目的地。

因此相應的鬼腳圖如下：

同樣地，我們可以用「冒泡排序」找出這條問題的答案。當然你可以人手進行「冒泡排序」，但較佳的方法便是編寫程式：

JavaScript:


var a = [7, 4, 3, 9, 2, 8, 1, 6, 10, 5];
var count = 0;
for (var i=a.length-1; i>=0; i--){
    for (var j=a.length-i; j>0; j--){
        if (a[j] < a[j - 1]) {
            //Swap the numbers
            var temp = a[j];
            a[j] = a[j - 1];
            a[j - 1] = temp;
            // count number of inversions
            count++;
        }
    }
}
console.log(count);

輸出: 22

因此相應的最簡鬼腳圖如下：（希望我沒有畫錯吧）

如果你想學習JavaScript，不妨參閱@adnanrahic的文章！

The JavaScript Journey 1 - Values
The JavaScript Journey 2 - Arithmetic and Operators
The JavaScript Journey #3 - Logical Operators
The JavaScript Journey #4 - Special Values & Precise Comparisons

數學證明

（如果你已經感到頭昏腦脹，可考慮跳去此部分）

嚴格來說，最小的橫線數目為終點處數列中的「逆序對」數目，而「逆序對」則定義為一數列中兩個不按順序排列的數字。例如４２１３當中共有４個逆序對，分別為４及２、４及１、４及３、２及１。

證明方面，我們需要用到２個引理（Lemma），引理的證明頗為易見，我們不在此述。

引理１：若一數列中的相鄰數字沒有任何逆序對，該數列則已按順序排列。

引理２：兩個相鄰數字的互換只會令逆序對的數目最多減少１。

由引理１可見，若數列未按順序排列，數列中必有相鄰逆序對，我們可先把其互換位置，令逆序對的數目減少１。此動作可不斷重覆，直至所有相鄰逆序對消失，屆時數列則已按順序排列。因此，我們需至少進行x次相鄰數字的互換方能令一數列順序排列，x為數列中逆序對的數目。

現在再次回想我們在上方所述的冒泡排序，其實此方法的每一步正正令一個逆序對消失。因此冒泡排序得出的鬼腳圖便是最簡鬼腳圖。

得獎者

在13個得獎者之中，有2人答對，因此他們分別獲得第一及第二名獎項！多謝大家的熱烈參與，以及恭喜所有得獎者！

@carobetc @guyverckw @guyverckw @pizzachain @jbp @linuslee0216 @chl @jeffreytong @nanosesame @pakyeechan @wilkinshui @binbin88 @kitcat @thomaskikansha

是次獎池 = 上回比賽剩餘獎金 (1 SBD) + 公佈比賽的帖文的SBD收入 (9.817 SBD) = 10.817 SBD

下表顯示得獎者及其所得獎金：

得獎者	獎項	SBD
@guyverckw	第一名	10.817 * 30% = 3.245
@wilkinshui	第二名	10.817 * 20% = 2.163

下回比賽獎池現有 = 5.409 SBD

特別宣佈

steemSTEM項目（@steemstem）是一個由steemit社群支持的項目，旨在宣傳STEM（STEM是科學，技術，工程和數學的首字母縮略詞）。由於我的比賽的主要目的之一是促進STEM，從下一場比賽開始，我的帖子將由@steemstem提供upvote以增加獎池，在此特別感謝steemSTEM團隊。

請通過以下方式來支持steemSTEM：追蹤@steemSTEM，加入聊天頻道和加入Streemian！為了進一步推廣聊天頻道的使用，我將不再透過發文來宣布下一場比賽的時間，我會在聊天頻道中提前公佈比賽時間！

[Answer and winners] Mathematics × Programming Competition #3 [公佈得獎名單] 數學 × 程式編寫比賽 (第三回)

Mathematics × Programming Competition #3Announcement of the Answer and Winners