Question
(Difficulty: 6/10)
In a country, each of the citizens has a 6-digit ID number. For example, 077493 is a valid ID number. Now the country holds a lucky draw: citizens having all the three numbers '6', '8' and '9' in the ID number can have the chance of slapping the Chief Executive. For example, 066189 can slap the Chief Executive but 691674 cannot.
What is the probability that a citizen can slap the Chief Executive?
Assume:
- There are not more than 1,000,000 people in this country
- Each citizen has a unique ID number
- ID number are randomly generated for each citizen, i.e. the first man in this country may have an ID 729412

Solution
The probability we want to find is Pr(has 6 AND has 8 AND has 9)
Finding this may not be easy, so let's consider its opposite: Pr(no 6 OR no 8 OR no 9)
Let's consider the Venn Diagram below, which is a great tool to solve probability problem.
Venn Diagram
Let's consider three events: no 6, no 8 and no 9. Can we break down the event of {no 6 OR no 8 OR no 9} into {no 6} + {no 8} + {no 9}? No! Because in this way we would have double-counted some events, such as {no 6 AND no 8}.
Now let's draw a Venn Diagram, which helps us to visualize the events.
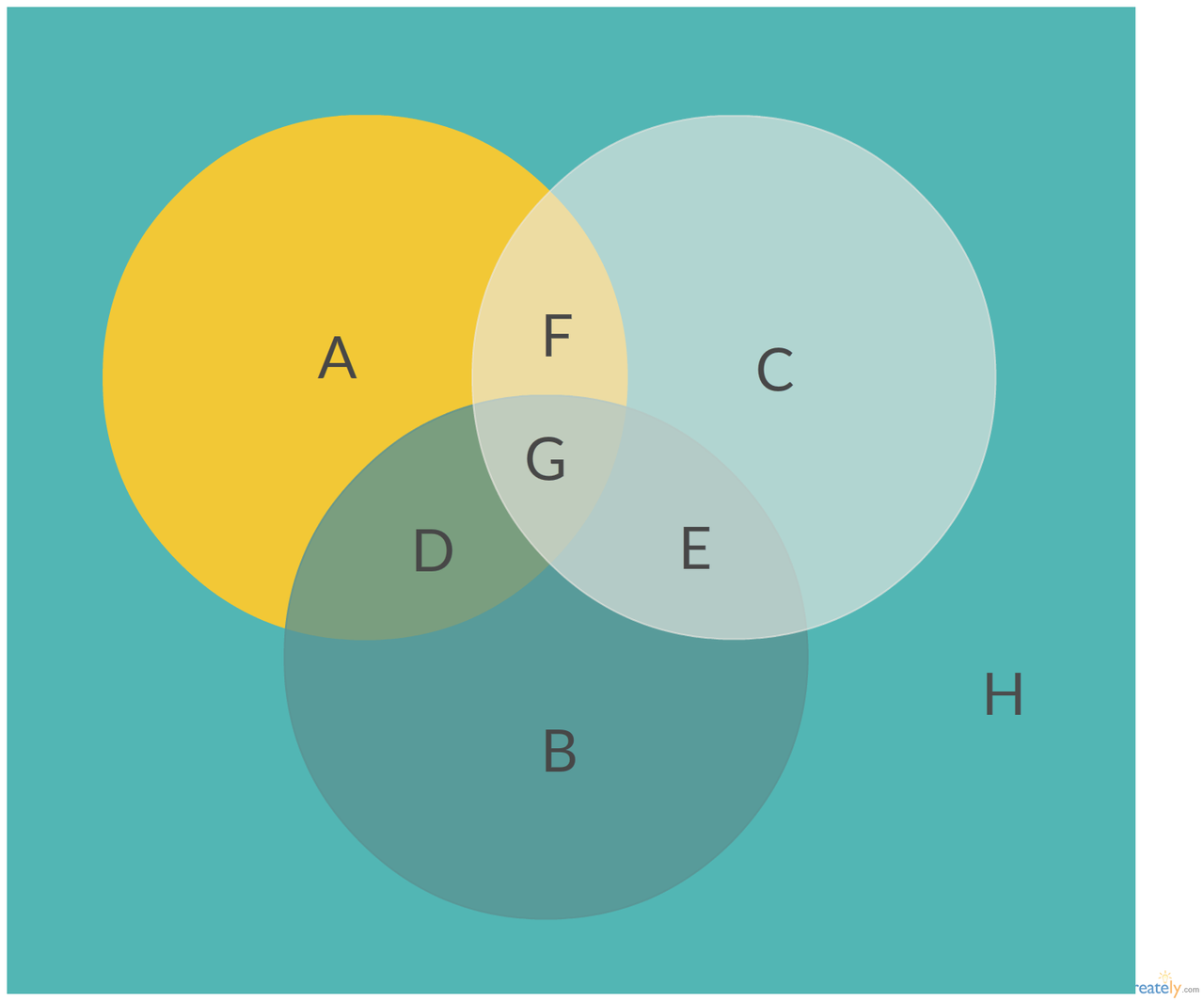
We now have 3 circles, which represents the three events: {no 6}, {no 8}, {no 9}. However these three circles have some intersection areas, like D, E, F and G.
Here is a list of the meaning of each collection of areas:
- A+D+F+G: {no 6}
- C+E+F+G: {no 8}
- B+D+E+G: {no 9}
- F+G: {no 6 AND no 8}
- D+G: {no 6 AND no 9}
- E+G: {no 8 AND no 9}
- G: {no 6 AND no 8 AND no 9}
- A+B+C+D+E+F+G: {no 6 OR no 8 OR no 9}
- H: {has 6 AND has 8 AND has 9} What we want!
Therefore, what we need to find is Pr(H), which can be done by finding the area of (A+B+C+D+E+F+G) first.
Here is our final result (you can try to verify it by considering the areas that these events represent):
Pr(no 6 OR no 8 OR no 9) = Pr(no 6) + Pr(no 8) + Pr(no 9) - Pr(no 6 AND no 8) - Pr(no 6 AND no 9) - Pr(no 8 AND no 9) + Pr(no 6 AND no 8 AND no 9)
This is also known as the inclusion-exclusion principle.
Calculations
Pr(no 6) = Pr(no 8) = Pr(no 9) = 0.9^6
Pr(no 6 AND no 8) = Pr(no 6 AND no 9) = Pr(no 8 AND no 9) = 0.8^6
Pr(no 6 AND no 8 AND no 9) = 0.7^6
Therefore Pr(no 6 OR no 8 OR no 9) = 0.92554
Finally we have the required answer = 1 - 0.92554 = 0.07446
Congrats to @kelkoo !
Previous posts
Math challenge #1 - Find the remainder!
Math challenge #2 - Find the value of these recurring square roots
Math challenge #3 - Find its length!
Interested in Math puzzles? Follow @kenchung, upvote and resteem! :)
