Homer threw a baseball to Bart. Like that:

Notice that at the moment in time depicted on the image, the ball is located at a certain fixed position in space. While it is being in that fixed position, it is certainly not moving. Because, as we know, an object in a fixed position must be fixed, by definition, right?
But this logic must then be true for any timepoint. Indeed, no matter when you look at the ball, it must always be "frozen" at a certain fixed position in space.
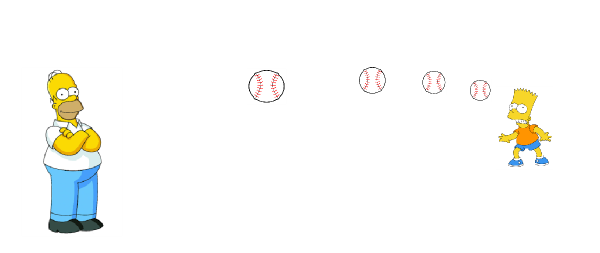
Now, if the ball is "frozen" at all points in time, there are no observable moments when it moves. We must therefore conclude that the ball, in fact, never moves at all!
This is the third famous paradox of Zeno, commonly known as the "Arrow paradox" (because in the original story Achilles was shooting an arrow rather than throwing a baseball, of course). While the first two Zeno's paradoxes are mathematical sophisms, which can easily be resolved with some proper calculus, this one is very different.
Rather than being just a mathematical curiosity, it is primarily a philosophical question about the nature of time. What is time if not a collection of fixed snapshots of the universe we observe around us? And if it is, how and why are these snapshots changing one into another so that things seem to move?
For Bart and Homer in the cartoon, we actually know the answer: it is the video rendering algorithm, which continuously replaces each frame with the next one. If Bart and Homer were characters of a computer game instead, the state of their world would be updated by a CPU running the program. But what about us and the real world? Is our time discrete or continuous? Are we all just part of an exciting movie with someone changing frames? Is it all a big computer simulation? How and why do things change around us? What is time, after all?
Take some time to think about it.
For other sophisms check out this list.
