"CLIMBING A MOUNTAIN WITH TRIGONOMETRY" ~ © Tiffany E. Reed

I dearly love mountains and have admired and studied the mountains in my area carefully. Several times, I tried to figure out which, of several visible peaks, might be the highest mountain of those nearby.

I know the name of the mountain, its elevation, location, and have been there numerous times. However, when at a distance from it, I could never determine with any certainty which peak it was among all those visible. I finally arrived at the conclusion that it might be hidden behind another mountain. That was just a hunch, though.

Part of my formal education at the collegiate level involved some pre-engineering courses — including Physics and Applied Trigonometry, among others — and these could help me prove my hunch in a mathematical manner. So here it is, safely etched into the blockchain so I don't lose the numbers/results if I should want to revisit them later. Also, this technique can be used by anyone to demystify a similar situation.

The website windy.com is good for showing weather conditions anywhere on Earth. It is also good for showing a simple, non-cluttered view of an area with mountain peaks marked:

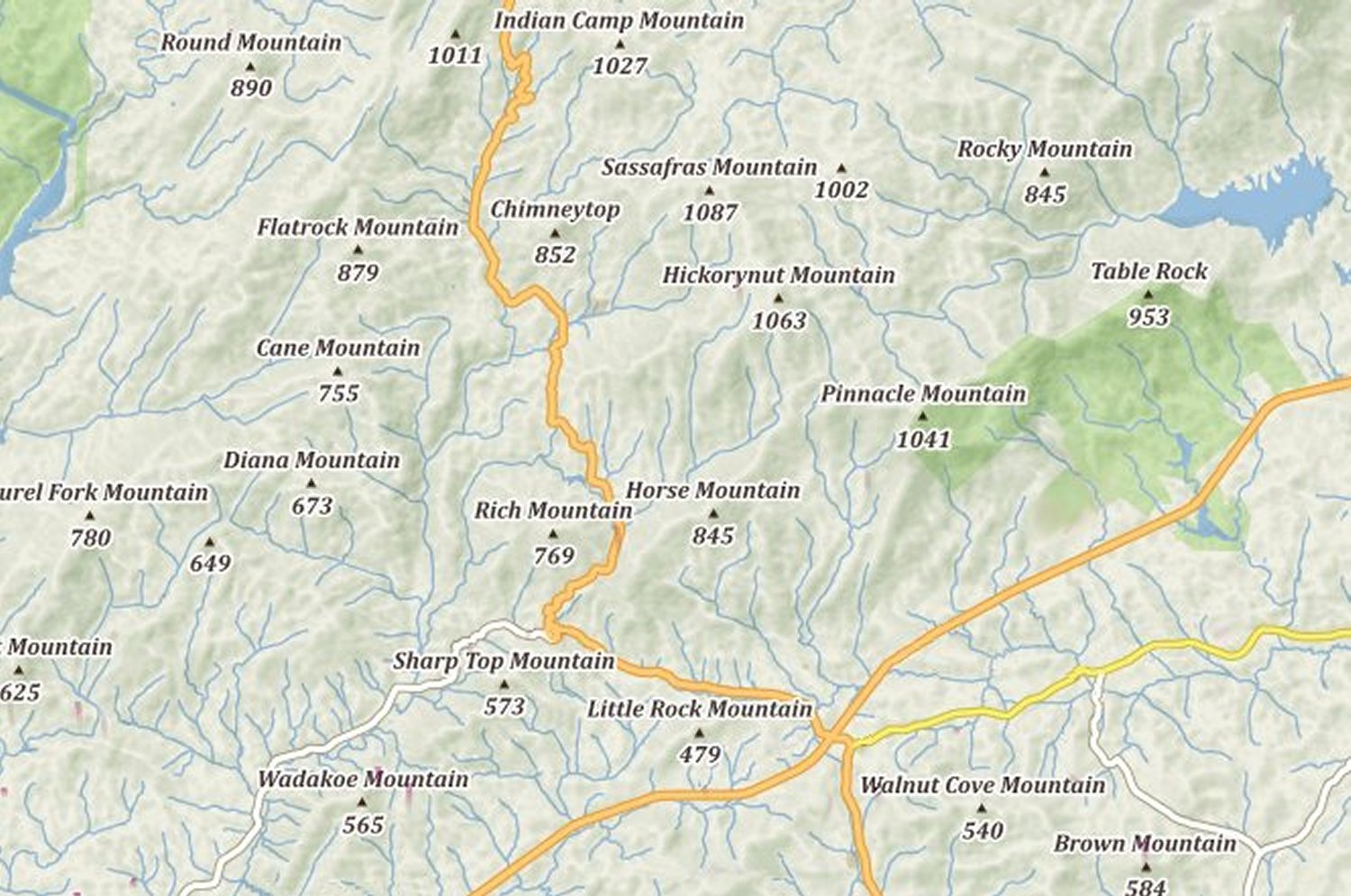
I made note of the mountain peaks which were of noticable size (purple) to the left and right of the target mountain (in blue):

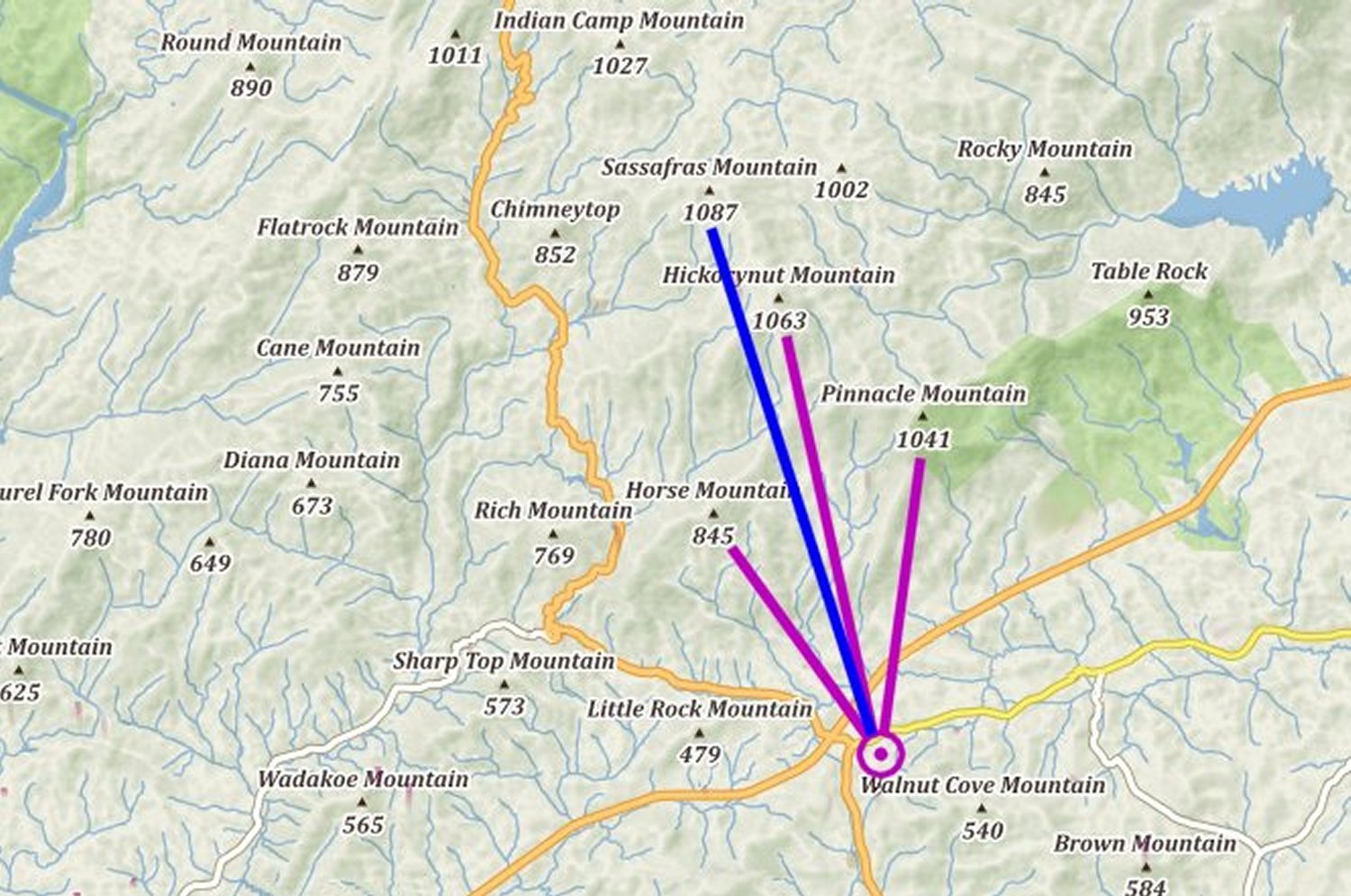
Here is a photograph looking towards the same mountains, about 15 minutes from the house where I am currently living:

To begin the study, I needed to know how far the mountain peaks were from my chosen vantage point. A very useful website for travelers, joggers, cyclists, and pedestrians is GMAP-Pedometer, which can determine distances along roadways. As an added benfit, it can also calculate straight-line distances as well, so I used this feature to calculate the line-of-sight distance to the mountain peaks. For this purpose, I chose to display topographical maps from the United States Geological Survey (USGS) for better accuracy.

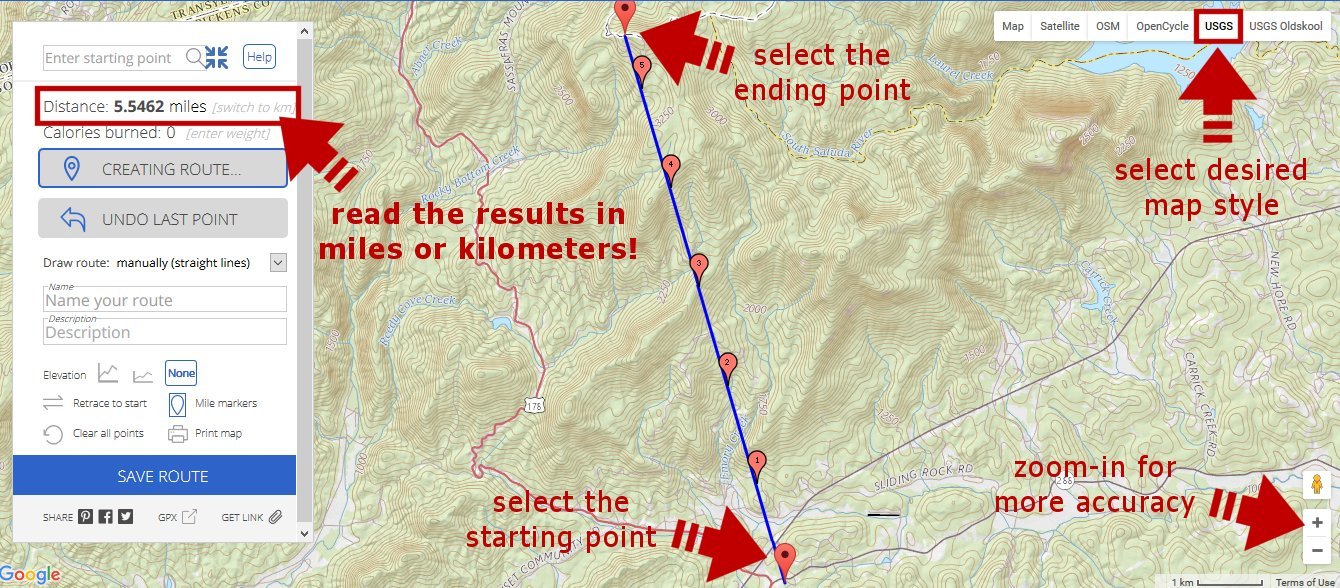
The applied trigonometry technique follows for anyone who wants to replicate it.

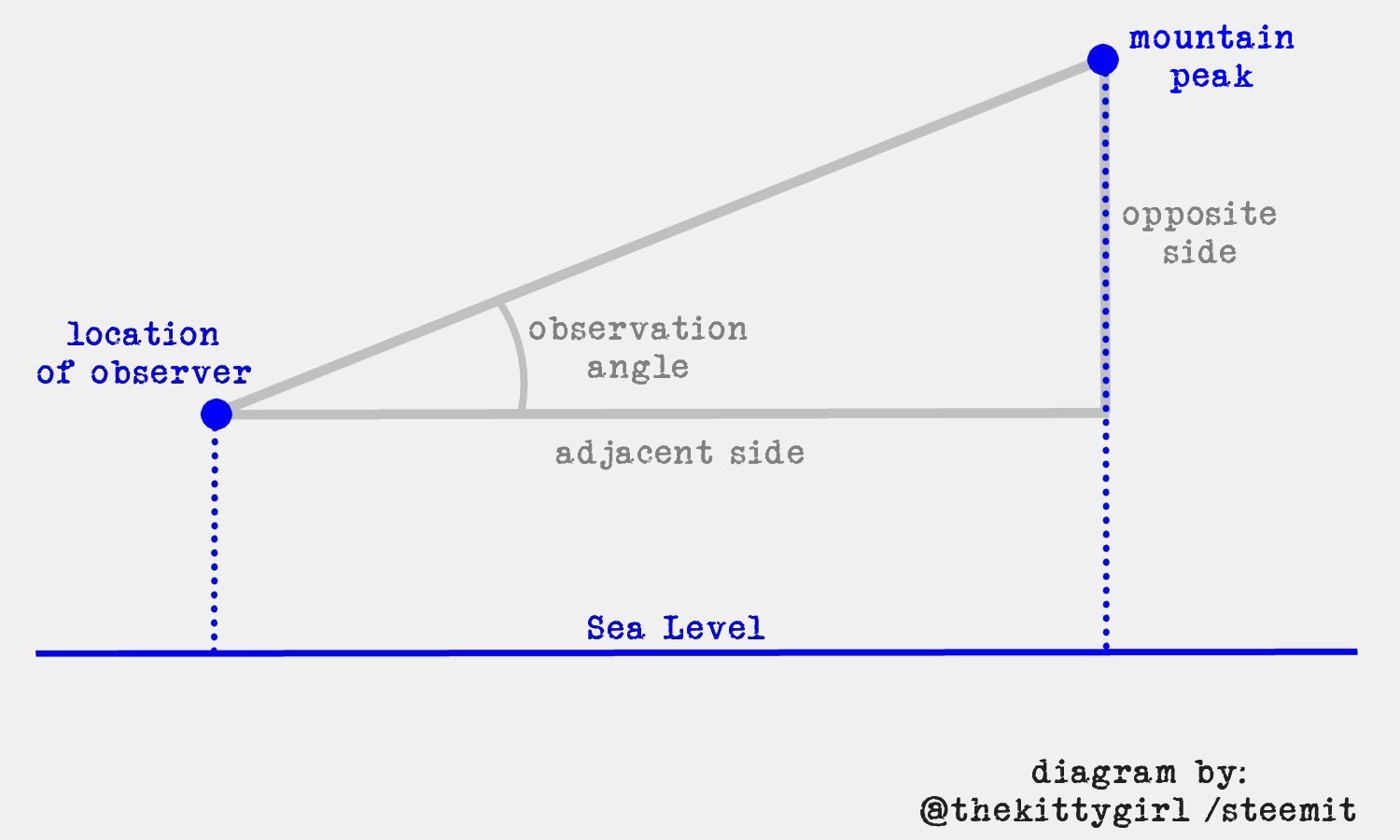
Calculate the elevation of your observation point from a topographic map.
Draw a line on the topographic map from your location to the mountain peak you think is hidden. Then, calculate the linear distance to that point beneath the peak of the mountain. That will be the "adjacent" side (a1) of a first right triangle.
Subtract the elevation of your observation point from the elevation of the peak. That will be the "opposite" side (o1) of the first right triangle.
Be sure both of the above measurements are in the same units (feet, meters, etc.). e.g., If you're measuring the distance to the mountain in miles and the height of the mountain in feet, you will need to convert "miles" to "feet" before doing the computations.
Calculate the arctangent of o1/a1 in degrees.

Or, expressed as mathematical formulae:

peak1 = nominal_elevation1 - your_elevation
angle1 = arctan ( peak1 / distance1 )

Repeat the steps for the second peak, the one closer to you which you think is hiding the first peak.

Or, expressed as mathematical formulae:

peak2 = nominal_elevation2 - your_elevation
angle2 = arctan ( peak2 / distance2 )

If the angle to the closer peak (angle2) is greater than the angle of the distant peak (angle1), then the distant peak is hidden, otherwise it should be visible.

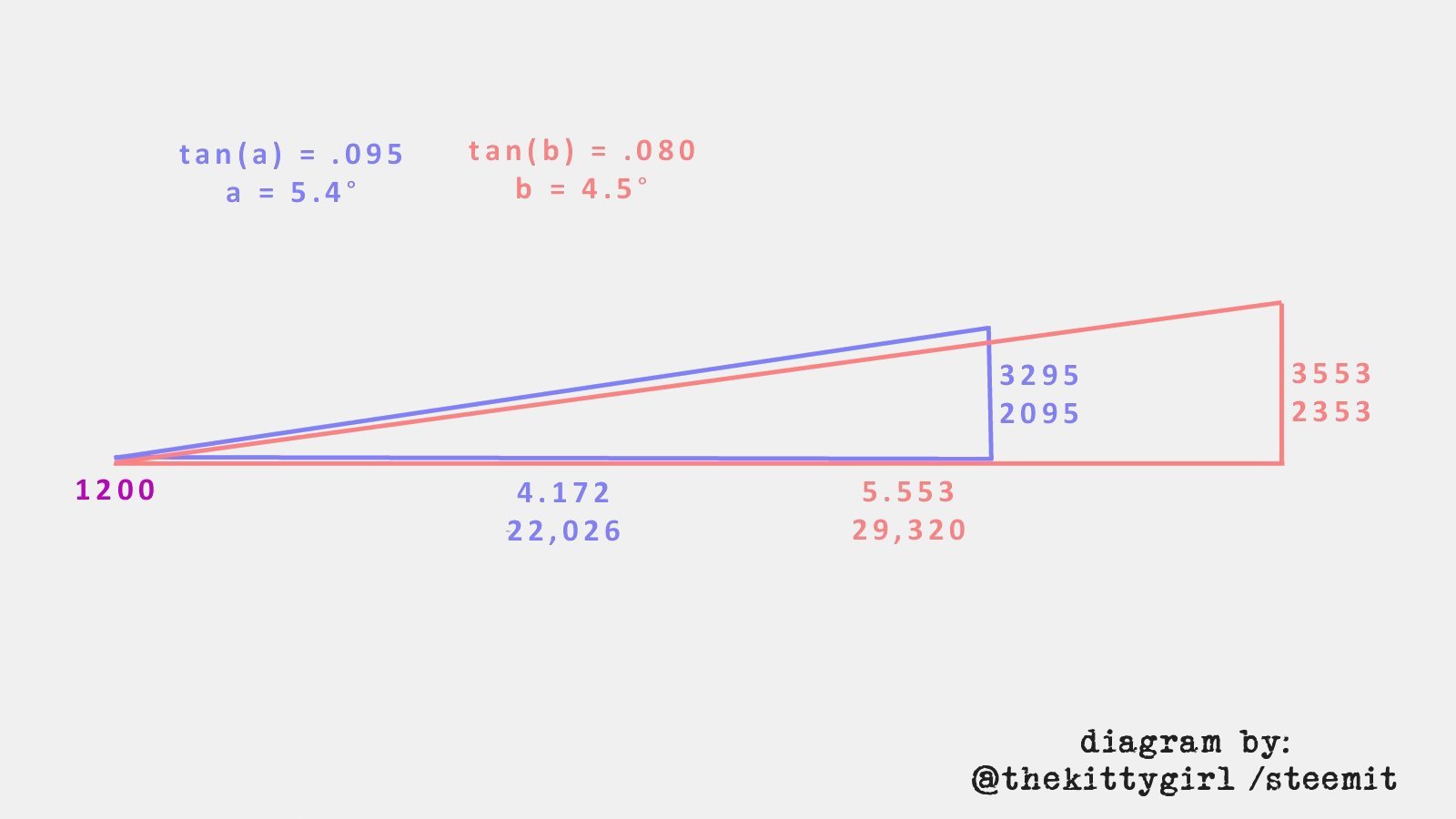
And YES, the higher-but-further peak in my case is, indeed, hidden behind the lower-but-closer peak! My hunch was correct!

Since the distances and elevations in this particular example are relatively small, the curvature of the Earth should be negligible. However, to double-check that assumption, I turned to the Internet.

Several sources concur that the curvature of the Earth is roughly: 8 inches per mile squared.
[one, of many, sources]

The mountain is 5.5 miles (8.85 km) distant, which equates to a total change of 20.17 feet (6.15 m) due to the curvature of the earth. So, the peak of the mountain would appear to be that much lower than its already perceived height, and at a distance of 5.5 miles, I consider that to be a virtually negligible ratio at: 6.946 x 10^-4.
[source, with equations]

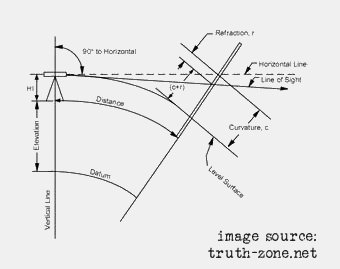
This diagram shows some of the geometric relationships involved in such calculations relating to the curvature of the earth:

I once used techniques such as this every day in solving problems at my job, but with products my company was designing and manufacturing, not with mountains. It was so cool to once again find a use for the Applied Trigonometry I took in college, after not working in an Engineering or Information Technology environment for many years. 😊