This is the second of TraderSharpe's maths problems. The biggest challenge here is to not sound like I'm just copying him, since he's already answered the question himself in other posts. So, here goes. The problem in full:

For problem a), we want to show that 2 ÷ ¼ is the same as 2 x 4. The left hand side is asking us how many quarters are in two. So, let's start with two circles:
We can find how many quarters these two circles contain by dividing them into quarters, and then counting the quarters.
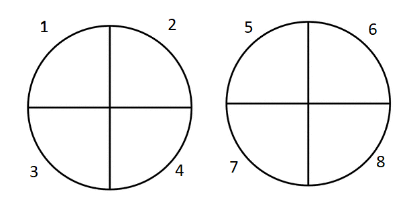
We have 8 quarters. But, looking at this second picture, we can see that by dividing each circle into four, we have inadvertently made two groups of four, which is a way of expressing 2 x 4, the right hand side of equation a)!
So 2 ÷ ¼ = 8 = 2 x 4
Problem b) can be treated similarly. It's asking how many 2/3 are in 6, so let's start with six circles.
And then divide these circles into thirds.
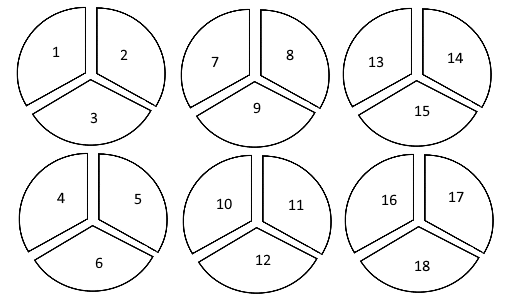
There are 18 thirds (18/3) in six circles, but this isn't yet quite what we want. We want to know how many 2/3 (two thirds) are in six items. So, let's rearrange our 18 thirds like this:
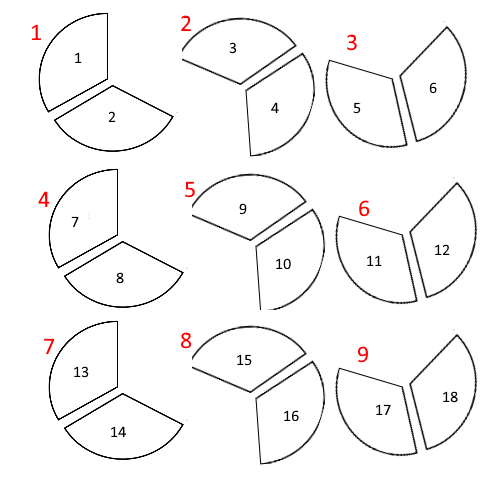
Now in each group there are two thirds. Counting these groups (in red), we can see that there are nine groups of 2/3.
To show that this is equivalent to the right hand side of equation b) isn't as straightforward as it was in a) because dividing the circles into groups of one quarter conveniently gave us groups of four ones (4/1). In the case of equation b) the right hand side requires us to convert our circles into halves. We have seen that 6 ÷ ⅔ = 9, so now we need to show that
6 x ³/₂ = 9 as well.
So, let's start with 6 groups of ³/₂ (three halves):
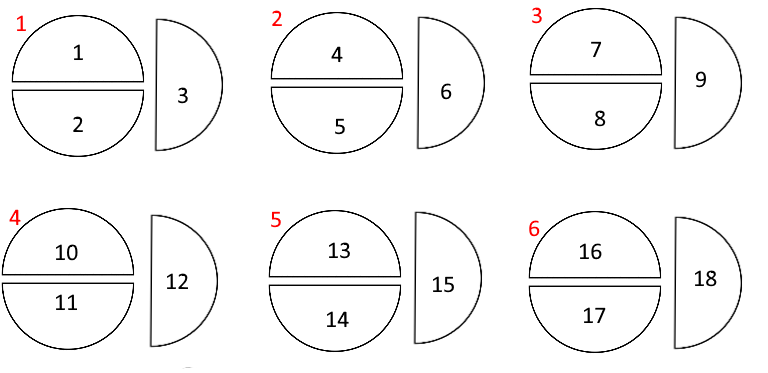
I've numbered the halves in black so it's easy to keep track of how many there are, as well as numbering the groups in red.
Now we need to see how many whole circles we can make out of what's here. So, let's just turn the odd semi-circles around and pair them with the one above/below them:
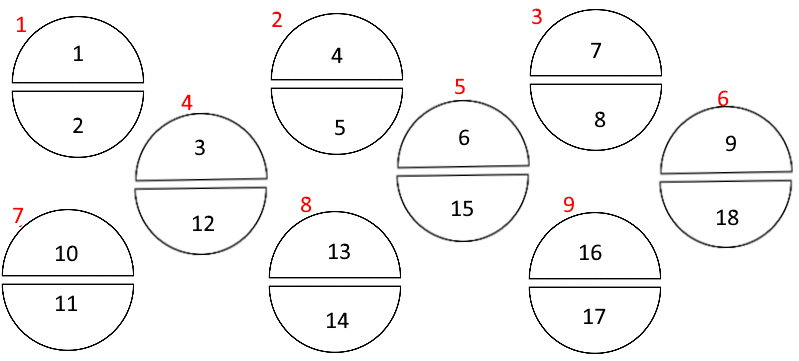
and there we go: 9 whole circles. The number 9 is the same value as we got for how many ⅔ we can make out of 6.
6 ÷ ⅔ = 9 = 6 x ³/₂
Problem c) 9 ÷ ³/₂ = 9 x ⅔ is almost the same as problem b). Whereas in problem b) we divided by ⅔ on the left and multiplied by ³/₂ on the right, in problem c) we have ³/₂ on the left and ⅔ on the right.
So, let's start with 9 circles and find out how many groups of ³/₂ we can find. Oh look, we have a convenient diagram above with 9 circles divided into halves! What happens when we rearrange those into groups of ³/₂?

Yup! We have been here before, just going through the steps in reverse. So 9 ÷ ³/₂ = 6 now we need to show that 9 x ⅔ = 6 as well.
Here is our handy recycled diagram showing 9 groups of ⅔

Rearrange these into whole circles:

Ta da! Six whole circles appear again. So 9 ÷ ³/₂ = 6 = 9 x ⅔
Thank you to @tradersharpe for continuing to hold competitions despite the mathapy!
