The most important class in my undergraduate Mathematics department was not Calculus or any of the higher level classes: it was a class called Fundamentals of Abstract Mathematics. This was a gateway class from the 200 level math classes to the 300 level classes that taught how to think like a mathematician and built the foundation for upper level mathematics such as Abstract Algebra, Real Analysis, and Complex Analysis. A corollary class to this exists in the philosophy department called An Introduction to Logic.
In this blog, we’ll go through the necessary background work so that we can start proving beautiful mathematical theorems.
One of my favorite proofs typed out in LaTex because nobody can read my handwriting:

we will step through and dissect this proof in a later blog after we build up the necessary background knowledge to do so.
I find this process and way of logically proving things an absolutely essential weapon in your mathematical arsenal; but this is not only important for mathematicians, thinking logically is the very foundation of making strong arguments and is necessary for everyone. I want to help increase mathematical fluency on steemit and decrease the fear of mathematics that many people have.
Propositions
A proposition is a sentence that is either true (T) or false (F). It has exactly one truth value: T or F
examples of propositions:
(a) 1+1 = 3
(b) Humans will discover extra-terrestrial life before the year 2050.
(c) Barack Obama ate cereal for breakfast on the day he graduated high school.
(a) clearly has the value of false because we know 1+1=2, not 3.
We possibly won’t know the answer of (b) until the year 2050 at latest, but it’s truth value will be established one day.
There might not be any way to determine if (c) is true or false, but nevertheless, each of the above is either true or false and is a proposition.
The following are examples of sentences that are not propositions:
(d) Please study mathematics.
(e) What is your name?
(f) This sentence is false.
(e) is a command/request, it doesn’t have a truth value.
(f) is a question, it doesn’t have a truth value.
(g) is an example of a sentence that is neither true or false but is instead referred to as a paradox. If (g) is true, then by its definition it is false. But if (g) is false, then “this sentence is false” is false, which means the sentence is true. Unlike Schrodinger’s Cat and quantum superpositions, a sentence cannot be simultaneously true and false, so this is a contradiction, and it has neither the value of true or false.
Propositions can be combined into compound propositions that use logical connectives between simple propositions to form more complex sentences. For instance, “Humans will discover extra-terrestrial life before the year 2050 and 1+1=3” is a compound proposition formed by connecting two propositions, namely (a) and (b) from above, with the word “and”.
Symbols and Common Notation
Rather than writing out each sentence in English, we can translate English sentences to symbolic form. Represent each proposition with a letter, and then use connectives such as “and”, “or”, and “not” to form compound propositions.
Let’s symbolically refer to the following two propositions as P and Q:
P = “Today is Monday”
Q = “It is Raining in Irvine, California”
In this case, P has the value true (it is Monday), and Q has the value false (it never rains in Irvine, California). Using symbols helps shorten the later mathematical proving process.
Given propositions P and Q, we have the following connectives:
And: the conjunction of P and Q, denoted “P ^ Q” is equivalent to the proposition “P and Q”. P ^ Q is true when exactly both of P, Q are true. If at least one of P, Q are false, then P ^ Q is false.
Or: the disjunction of P and Q, denoted “P v Q” is equivalent to the proposition “P or Q”. P v Q is true when at least one of P, Q are true. P v Q is false when both P and Q are false.
Negation: the proposition “not P” is represented as ~P. ~P is true when P is false, and ~P is false when P is true.
So using our example from before where P = “Today is Monday” and Q = “It is raining in Irvine, California”, we can come up with values for P^Q, PvQ, ~P, and ~Q
P^Q is false, because Q is false and we need both P and Q to be true for P^Q to be true.
PvQ is true. Since P is true, then the condition of at least one of them being true is met, so PvQ is true.
~P is false: Since P is true, then ~P is false.
~Q is true because Q is false
So, it is false that “Today is Monday and it is raining in Irvine”. But it is true that “Today is Monday or it is raining in Irvine”. It is also true that “it is not raining in Irvine”.
Propositional form
An important distinction must be made between propositions and propositional forms. “It is raining in Irvine” is a proposition with a single truth value (F), while the propositional form (P^Q) which may be used to represent a sentence symbolically has no base truth value: it obtains a value of T or F when P and Q are assigned values of T or F.
Truth Tables
Mathematicians and logicians use truth tables to discover when propositional forms are equivalent to each other or when a complicated statement has a true or false value.
Here are the truth tables for P^Q, PvQ:
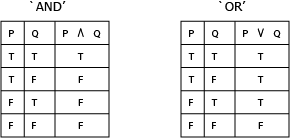
Since each P and Q can have 2 different values (true or false), there are 4 total possibilities: true true, true false, false true, false false. The trick to exhausting all possibilities in a truth table is to list P as T twice then F twice, and alternate Q every other one.
P^Q is true only when both P and Q are true, and P v Q is false only when both P and Q are false.

When P is true, ~P is false. When P is false, ~P is true.
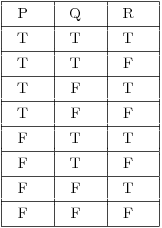
In the first image, since there are 2 propositions, there are 4 lines. In the second image, since there is 1 proposition, there are 2 lines. In general, when there are N propositions, there are 2^N lines. So if there were 3 propositions, there would be 2^3 = 8 lines in our truth table. If there were 4 propositions, there would be 2^4 = 16 lines.
When making an 8 line truth table with variables P, Q, R, we would first list P true 4 times then false 4 times: TTTTFFFF, list Q true 2 times then false 2 times then repeat: TTFFTTFF, and alternate R every other one TFTFTFTF. This gives us the 8 possibilities: TTT, TTF, TFT, TFF, FTT, FTF, FFT, FFF.
Equivalence
Two propositional forms are equivalent if and only if they have the same truth table.
A truth table shows that ~(P^Q) is equivalent to (~P) v (~Q). This is known as one of De Morgan’s Laws and we will introduce it next blog
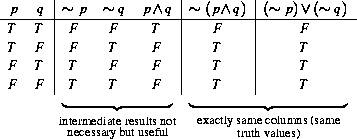
Once again, notice the distinction between propositions and propositional forms. Propositions have only one truth value so we don’t look at truth tables to decide their equivalence. Propositional forms are neither true nor false; they have the value true for some assignments and the value false for other assignments. So o decide equivalence of propositional forms, we compare truth tables.
Tautologies are propositional forms that are always true for every assignment of truth values to their components. The easiest example is P v ~P. Either P is true or ~P is true, but P v ~P is always true.
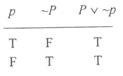
A contradiction is the negation of a tautology. For instance ~(P v ~P) is a contradiction: it is always false.
Summary/Recap:
-Propositions are sentences that can be either true or false.
-Compound propositions are finitely many propositions connected by logical symbols
-Propositional forms are expressions involving finitely many logical connectors and letters.
-a paradox is a sentence that leads to a self-contradictory conclusion.
-Use letters such as P, Q, R, S to shorthand propositions
-"P and Q" = P^Q
-"P or Q" = P v Q
-"not P" = ~P
-truth tables with N propositions have 2^N lines
-When two compound propositional forms have identical truth tables they are equivalent
-Tautologies are always true
-Contradictions are the negation of tautologies.
