Fermat’s theorem (stationary points)
In mathematics, Fermat's theorem states the local extremum of the function (Local maximum or Minimum) has a slope equal to 0. This is Yet another calculus theorem that is easy to understand and prove.
I used this theorem to show the proof of Rolle's theorem which you can read about here
Let us look at the theorem intuitively.
As we can see each tangent line changes to a less steep slope as it gets closer and closer to the highest maximum point. Here is a graphical illustration here:
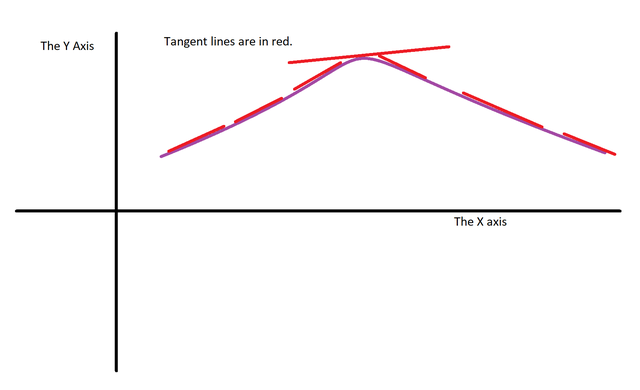
One can test this in the real world by using a ruler (or something straight and flat) and a ball (or anything with a nice round and steadily smooth like a balloon etc.). You need to lay the ruler flat on the ball and slide all the way up to the highest point. Notice how the rulers angle becomes less steep as you slide it closer and closer to the highest point. Here is a graphical illustration on how the experiment will look like.

Please note the line is the flat ruler. It only looks like a line due to the angle of the ruler
It makes all sense if we think of what happens in a curve. In a curve with a local extremum we can see that the line is bending/ turning in the opposite direction. It must start and gradually change its slope in that opposite direction. Since the curve is continuous and its derivative is also a continuous function thus it gradually gets closer to the x-axis until it intercepts (turns 0) then it switches symbol values. Here is once again a graphical illustration of this relationship of the original function and it’s derivative.
Here is a parabola:
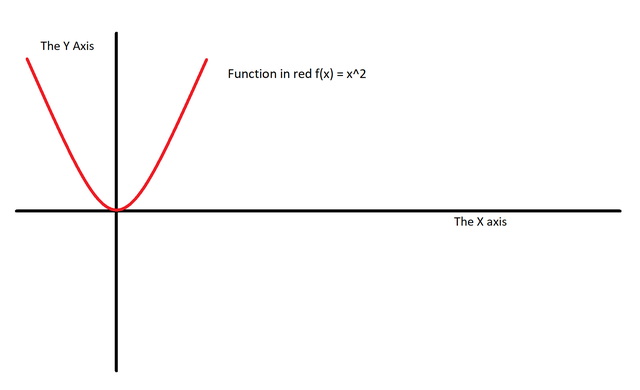
Here is the parabola’s derivative:
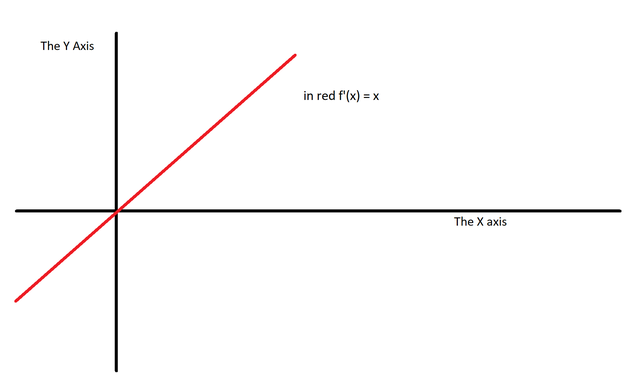
The parabola’s lowest point is at x = 0 and y = 0. Its derivative is also at that point. Thus, its slope is = 0.
Now it is time for the mathematical proof:
For this proof we need to use the extreme value theorem which states that if a function is continuous on an interval of A and B (written mathematically as [A,B] ) and it is differentiable on the interval A and B excluding A and B itself (written mathematically like this (A,B). ), then it has an absolute max/min.
Now for our proof we assume the following:
The function is continuous on the interval A and B, [A,B].
It is differentiable on the interval A and B excluding A and B, (A,B).
It has at least one local extrema
Now we must address two cases, one for a local maximum and one for a local minimum.
So for case one:
*Please note that I had issues printing the mathematical symbols on steemit so I took a screenshot of the mathematical proof! but it is my own work!


thus our case is proven.
The same logic applies for our other case.
This was used in my Rolle's theorem which you can read here
As always thanks for reading!
what do you think? leave a comment down below. Do not forget to upvote, Resteem and follow my blogspot!
check out more posts Here
Please Resteem It would really help my blog!


