Note: What I am going to post is mathematically controversial. There has been a debate between mathematicians for ages on this topic. But with this mind…I find this whole topic interesting! I will be making two parts (there is allot to discus). This is part one, In this part I will discuss ways to calculate sum to infinitys that diverge. Please skip to the head: “Time for the mathematics” if you do not want to read about a bit of history or about how these sums works.
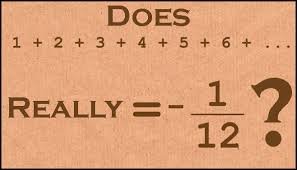
As you may have seen in the title I stated that the sum of all natural numbers (Sn = 1+2+3+4+5…) is equal to -1/12! This result has been adopted in quantum mechanics for their equations and it helps to describe quantum phenomena! I can personally understand why this result fit in the quantum mechanics world, both of the those things does not make any sense!

But all jokes aside, if you keep a mathematical open mind on the process of how it is calculated, you might find some sense in this result!
Some things you need to know before we start!
certain sums of infinity do give sensible values, and the average person would say that it makes sense! We call these types of sums convergent. Here is a classic divergent row of sums:
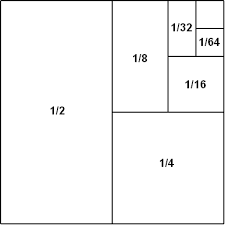
Sn =1+½+¼+⅛+...
Each time you add half of the previous thing you added. This means if Sn goes on to infinity, you will find that
Sn= 2
Here is a picture graphically showing what is happening
But now we also get convergent sums. They are the types of sums that the average person might think there is no answer to because the answer grows also to infinity!
Here is a classic example
Sn = 1+2+3+4…
Or
Sn = 2+4+8+16…
But that didn’t scare off mathematicians like Leonard Euler or Riemann. They, like true mathematicians played around with numbers and found a pattern. Their peers, especially Euler's peers criticized his results!
But now it is time to show a way to calculate divergent sums! Please note there are thousands of different ways to calculate this, but this is the most fun way for me :)

Time for the mathematics
First of we can calculate the convergent sum the following way:
Sn = 1+ ½ + ¼ + ⅛ …
We can take out a factor ½ out of the rest of the rest of the terms:
Sn = 1+ ½ (1+½+¼+...)
We see that it’s also Sn.
So:
Sn = 1+ ½ Sn
Now we get Sn alone:
Sn - ½ Sn = 1
And then we get
½ Sn = 1
Thus Sn = 2
This process works with the convergent sum, and gives us an answer that makes sense! But what about a divergent sum like one of our examples above?
Sn = 2+4+8+16…
So we can take out a factor 2:
Sn = 2+2(2+4+8+...)
Now we can write :
Sn =2 + 2Sn
Now we simplify
Sn-2Sn = 2
Now we simplify even more
-Sn = 2
Thus we get Sn = -2
Here is where I cut of this post! part two is coming tomorrow and then I will show you how we get the result for the sum of all natural numbers! Hope you are interested, leave a comment on your thoughts below! Here is a little joke!

As Always
Thanks for reading :)
If You Like what you read go and follow me Here
Once again comment, upvote an subscribe!
Thanks for reading!
