(Image Source: mathblog.dk)
If you have ever taken a math class, then you have probably seen this diagram at one point in your life:
One awful thing we sometimes do as teachers is throw mnemonic devices in the faces of students just hoping something sticks. Order of operations? Please Excuse My Dear Aunt Sallie. Trigonometric Ratios? SOHCAHTOA.
There are often really good intentions behind teaching these sayings, but sadly the concepts behind them can sometimes get lost when rote memorization is chosen as a learning strategy.
The same, I fear, is true of Pascal's Triangle.
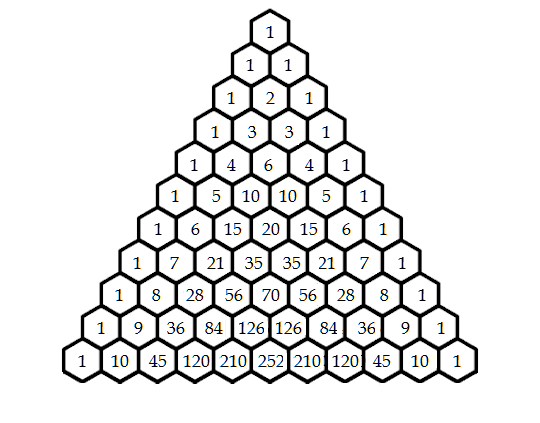
Pascal's triangle starts with the number 1 on the top. This is considered the 0th row. The next row consists of just two 1's. The row after starts and ends with a 1, but the middle number is the sum of the two numbers above. This continues so on and so forth for as many rows as are desired.
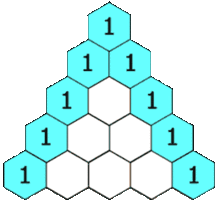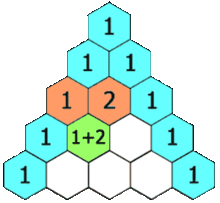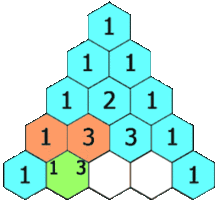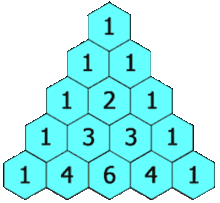
Demonstration of forming a new entry (Image Source: Wikipedia)
We teach Pascal's triangle at my school mainly to give students a way to expand binomial expressions as follows.
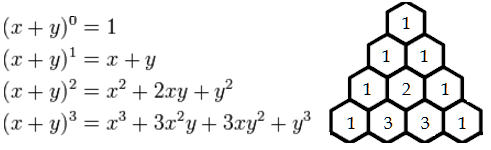
Unfortunately, that's not the really cool part about learning this triangle. That's the BORING part.
If students only knew of the multiple uses and features of Pascal's Triangle, they would run to their cell phones and tweet to the world about how cool math is. Well, in my fantasies anyways.
In reality, whenever I get to Pascal's Triangle in my curriculum, I can't contain my excitement. The more you peel back the layers, the cooler it gets!
First some brief history.

Blaise Pascal -- 1623 - 1662 (Image Source: utm.edu)
Blaise Pascal was a French mathematician, and a unique child prodigy for his time. He studied science, Christian philosophy, and was an early pioneer of automated calculators. In fact, much of his early fame derived from his work with his father, a tax collector, creating a mechanical computing device to assist with his job.

The Pascaline Mechanical Calculator (Image Source: Wikipedia)
Many of these items are known to fans of Pascal's work, but arguably his greatest claim to fame is a body of work that wasn't uniquely discovered by him. His Traité du triangle arithmétique, published in 1653 outlined a really awesome display of the Binomial Coefficients.
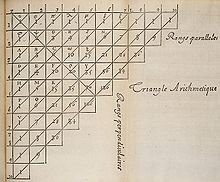
Pascal's version of "his" triangle (Image Source: Wikipedia)
We now know this pattern had probably been discovered independently by both the Persians and the Chinese during the eleventh century and studied by many other cultures centries before Pascal. However, at the time of Traité, Pascal was able to build on top of this pattern with many of the properties and applications we know to this day. And through his work, he inspired generations of mathematicians to find even more.
And those properties? Absolutely mind blowing. I've picked just a few of my face melting favorites below.
Patterns Within the Triangle
Immediately we notice some very cool patterns by looking at the diagonals of the triangle. Along the left most diagonal, we see a pattern of 1's, then the counting numbers (natural numbers), followed by the triangular number pattern.
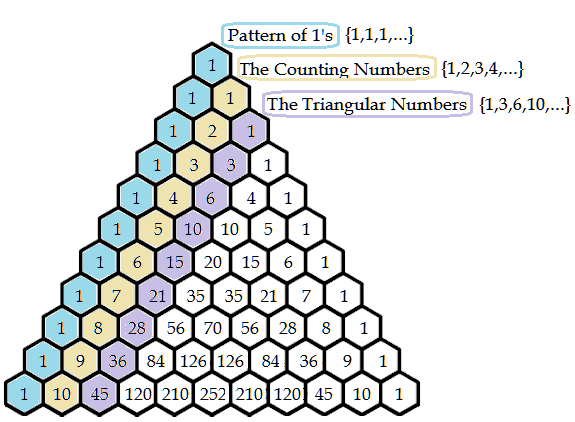
It is important to note here that triangular numbers count the objects it would take to form an equilateral triangle and are equal to the sum of the natural numbers 1 to n.

These numbers also solve the handshake problem. The nth triangular number gives us the number of handshakes that would exist in a room of n+1 individuals. Looking at the sequence {1, 3, 6, 10, 15, ...} , it is easy to determine in a room of 2 individuals, there would be 1 handshake possible, 3 individuals 3 handshakes possible, and so forth.
Why is that so awesome? Have you ever tried drawing a picture to illustrate this concept before? Here is one courtesy of NCTM that illustrates this principle for 9 individuals, or 36 possible handshakes.
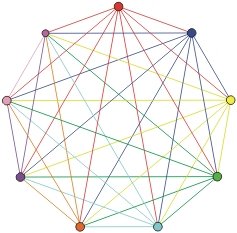
What a pain to draw!
Pascal's triangle wouldn't be convenient for say, 35 people, but that is why there is a nice formula that describes it:
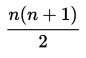
Powers of 2
Each row sum of Pascal's Triangle reveals a power of 2. I mean, how awesome is that?
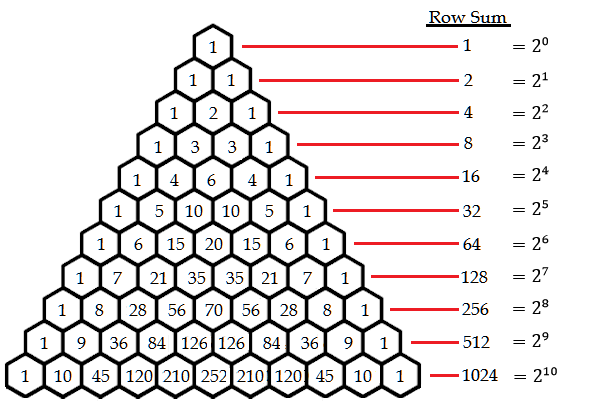
Fractals
Coloring the odd or even entries of Pascal's Triangle reveals a fractal pattern.
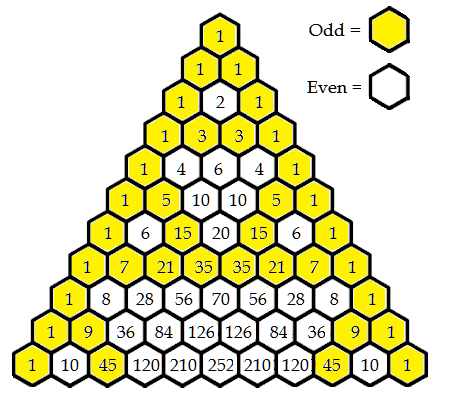
Admittedly, this doesn't look like much for my 10 row Pascal's Triangle example. However, watch what happens when you zoom out a bit:
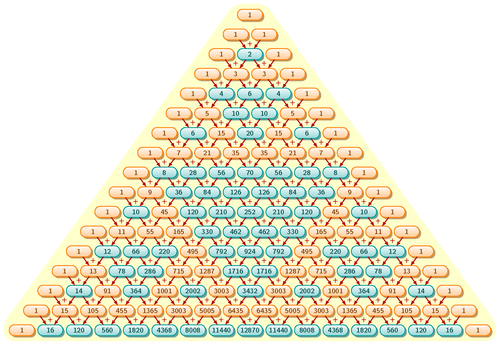
(Image Source: Math Stack Exchange)
And, even more...

(Image Source: FreeUK)
This particular type of fractal pattern is known as the Sierpenski Triangle, and is very well regarded in the mathematical community for its pure awesomeness.
Fibonacci Sequence
You know, THE famous one. The one that reveals the golden ratio?
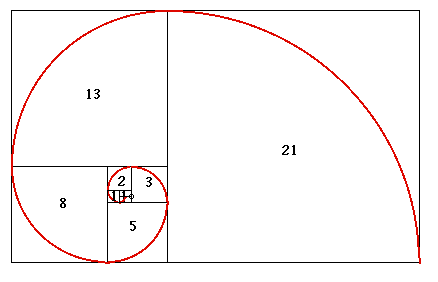
(Image Source: Univ. Georgia)
Oh yeah, its embedded in Pascal's Triangle too:

(Image Source: Wikipedia)
These lines above represent the staggered diagonals of Pascal's Triangles accompanied by their sums. Simply amazing they turn out to represent the Fibonnaci sequence!
Combinatorics
Say I have identified six Steemit users I would like to spam message to beg for upvotes. To avoid my reputation being completely nuked, I would like to choose just two of those users. How many combinations of spam messages could I send?
Well, we can count this, of course. If order is not important, and say we wanted to spam message any combination of two of the following six Steemit accounts, we would have 15 possibilities.

Now, there is a formula for this, a formula that gets pretty heavy if you aren't familiar with factorial notation (n!):
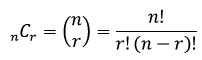
A factorial is defined for whole numbers as a number, multiplied by each whole number that precedes it, down to 1. As an example, 5! = 5*4*3*2*1. A special case is 0!=1. More on that in a moment.
But for now consider this. Every possible combination of r objects you can choose out of n is already embedded in Pascal's Triangle:

(Image Source: Live Science)
So, for our spamming example for combinations of 2 we can choose out of 6, our answer is revealed by examining the 2nd entry in row 6.
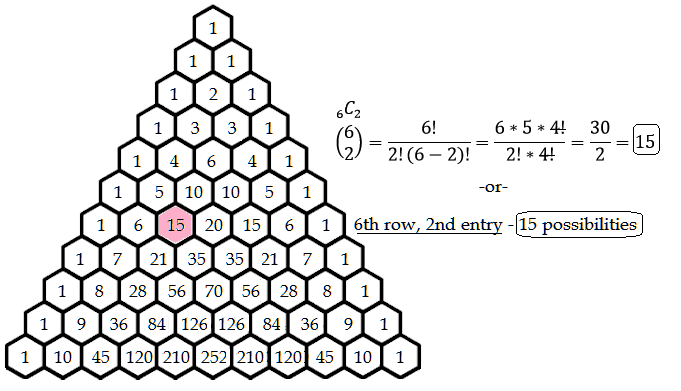
The reason why 15 is considered the 2nd entry is because the first entry in every row is considered the 0th item. Think of it like this: How many ways could I choose 0 users out of 6 to spam message?
There is exactly one way, and that is to spam message nobody. And coincidentally, that is EXACTLY the one way you probably should be considering your messages on Steemit.
This is also the reason why 0!=1. The only way we can combine zero objects is one. And that is to have zero objects.
Plinko!
If you have ever watched the Price Is Right game show, you have seen this game played before.
But, did you know Pascal's Triangle is itself a Plinko! Board? It's not exactly designed the same, but has the same idea. If you drop an object at the top of a pegboard that is modeled after the position of elements in Pascal's Triangle, you see this amazing effect:
The balls going down all stream randomly, yet at the end model a normal "bell curve" distribution!

As you can see, there is much more to Pascal's triangle than at first meets the eye. Just goes to show that much like life, there exist multiple worlds of possibilities if you just open yourself up to examining them.


