In the previous posts you learned velocity, acceleration, force and momentum. Now you will learn the basics of those in two dimensions and how to use them together Part one | Part two

( source)
The kinimatic equations mix knowledge from before together
For example, imagine an object launched at 10 meters a second and is slowing down by 1 meter a second because of air resistance. How do I figure that out? Well you could find the distance it would travel and then find the distance it would have traveled if the deceleration were acceleration and subtract them. But that isn't as easy or efficient.
We have four equations to learn today.
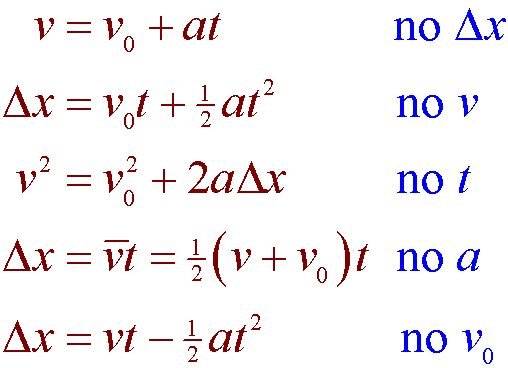
( source )
(The small subscript o next to it means original and the triangle (known as delta) means change in)
The first one you should already know from my previous posts, original velocity plus time multiplied by acceleration is the new velocity. Let's look at the units:
m/s = m/s + s * m/s^2
You can see the units match up, which is an important thing to remember. If the units do not match up you are most likely doing something wrong. Let's look at an example with numbers.
An object is going 5 meters a second when an object accelerates it by 3 meters a second for two seconds.
V = V(o) + s m/s^2
V = 5 m /s + 2s * 3 m/s^2
V = 11 m/s
Let's look at the next one
Delta x = v(o)t + 1/2 a t^2
This might be a little harder to understand at first but it is actually simple. The first part or v(o) *t is simply velocity times time like you knew before. The other part or 1/2 a t^2 (half of acceleration times seconds squared) is simple as well, the object accelerates a certain amount (the change in velocity) and half of that amount is the average. This means the change in position is equal to time multiplied by the average change in velocity plus the current velocity, see that is simple!
Let's look at the units:
m = m/s * s + m/s^2 * s^2 * (1/2)
The units match up!
Now let's try this with real numbers.
Imagine an object going 5 meters a second is accelerating by 2 meters a second squared for 10 seconds. How far has it gone?
Well using this equation we can write.
X = 5 m/s * 10 s + 2 m/s^2 *10^2 s * 1/2
X = 50 m + 100 m
X = 150m
V^2 = V^2(o) + 2a(delta)x
This one is a little more complex than the last. I will give you a conceptual understanding of it. (Because that is all I have of this one lmao)
Imagine an object falling, as it falls it gains speed. This means that the change in velocity happens over more and more distance.
An object already in motion will have less time to accelerate over the same distance. This answer can be achieved without time because of the relation between distance velocity and acceleration.
You can see better how this equation goes together by looking at the units:
(m/s) ^2 = (m/s)^2 + m/s^2 * m * 2
m2/s2 = m2/s2 + (2)m2/s2
The units match up.
Now let's try it with real numbers.
Imagine an object falling starting at 5 meters a second, now gravity is effecting it. (Gravity is 9.81 meters a second squared, usually shortened to 10 in examples.) The ground is 40 meters away, how fast is it going when it hits?
Well,
v^2 = v^2(o) + 2a(delta)x
v^2 = 25 + 20 * 40
v^2 = 825
v = 29 m/s (about)
v = 1/2(v(o) +v) * t
The next one is easy, it is simply the average velocity of an object multiplied by time.
We don't need to go over this one again.
x = vt - 1/2 (a * t^2)
The next one takes a little thinking. This one is the opposite of the second one we covered. This one is time multiplied by the velocity at the end minus the average velocity.
For example:
m = m/s * s - 1/2 m/s^2 * s^2
m = m - m
the units match up.
Imagine an object in free fall accelerating at 10 m/s^2, falling for 3 seconds and hitting the ground at 30 m/s.
x = v *t - (1/2) *a * t^2
x = 30 * 3 - (1/2) * 5 * 9
x = 90 - (45/2)
x = 68 m

( source)
Two dimensional motion
Two dimensional motion is a lot like one dimensional motion, you just need sine and cosine. Sine and cosine are used in the unit circle to find the height or width at a certain point depending on the angle given.
The secret of two dimensional motion is to split it down to one dimensional
Imagine an object going at a 45 degree angle up at 10 meters a second, how are we going to measure the change in it's velocity due to gravity?
Well you split it into two parts, cosine velocity which is x or sine velocity which is y.
Sin(45)10 = 5.3 m/s
cos(45)10 = 5.3 m/s
Now you can see it is going 5.3 m/s to the right and 5.3 m/s up. The only thing that will link them is time. In this situation it will keep going to the right at the same speed while up decelerates then accelerates. When it hits the ground both of them will (usually) stop.
How can we tell how long something is in the air for?
Well this one is not obvious at first. You split it in half, the top of the arc is where you know the velocity acceleration and beginning speed.
Which means we can use v = v(o) + at
0 = 5.3 m/s + 10 m/s^2 t
5.3 = 10 t
0.53 s = t
That is only half of the arc. The second half is the same height, so it should be the opposite on the other way. That means we can just multiply it by two to get the full time. That would mean it is in the air for 1.06 seconds. That means we can find out how far it goes.
x = v t
x = 1.06 * 5.3
x = 5.6 m
That means if you threw an object at a 45 degree angle at 10 meters a second it would only go 5.6 meters to the right. (assuming it came from the ground). If you wanted to do it from the air it would be the same thing, you would just have to calculate the arc twice and add them together.
You can also do things by adding them together
What if I want to find the momentum of an object? For example, if an object was shot at a 30 degree angle and I know how long it took to land. How about 5 seconds.
If it stayed in the air for 5 seconds and gravity is 10 meters a second how fast must it have been shot?
We can use:
v = v(o) + a * t
0 = v(o) + 10 *2.5 (2.5 seconds because we are taking the top of the arc)
v(o) = 25 m/s
It was shot up at 25 m/s.
Now how do we find the total? We have the angle which is 30 degrees. If we divide by sin(30) which would make it 50 m/s total. Now all we need is the mass of the object. We can say it is 5 kilograms, which would mean the momentum is 250 kgm/s at 30 degrees. That is not the only thing we can figure out in this situation. We can figure out how far it went to the right as well.
50 m/s * cos(30) = 43 m/s
43 m/s * 5 seconds = 215 meters
We can figure out how far it went from the time and an angle!
What about the force on an object in the launch mechanism?
Let's say it was in the tube for 2 seconds before it left.
What force did it have on the ball?
Well the ball accelerated to 50 m/s. That means it accelerated by 25 meters a second per second.
Force = mass * acceleration
f = ma
f = 5 kilograms * 25 m/s^2
f = 125 N
Plus it must act against gravity which is another 5*10 newtons of gravity. Which is 175 N total. Look at how much we can figure out about a system by just knowing a few things about it.
Units reviewed:
force =Newton = N = mkg/s^2
momentum = mkg/s
acceleration = m/s^2
velocity = m/s
position = m = meters
time = s = seconds
mass = kg = kilograms
Coming up soon
Energy and potential energy
power and energy
