Who has never heard anything about the Higgs boson, this particle that has been discovered at the Large Hadron Collider (LHC) at CERN in July 2012 and whose related theoretical works have been awarded a Nobel Prize in 2013?
I introduce below details about Higgs physics, trying to answer most questions that a non-particle physicist may have about the famous boson. While this post mainly focuses on the theory side behind the Higgs boson, the next one will address the corresponding experimental aspects.
[ Image credits: Wikipedia and CERN ]
THE STANDARD MODEL OF PARTICLE PHYSICS
In the Standard Model of particle physics, the matter sector is made of twelve particles: six quarks (up, down, strange, charm, bottom, top), three charged leptons (electron, muon, tau) and the three associated neutrinos. Each particle has then a counterpart called an antiparticle with the same properties but an opposite electric charge.
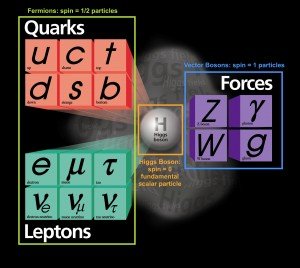[image credits: Fermilab ]
These elementary particles are interacting via the electromagnetic, the weak and the strong forces. In the quantum field theory framework, those interactions are mediated by force carriers, the so-called gauge bosons. There are several of them, namely the photon (electromagnetism), the W-boson and Z-boson (the weak interaction) and the gluons (the strong interaction).
An interaction between two elementary particles can then be seen as an exchange of a gauge boson, as illustrated in the figure below:
The ball stands for a boson and it is passed from one character to the other one. In this case, the boats will move away from each others. The interaction is said to be repulsive. Attractive interactions also exist (take two magnets for instance).
INTERACTIONS, SYMMETRIES AND THE PARTICLE MASSES
The three interactions of the Standard Model are based on symmetries called gauge symmetries. This assumption turns out to be powerful enough for deriving the properties of the force carriers and the way in which all elementary particles interact.
How can we be sure that those symmetries are the correct way to describe the microscopic world? We can never be sure, and a theory has to be tested. Data then tells us.
The Standard Model predictions have been tested in several thousands of different measurements during more than 40 years. There is up to now (almost) not a single sign of any deviation, and the gauge symmetries are suitable for explaining almost all particle physics data available today.
An example describing the Standard Model agreement with data can be found below, where the deviations between data and theory for several quantities are shown.
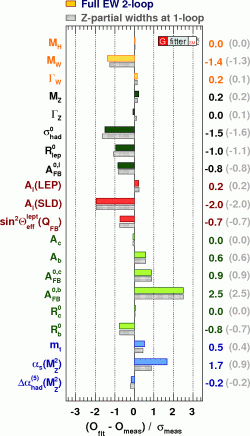[image credits: the GFitter collaboration ]
The gauge symmetries however impose that all particles are massless, which is not seen experimentally. Gauge symmetries cannot be fully wrong, as we have an amazing agreement with data. But particles are massive so that one must modify the paradigm to introduce a way to embed the particle masses within the Standard Model.
This is where spontaneous symmetry breaking rescues us. This feature is enough to give all elementary particles a mass.
SPONTANEOUS SYMMETRY BREAKING IN A NUTSHELL
What does spontaneous symmetry breaking mean?
This is explained in these three scientific publications, one being written by Francois Englert and Robert Brout, one by Peter Higgs and a third one by Gerald Guralnik, Carl Richard Hagen and Tom Kibble. The three articles are all from 1964 and they are freely available on the Internet as pieces of history.
The spontaneous symmetry breaking mechanism applied in the context of particle physics is known as the Brout-Englert-Higgs mechanism. What about Gurlanik, Hagen and Kibble? Their article came later. That is part of the tough life of a researcher: being scooped...
Spontaneous symmetry breaking can be explained with a pen:
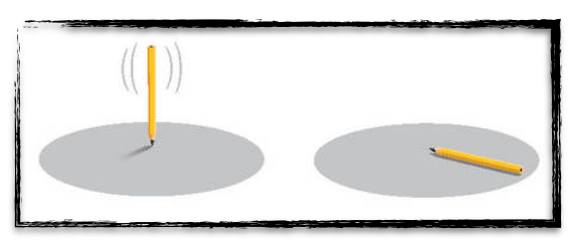[image credits: function space ]
On the left panel of the figure, the pen holds vertically (possibly because one holds it). As soon as the pen is left alone, it falls (on the right panel of the figure). The fact that the pen falls is exactly what breaks the symmetry.
To understand this last statement, we need to go back to the left picture.
There are many ways in which the pen may fall. The ensemble of all the possible ways forms the grey circle and has a revolution symmetry around the pen axis. No matter how we rotate the pen around itself, the ensemble of ways stays the same. This falling-pen problem actually features a rotation symmetry around the pen axis.
On the right panel of the figure, a specific way of falling has been adopted. The situation is not symmetric anymore. If we rotate the picture around the vertical axis (the before-fall pen axis), the fallen pen moves and we get a different figure.
A symmetry is said to be broken when the ensemble of solution (or ways in the above language) of a problem is symmetric, but one specific solution is not invariant under this symmetry.
THE RISE OF THE HIGGS BOSON
In the Standard Model, it is exactly the same situation. There are a full ensemble of viable solutions to its underlying equations, and this ensemble is gauge symmetric. Nature then chooses a specific solution to these equations and the gauge symmetries are hence spontaneously broken.
Several features consequently appear:
- All particles but the photons and the gluons get massive.
- There is a remnant of the symmetry breaking mechanism: a new particle called the Higgs boson.
- The strength of the interaction of a Higgs boson with a particle-antiparticle pair is proportional to the particle mass.
In order to validate the symmetry breaking mechanism as part of the Standard Model, once again we need to rely on data. Other options, like composite models or Higgsless theories, were considered as well before 2012.
Therefore, in order to validate the Brout-Englert-Higgs mechanism, it is necessary to first find the Higgs boson. But this is not enough. One needs also to measure its properties (in particular to validate the third item of the above list).
[image credits: the particle zoo ]