
In this first quantum mechanics lecture for 2017, I follow the teaser shown in my post on the status of fundamental physics at the end of the 19th century. I hence discuss the problematics of the atomic spectra and how they were hints for quantum mechanics at a time where it was not existing.
In a few words, classical physics at the end of the 19th century was not capable to provide a satisfactory explanation to the experimental observations related to the atomic spectra. This has consequently helped to pave the way to the development of a new theory, the quantum theory.
I will begin this post with the description of the relevant experimental status before moving on with the introduction of an empirical model explaining it, and its conceptual issues. The link between this model and the observations and the corresponding emergence of the quantum theory is left for future posts.
ABSORPTION AND EMISSION SPECTRA

[image credits: Wikipedia]
The fact that a heated gas emits visible light is well known since the 18th century. Moreover, it was also known at that time that the emitted light spectrum was composed of rays with specific wavelengths depending on the nature of the gas, or of any element in general. This is illustrated in the case of iron by the above figure.
In short, a given element was emitting electromagnetic waves at specific wavelengths once heated. This radiation spectrum is nothing but the emission spectrum of the element under consideration.
On the other hand, it was also known that white light sent through a gas was exhibiting interesting properties. The resulting light spectrum was indeed featuring dark zones, again at specific wavelengths. This is illustrated in the above picture by the black regions.
The ensemble of wavelengths associated with those darks spots in the spectrum were called the absorption spectrum of the element. Whereas white light is made of all wavelengths, some of them are absorbed by the gas and give thus rise to dark zones in the transmitted spectrum, or in other words missing wavelengths with respect to the initial spectrum.
In 1859, Gustav Kirchhoff has showed that for a given gas, the emission and absorption spectra are the same. He has concluded from there that the wavelength of those rays were characteristics of the gas. They were thus allowing one to uniquely identify the gas.
This discovery and its generalizations actually consist of the building blocks of all modern spectroscopic methods related to the identification of the chemical elements.
AN EXAMPLE: THE HYDROGEN SPECTRUM
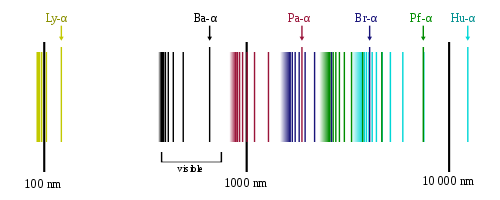
[image credits: Wikipedia]
Let us now rediscuss what we have just mentioned in the context of a specific example, hydrogen. The hydrogen (emission or absorption) spectrum is constituted of four rays in the visible domain, as observed in the middle of the 19th century by Angström (the same guy who gave his name to the unit). These are called the H-alpha (656.3 nm, red), H-beta (486.1 nm, blue-green), H-gamma (434.1 nm, blue-violet) and H-delta (410.2 nm, violet) rays and those are the four black rays shown on the above image that are in the visible domain.
This means that heated hydrogen will radiate visible light made of the four types of radiation above, with wavelengths of 656.3, 486.1, 434.1 and 410.2 nm. I recall that 1 nm equals 10-9 m.
Similarly, one can send white light (that contains all visible colors) through a cloud of hydrogen. Measuring the properties of the light transmitted by the cloud, one would notice that the transmitted spectrum exhibits four dark zones in the visible domain. Those correspond to the four above wavelengths, instead of containing components of all possible wavelengths as before going through the gas.
THE DISCOVERY OF BALMER
In 1885, Johann Balmer discovers that the four above rays do not have random wavelengths and exhibit a well-defined regular structure. He observes that the four wavelengths satisfy the relation
λn = 364.6 n2 / (n2 − 4) nm
with n = 3, 4, 5 and 6 for the alpha, beta, gamma and delta rays respectively.
Balmer then generalizes the formula and predicts new rays, in the ultraviolet regime, for larger value of the n parameter. Those rays were successfully observed later on and are shown (still in black) on the above figure.
This formula may sound a bit awkward, but it is actually at the basis of the development of quantum mechanics.

[image credits: Wikipedia]
THE REWRITING OF RYDBERG AND ITS GENERALIZATION
The formula of Balmer was rewritten in 1889 by Johannes Rydberg in terms of the inverse of the wavelength, κn = 1 / λ>n. Nothing new here, except that the above formula now reads
κn = R ( 1/22 - 1/n2 )
with R ≈ 1.0967758 × 105 cm-1 being the Rydberg constant.
The key advantage of this formula is that it can be easily generalized,
κnn' = R ( 1/n'2 - 1/n2 )
where the inverse of the wavelength κ now depends on two parameters n and n'.
We recover the rays of Balmer by setting n' to 2, but other sets of rays can been derived, with n being always taken larger than n'.
The beauty of this formula is that the ultraviolet rays predicted for n' = 1 have been observed by Lyman in 1906 and the infrared rays corresponding to n' = 3 have been observed by Paschen in 1908. Other sets of rays are correspondingly observed today, and some are shown in the hydrogen spectrum above.
In a few words, it works damned well!
[image credits: pixabay]
FROM RITZ TO BOHR: THE FIRST ATOMIC MODEL
The generalization of the Rydberg formula above exhibits a remarkable structure. It shows that the hydrogen spectrum contains rays obeying to
κnn' = Kn' - Kn
with Kn = R / n2.
But that is only the beginning of the story.
In 1908, Walther Ritz shows that the hydrogen spectrum structure is not specific to the hydrogen atom, but is valid for any atom, using an appropriate value of the Rydberg constant R. The structure of any atomic spectrum indeed obeys to
κnn' = κnn'' + κn''n'.
This has been since then experimentally verified on the spectrum of many atoms, but was revolutionary at that time.
Going back to the case of the hydrogen atom, we have now a fundamental property to explain, the fact that the radiation spectrum depends on terms of the form Kn. And at the end of the 19th century / beginning of the 20th century, this was impossible to explain with the help of classical physics only. The quantum world was needed!
Teasing my next posts, an atomic model was proposed by Niels Bohr in 1913. This model was not explainable with classical physics but allows one to obtain the value of the Rydberg constant from other fundamental constants and the form of the Kn terms. However, this model was drastically failing to explain the properties of any atomic spectrum different from hydrogen.
This is why it is known as the old quantum theory. But this is the topic of some future lesson...
SUMMARY
In this post, I have described the status of the knowledge on the atomic spectra at the end of the 19th century. I have then shown how the issue that has been one of the cornerstone leading to the development of quantum mechanics has arisen.
In my next post, I will discuss black bodies and the Planck constant, before moving on with providing many details on the Bohr model briefly mentioned at the end of this post.
I hope you enjoyed the reading of this article, and for those who have missed my previous 2017 posts, best wishes for this new year!
