Neutrinos are the less standard of the particles of the Standard Model of particle physics. I recently discussed shortly the physics behind them, and in particular, I focused on the potential of the future neutrino experiments (see here).
[image credits: Fermilab]
One of the commenters of this post kindly asked me for more detailed information, so that I decided to write down this post.
I will provide below more details on how neutrinos have been introduced, discovered, and why they can be seen as chameleons (as illustrated on the picture on the right).
In short, I will detail why neutrinos are the most intriguing of all elementary particles.
RADIOACTIVE BETA DECAYS
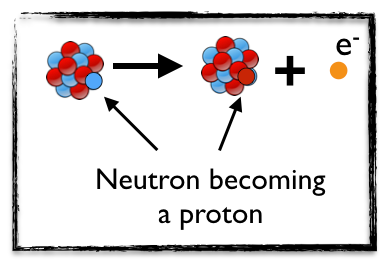
Neutrinos appeared at the beginning of the 20th century as dark particles playing a big role in radioactivity. Physicists where studying reactions where one given atomic nucleus X was transformed into another nucleus Y plus an electron (see the image below).
[image credits: homemade]
The initial nucleus X contains a bunch of protons, in red (their number being usually noted Z, that is the atomic number) and a bunch of neutrons (N), in blue.
In the reaction, one of the neutrons is converted into one proton and one electron (in orange), so that the final nucleus Y contains Z+1 protons and N-1 neutrons.
This is a radioactive beta decay, or at least how it was thought to be 100 years ago.
INTRODUCING NEUTRINOS TO SAVE ENERGY CONSERVATION
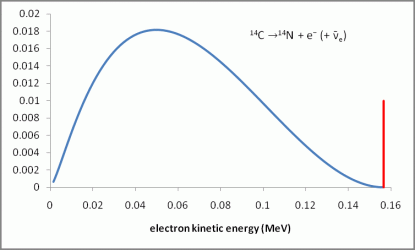
Using conservation laws, it is a very simple exercise to compute the kinetic energy of the electron (that I note Ee), that is equal to the difference between the parent and daughter nuclear masses (that I note Q).
[image credits: the T2K experiment]
This is illustrated on the picture on the right, where the kinetic energy of the electron is represented. In red, the theoretical result that simply reads Ee = Q. In blue, the observation.
The electron energy spectrum is not made of a single value, but is continuous with an end point at Ee = Q.
This was considered as an apparent violation of energy conservation at that time.
The remedy came from Pauli in the 1930ies: he proposed that there was actually a third final-state object into the game, an invisible guy that is light and that escapes any experiment undetected.
Energy conservation hence works again. It is the sum of the electron and the neutrino energies that now equals the difference between the parent and daughter nuclear masses Q. As a consequence, Ee can range from 0 to Q.
THE THEORY STRIKES BACK
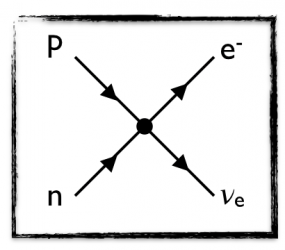
Fermi was the first to take the idea of Pauli seriously. As a reward, the dark invisible particle of Pauli has an Italian-like name, as an honor to Fermi: neutrino (noted νe).
[image credits: homemade]
Fermi modeled the reaction in which a mother neutron decays into a daughter proton, an electron and a neutrino, as illustrated by the Feynman diagram on the left.
By messing up which particle is final and which one is initial, this also dictates how neutrinos interact with matter.
The rate of the corresponding processes is extremely slow, and one can for instance calculate that a neutrino has a mean free path of thousands of light-years in water!
However, a couple of reactions per day can be obtained, if the related detectors are of the ton-scale. Although this looks crazy, this worked like a charm, and a full set of neutrino physics experiments have been successfully designed and run since then.
THREE FAMILIES OF NEUTRINOS
So far, we have connected a neutrino to an electron, but the story does not end there. Other particles resembling a lot to an electron have been found long ago: the muon and the tau. Both of these can be seen as heavier copies of the electrons.
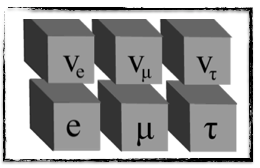
[image credits: homemade]
Similarly, other types neutrinos were discovered too, and the associated particle content is summarized in the picture on the right.
The symbols of the electron, the muon and the tau are respectively e, μ and τ, and the accompanying neutrinos are noted with the symbol ν with an index reflecting their electronic, muonic or tau flavor.
We hence have three flavor of neutrinos, which is what is included in the Standard Model of particle physics.
THE NEUTRINO MASS ISSUE
The Standard Model of particle physics is constructed on symmetries (that is its beauty after all), and those symmetries, together with data to constrain the form of the interactions, impose that neutrinos are massless.
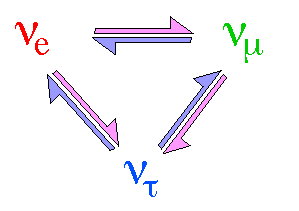
[image credits: Fermilab]
However, two decades of experiments have demonstrated that neutrinos are not that standard…
They are massive, which implies they oscillate: a neutrino of a given type can turn into a neutrino of another time when it propagates or interacts.
This is why I used this chameleon picture at the beginning of this post. We can produce an electron neutrino in one place of Earth, and detect it as a muon neutrino a few hundreds of kilometers away.
COLORFUL CHAMELEONS AND NEUTRINO OSCILLATIONS
There are various mechanisms that could explain the neutrino masses, and they all yields new phenomena that have not been observed (yet?). But there is one deep consequence, the three flavors of neutrino mix with each other.

[image credits: Fermilab]
Each neutrino can be seen as a chameleon changing its electronic, muonic or tau nature when it travels.
Let us assign colors to flavors: the electronic nature of the neutrino is red, the muonic one is blue and the tau one is yellow.
And now comes the complicated part: a neutrino actually contains each flavor in a given amount. As represented with the chameleons on the picture that are more or less red, blue and yellow.
When we observe a neutrino, we get in the detector only one of the three flavors with a probability depending on the flavor content of the neutrino (or the amount of the corresponding flavor it initially had.
This picture explains the observation very well, and current experiments are now trying to measure the physical parameters behind it with some precision.
TAKE-HOME MESSAGE AND REFERENCES
In this post, I extended the discussion on the physics of the neutrino world. I detailed how neutrinos were first introduced by Pauli to describe radioactive beta decays and then modeled by theorists. I finally come with the problematics of the neutrino masses and their oscillations.
I hope neutrino physics is now slightly clearer. Please let me know in the comments.
More information on neutrinos can be found:
- in the Particle Data Group review and there;
- in these CERN lecture notes.
For more discussion on this topic (or anything related to science), please join us on #steemSTEM. The steemSTEM project is a community-supported project aiming to increase the quality and the visibility of STEM (STEM is the acronym for Science, Technology, Engineering and Mathematics) articles on Steemit. You can also follow our curation trail on Streemian to support us.
