I bet that throughout your life you were a little surprised when your birthday coincided with the birthday of your classmate, friend or colleague.
image source
At this point you might be tempted to believe on fate, on some invisible connection, you can even start refers to this person with more sympathy. Believe me, it is not fate, but a mathematical pattern.
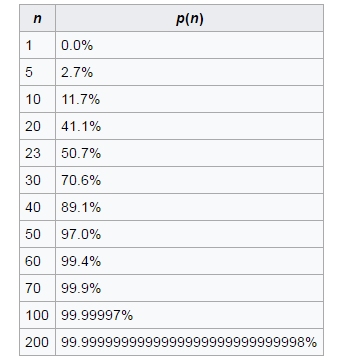
In the group of 23 three people (and more), the probability that two people will have the birthdays in same date (day and month) exceeds 50%. (less likely would be the fact that all people from this group will have a birthday on different days).
In a group of 30 people the probability of a match is already 70%, in the group of 50 people the probability is 97%.
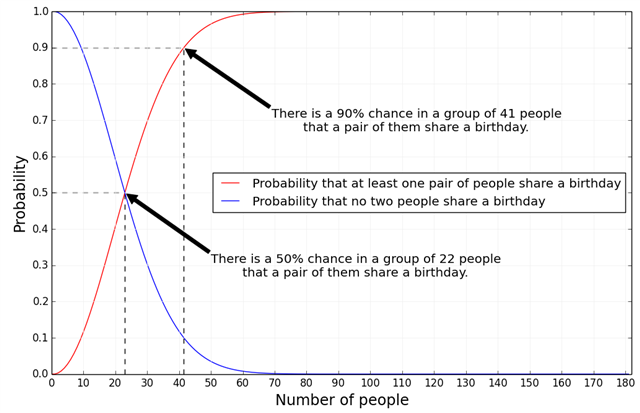
image source
The essence of the paradox is the following: Intuitively it seems that such a coincidence is unlikely, because a year of 365 days. We automatically try to count the odds, and even without precise calculations understand that they are negligible.
Our brain thinks like this:
The likelihood that one person have a birthday on a particular day is 1/365 = 0.27%. Therefore, if we have a group of 23 people, the probability of a match for all will be 0.27% * 23= 6.3%.
But, for correct solution of the task, we need to count pairs of people, not each separately. Because we are looking for a coincidence between two objects, not the involvement of each of the objects to a specific event (in this case, the date of birth).
It turns out that the number of possible pairs in a group of 23 people is 253 (vs 23 people before). In this case, the probability of a match rises significantly: 0.27% * 253= 68.31 %.
Although this is also an approximate calculation. First calculate the probability that all people in group have birthday in a different days. And then, accordingly, the probability of coincidence of two people will be the opposite value. In the end, for 23 people the probability of coincidence is 50.73% (Understanding the birthday paradox)
Logically you can guess that this probability will be 100% in a group of 366 people. (in other cases, it will tend to 100 and in fact will look like 99.999999999999999...%)
The essence of the paradox is the distinction between intuitive perception of the person and the results of mathematical calculations. Many things seem to us incredible, when in fact they obey the laws of mathematics.
