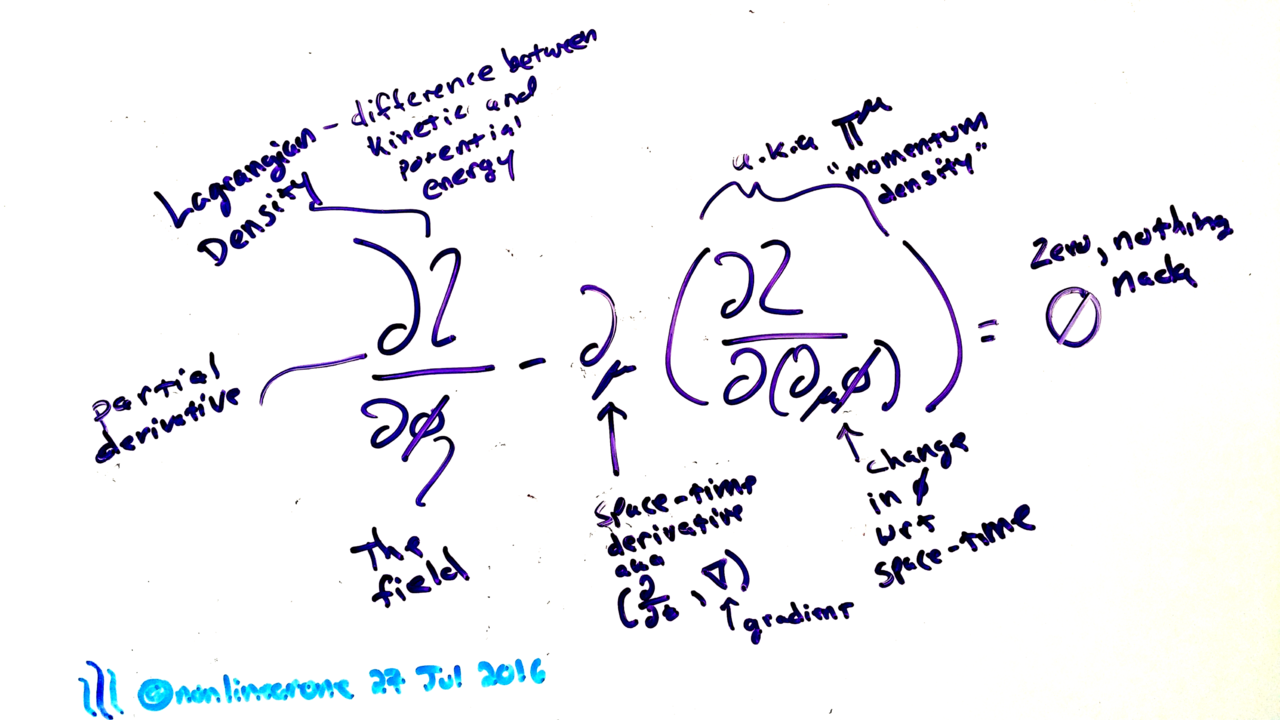
Here's an image of an equation from my whiteboard, with annotations to explain (a bit at least) what each of the symbols means. If you like it, please let me know and I can try to explain a bit more of what's going on.

The Euler-Lagrange Equation

Brief Description

In the calculus of variations, the Euler–Lagrange equation is a second-order partial differential equation whose solutions are the functions for which a given functional is stationary. [1]

Usage

Given a Lagrangian density, find the equations of motion.

Related Fields of Math and Physics

The calculus of variations [1]. Classical field theory [2]. Quantum field theory [3].

Photo Source

Me. I have a Ph.D. in physics and wrote this on my whiteboard.

References and Recommended Reading

[1] https://en.wikipedia.org/wiki/Euler%E2%80%93Lagrange_equation
[2] https://en.wikipedia.org/wiki/Classical_field_theory#Lagrangian_dynamics
[3] https://en.wikipedia.org/wiki/Quantum_field_theory#Lagrangian_formalism
[4] Quantum Field Theory for the Gifted Amateur - Lancaster & Blundell 2014 - Chapter 7 - Examples of Lagrangians or How to Write Down a Theory