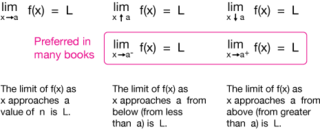Calculus is a field of mathematics that I really like to talk about! It is just amazing how many practical applications calculus have! Today I will write about differentiation, specifically a "paradox" that may occur when you think intuitively about what is differentiation!

Image Credit of original photo
What is Differentiation?
Note: I am not going to use Scientific accurate words like displacement ect. it is just basic stuff!
Well in the 1600s great mathematicians like Newton and Leibniz found a way to calculate the slope of a point, which in return helped you to calculate the slopes of curves. This meant that we can calculate more accurate position time models to find velocity ect.
But let us think about what is velocity! it is the change in distance divided by the change in time. So in simpler terms if I want to figure out how fast I drove my car without a speedometer, then I need to take the distance I drove lets say 50 km and divide it by the time it took me, lets say 30 min. so it would look something like this 50/30 = 1.67 km per minute or 100 km per hour!
But here is what calculus is doing, it says we can take multiple pictures of me driving this 50 km and calculate my speed on that picture, on that point of time!

Image Credit:
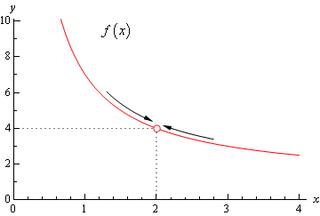
Defining velocity on a point
It is important to note that our velocity did change throughout our 50 km ride, we did not magically just started the car and instantaneously drove 100 km/h and then stopped after 50 km at 0 km/h. We had to speed up and then drive a certain speed and then slow down again! The 100 km/h that we calculated is only the average speed of the trip. So for some interval of time our speed was fast and others it was very slow!
But note that it is still some interval of time, not a point in time! To calculate velocity one needs a small change in distance and time. A point is a point, it would mean the change from Point A to Point A which is zero and the change of time is X min to X min, meaning no time has changed!
So to calculate velocity of a point, we are calculating the velocity of something that has not moved nor did any time pass as it did not move... so basically saying 0/0. We know that dividing by 0 does not exist!
This paradox however was not a problem for mathematicians, they are smart and creative. They created tools to bypass these types of problems. One of these tools is the idea of the limit.
Defining Limits
The idea of a limit is thinking: "What happens to a function's output when it goes closer and closer to certain x value". So they are actually studying the function on how close it gets to a point and not actually what happens when you throw in that value. So it allowed mathematicians to see what happens if you divide a function with a 0, since you do not actually divide by 0. This is really cool, here is an image that graphically illustrates the idea:
here is also some limit notation:
So this sound like a cheat, but with careful (and dangerous) arguments mathematicians could argue that a point is the following:
A point is the opposite of infinity, instead of finding a space that goes bigger and bigger, a point is some interval that is the smallest ever, it is not zero but is very close to zero. It is called a infinitesimal which just means very small.
so by applying the limit theory, mathematicians like Newton argued that one can study and see what the velocity would look like if the change in distance in time tends to be at size of a point!
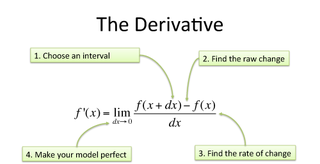
Image Credit
This is amazing because there is a change in distance and time, just a really really small one, but still there is change. In conclusion, we can safely say:
That with smart logical arguments, mathematicians can break down a paradox/problem and find a solution!
what do you think? leave a comment down below. Do not forget to upvote, Resteem and follow my blogspot!
check out more posts Here
I am back, after half a year! thanks for still following me!