En la publicación anterior presenté las nociones fundamentales de la Teoría de Conjuntos, en esta ocasión continuaré con la temática, dando inicio a las Operaciones con Conjuntos, específicamente la Inclusión y la Igualdad. En las siguientes publicaciones continuaré con el resto de forma paulatina.
Comenzando con la Inclusión de Conjuntos se puede decir que se refiere a la idea de un determinado conjunto A contenido dentro de otro conjunto B, también se puede afirmar que si A está dentro de B entonces A es subconjunto de B o A está incluido en B.
Simbólicamente, decir que un cierto conjunto A está incluido en B se denota: A⊂B, esto quiere decir que todos los elementos del primer conjunto pertenecen al segundo conjunto, de lo cual se desprende su definición:
Sin embargo, es posible que se dé un caso en el cual no todos los elementos que se encuentren en el primer conjunto se encuentren en el segundo conjunto, en este caso se dice que A no es subconjunto de B o A no está incluido en B. Simbólicamente se representa A⊄B. Más específicamente hablando, la no inclusión es posible cuando existe al menos un elemento que no verifica la definición, esto es, que existe al menos un elemento que pertenece al primer conjunto pero no se encuentra en el segundo conjunto. En símbolos:
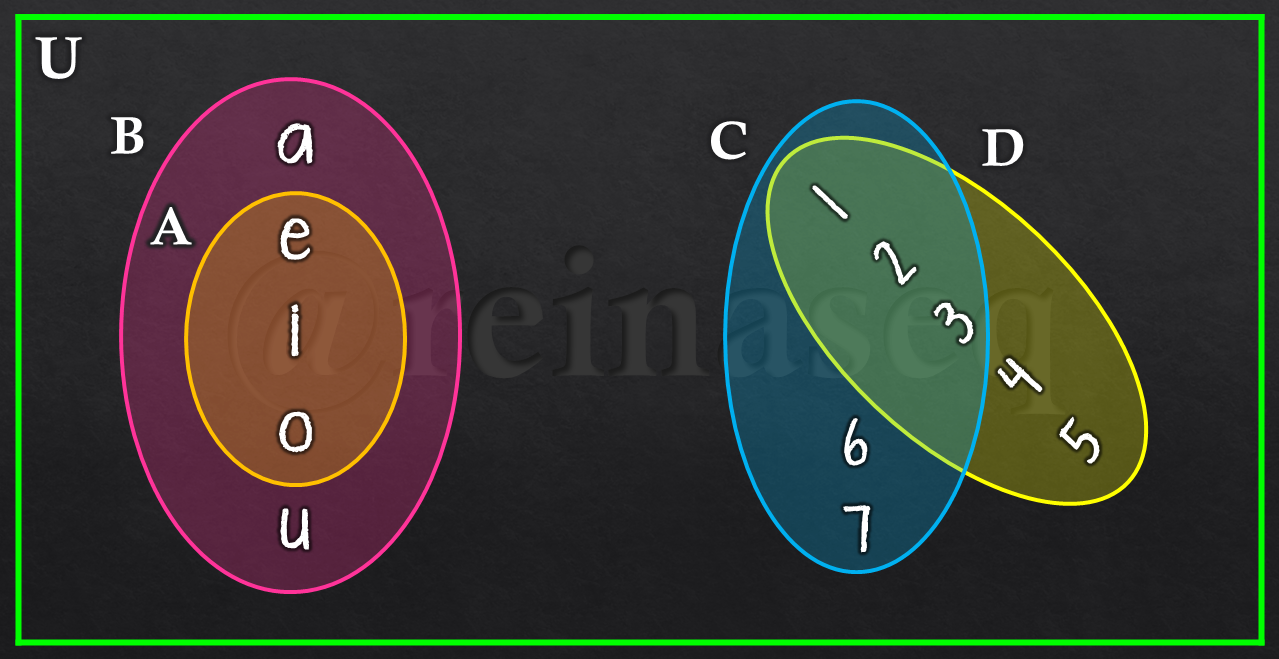
Observemos el siguiente Diagrama de Venn
Lo mostrado nos lleva a concluir en primer lugar que A⊂B en tanto que verifica la definición dada, es decir, todo elemento de A pertenece a B. Por otro lado, se puede afirmar que C⊄D, ya que a pesar de que existen elementos en común entre los dos conjuntos existe al menos un elemento que pertenece a C que no se encuentre en D.
Propiedades de la Inclusión
La Inclusión de Conjunto cumple con las siguientes propiedades:
- Reflexividad: Esto quiere decir que todo conjunto está incluido en sí mismo, dicho de otra forma, todo conjunto es subconjunto de él mismo. Esto se afirma porque A⊂A cumple con la definición de inclusión, esto se visualiza de la siguiente manera en símbolos:
- Transitividad: Para que se verifique esta propiedad deben haber al menos tres conjuntos, a saber, A, B y C y ocurrir que si el primer conjunto está incluido en el segundo y a su vez el segundo está incluido en el tercero, se concluye entonces que el primero está contenido en el tercero. En otras palabras, si el primer conjunto es subconjunto del segundo y el segundo es subconjunto del tercero, entonces el primero es subconjunto del tercero, todo esto en virtud de que se cumple con la definición de inclusión de conjuntos. En símbolos se escribe como sigue:
Entiéndase que la flecha en la expresión simbólica es una implicación, es decir, todo lo que se encuentra a la izquierda de ella se conoce en Matemática como la hipótesis y lo que está a la derecha se conoce como la tesis. Esto indica que considerando la hipótesis y la definición de inclusión se puede demostrar la tesis.
Demostración
∀x∈A⇒x∈B, por hipótesis A⊂B
⇒x∈C, por hipótesis B⊂C
⇒A⊂C, por definición de Inclusión de Conjuntos
∴Se demuestra que A⊂B ∧B⊂C⇒ A⊂C
- Antisimetría: Esta propiedad se verifica entre dos conjuntos A y B cualesquiera si ocurre que los elementos del primer conjunto pertenezcan al segundo y los elementos del segundo pertenecen al primero entonces se concluye que tales conjuntos son iguales. La afirmación se representa en símbolos como sigue
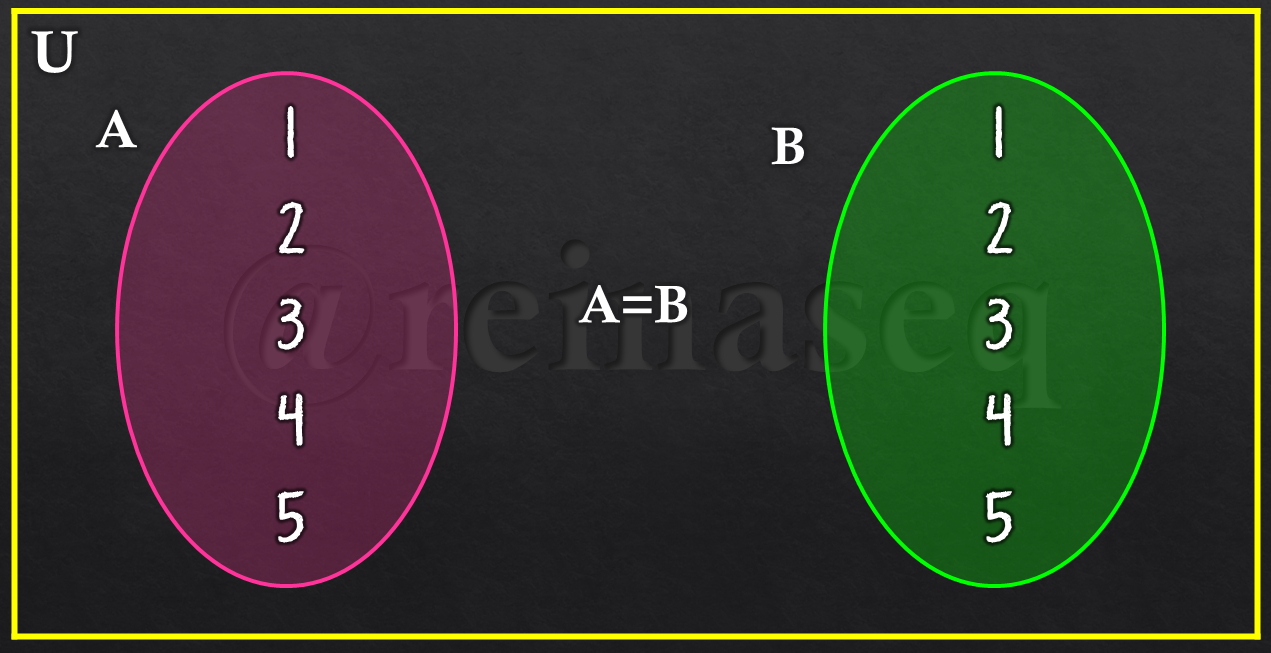
Igualdad de Conjuntos
Cuando pensamos en la posibilidad de que dos o más conjuntos sean iguales, lo primero que podemos responder es lo obvio, deben tener los mismos elementos. Matemáticamente hablando y teniendo presente la definición de Inclusión de Conjuntos, se dice que dos conjuntos cualesquiera A y B son iguales si y sólo si los elementos del primer conjunto pertenecen al segundo y los elementos del segundo pertenecen al primero. Esto quiere decir que para demostrar que dos conjuntos son iguales se debe a su vez demostrar la doble inclusión. En símbolos, esta definición se representa como sigue
Puede ocurrir que alguna de las dos inclusiones no se cumpla, en ese caso se afirma que no se cumple la definición de Igualdad de Conjuntos o dicho de otra forma los conjuntos son diferentes. Tal afirmación se expresa de la siguiente forma
Ejemplo: Dados los conjuntos A y B definidos como sigue
A={x∈R/x^2=x} (x^2 es el cuadrado de x)
B={x∈R/(x-1).x=0}, demostrar que A=B
Demostración
Como ya se ha indicado, demostrar una igualdad de conjuntos pasa por demostrar la doble inclusión A⊂B ∧B⊂A, eso quiere decir que se puede proceder demostrar cada inclusión por separado y al hacerlo concluir con la igualdad de conjuntos. Aparte de las definiciones de Inclusión e Igualdad de Conjuntos, se deben tomar en cuenta las definiciones que se dan para A y B en el encabezado del problema y a su vez las propiedades del conjunto numérico en el cual están definidos. Como se puede observar, tanto A como B son subconjuntos del Conjunto de los Números Reales R, por tanto las propiedades que se cumplen en él para las diferentes operaciones son utilizables en la demostración solicitada. Por otro lado, se debe observar que la doble inclusión están expresadas por una Conjunción (∧) lo cual indica que deben cumplirse las dos de forma simultanea para concluir con la Igualdad de Conjuntos. En caso de que alguna de ella no se verifique entonces se concluye que los conjuntos dados son diferentes, es decir, no se cumple con la definición de igualdad. Procedamos:
i ¿ A⊂B?
∀x∈A⇒x^2=x , por definición del conjunto A
⇒x^2+(-x)=x+(-x) , sumando (-x) a derecha en ambos miembros de la igualdad
⇒x^2+(-x)=0 , por definición de elemento opuesto en R
⇒x.x+(-x)=0 , propiedad de Potenciación en R
⇒x.(x-1)=0 , propiedad distributiva en R
⇒(x-1).x=0 , propiedad conmutativa de la multiplicación en R
⇒x∈B, por definición del conjunto B
∴Se demuestra que A⊂B , por definición de Inclusión de Conjuntos.
ii ¿ B⊂A?
∀x∈B⇒(x-1).x=0 , por definición del conjunto B
⇒x.(x-1)=0 , propiedad conmutativa de la multiplicación en R
⇒x.x+(-x)=0 , propiedad distributiva en R
⇒x^2+(-x)=0 , propiedad de Potenciación en R
⇒x^2+(-x)=x+(-x), por definición de elemento opuesto en R
⇒x^2+[(-x)+x]=x+[(-x)+x], sumando x a derecha en ambos miembros de la igualdad
⇒x^2+0=x+0, por definición de elemento opuesto en R
⇒x^2=x, por definición de elemento neutro para la adición en R
⇒x∈A, por definición del conjunto A
∴Se demuestra que B⊂A , por definición de Inclusión de Conjuntos.
∴ Por i y ii se demuestra que A=B, por definición de Igualdad de Conjuntos
En las siguientes publicaciones seguiré con la temática de Operaciones con Conjuntos, desarrollando otra en particular.

Las matemáticas expresan valores que reflejan el cosmos, incluyendo el orden, equilibrio, armonía, lógica y belleza abstracta - Deepak Chopra .

Referencia
Armando, R. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Todas las imágenes, separadores y banners de este artículo son de autoría propia.
Artículo Anterior