English (deutsche Übersetzung unten)
Advantages and disadvantages of a linear reward curve compared to n^2.
The question which of the reward curves is better, n^2 or a linear one of the most discussed here on Steemit. Just recently @dan emphasized again, that he clearly is in favor of a non-linear curve, while @ned commented to be convinced of the opposite.
Actually both curves are having advantages and disadvantages:
- Because of its flat beginning n^2 discourages self-votes on articles and especially also comments on which nobody else is (or only very few are) voting. However the disadvantage is, that it leads to extreme rewards for posts which receive a big amount of upvotes.
- A linear reward curve doesn't have the disadvantage of n^2. However upvoting own comments (or articles with few other upvotes) is now much more attractive than before.
Would a sigmoid reward curve be a suitable solution?
One try to solve both problems with one single function would be to use a sigmoid reward curve. Due to it's flat begin it would be far less attractive to upvote posts on which nobody else is voting (self-voting of comments would be less attractive). As it also ends flat, extreme rewards (other than with n^2) would be avoided, as well.
It was @twinner who mentioned this idea, and I still think it would be an interesting solution. One problem could be that graphs of sigmoid functions are approaching a limiting value so that finally further upvotes nearly wouldn't have any effect anymore.
What about 'conciliating' (combining) both curves?
Thinking about all that I got a new idea. Before presenting it let me emphasize that ideas are there to be either further developed if others find them to be interesting, too, or to be discarded in case they are just unfeasible. I am well aware that my idea may have some flaws I am not yet aware of or may be just too complicated to implement (which I doubt).
So what about if the reward curve started as y = n2 with a flat beginning (against self-votes) and a steep slope afterwards? Then, after "n" had exceeded a certain value, the curve could become linear (y = m·x + b; where for example m = 1 and b gets allocated exactly that value that the next y-value will be one unit higher than the previous y-value, so that there is no interruption of the incline of the curve). The advantage of the linear ending would be to avoid extreme rewards (like n^2 causes) but at the same time having no limiting value like a sigmoid function.
Such a curve could look like this (that's just an example, it's the idea which matters - I am just an ordinary Steemit-user giving the implementation into the hands of professionals who are getting paid for doing things like that. :-)))
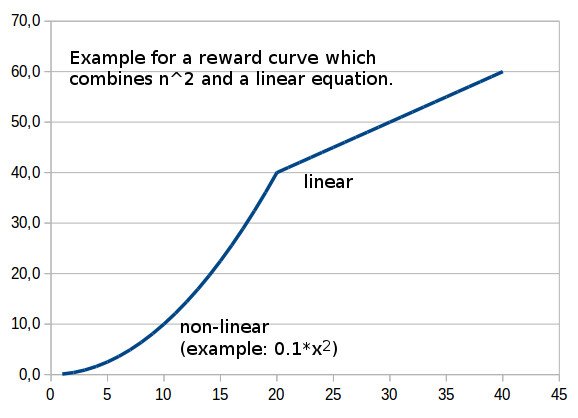
Deutsch
Vor- und Nachteile der linearen Reward-Kurve verglichen mit n^2.
Die Frage, welche der beiden Reward-Kurven, n^2 oder linear, die bessere sei, ist eine der meist diskutierten hier auf Steemit. Gerade erst kürzlich betonte @dan erneut, dass er ganz klar eine nichtlineare Kurve bevorzugt, während @ned kommentierte, vom Gegenteil überzeugt zu sein.
Letztlich sind mit der Implementierung beider Kurven sowohl Vor- als auch Nachteile verbunden:
- Aufgrund ihres flachen Beginns ist n^2 ein gutes Mittel gegen Selbsvotes von Artikeln und besonders auch Kommentaren, die bis dahin von niemand anderem (oder nur sehr wenigen) upgevoted wurden. Allerdings besteht der Nachteil darin, dass es im Falle sehr zahlreicher Upvotes zu extremen Rewards per Post kommen kann.
- Eine lineare Kurve weist diesen Nachteil von n^2 nicht auf. Allerdings begünstigt sie das Upvoten eigener Kommentare (oder Artikel mit wenigen anderen Upvotes).
Wäre eine sigmoide Reward-Kurve eine sinnvolle Lösung des Problems?
Einen Versuch, beide Probleme mit einer einzigen Funktion zu lösen, stellte die Nutzung einer sigmoiden Reward-Kurve dar. Ihres flachen Beginns wegen wäre es viel unprofitabler, Posts upzuvoten, die ansonsten keine anderen Upvotes erhielten (eigene Kommentare zu voten wäre weniger attraktiv). Da sie außerdem auch flach endet, würden extreme Rewards (anders als bei n^2) ebenfalls vermieden.
Es war @twinner, der diese Idee erwähnte, und ich halte sie immer noch für eine interessante Lösung. Ein Problem dabei könnte sein, dass sich die Graphen von Sigmoidfunktionen einem Grenzwert annähren, so dass schließlich weitere Upvotes fast keinen Effekt mehr hätten.
Wie wäre es damit, beide Kurven miteinander zu 'versöhnen' (sie zu kombinieren)?
Während ich über all das nachdachte, kam mir eine neue Idee. Bevor ich sie euch vorstelle, möchte ich betonen, dass Ideen dazu da sind, weiterentwickelt zu werden, wenn andere sie ebenfalls interessant finden oder verworfen zu werden, falls sie sich als undurchführbar erweisen. Mir ist bewusst, dass meine Idee möglicherweise Schwachstellen hat, die ich nicht berücksichtigt habe oder vielleicht zu kompliziert zu implementieren ist (was ich eher nicht vermute).
Also, wie wäre es damit, die Reward-Kurve als y = n2 mit flachem Beginn (gegen Selbstvotes) starten und danach steil ansteigen zu lassen? Dann, nachdem "n" einen bestimmten Wert überschritten hat, könnte sie in eine lineare Funktion übergehen, z. B. y = m·x + b; wobei zum Beispiel m = 1 sein könnte, und b genau den Wert zugewiesen bekäme, dass der folgende Y-Wert eine Einheit höher wär als der vorherige Y-Wert, so dass der Anstieg der Kurve nicht unterbrochen wäre). Der Vorteil des linearen Endes der Kurve wäre es, extrem hohe Profite (wie sie n^2 verursacht) zu verhindern, aber zugleich keinem Grenzwert zuzustreben wie eine sigmoide Funktion.
Solch eine Kurve ist oben abgebildet. (Es handelt sich dabei nur um ein Beispiel - es ist die Idee, um die es mir geht; ich bin nur ein gewöhnlicher Steemit-Nutzer, der die Implementierung gerne den Experten überlässt, welche dafür bezahlt werden, so etwas zu tun. :-)))
