The integral of 1/√e2x+1 looks like a challenging problem. And it is, but it's not as bad as you would think. And as usual, there are multiple ways of tackling it.
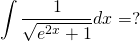
As I've stated, when it comes to the world of real functions, there really are only 2 methods of integration:
- Integration by substitution
- Integration by parts.
Let's have a go with integration by substitution. To do this, we let...
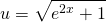
And thus by rearranging, we can express e2x as...
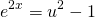
And now, differentiating both sides with respect to x...
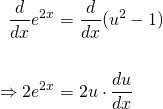
...and cancelling the 2's on both sides, then rearranging to isolate the dx term on the left-hand side...
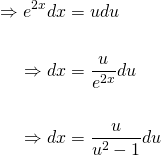
Alright. Now, that we have all of our bits and pieces, let's make our substitution!
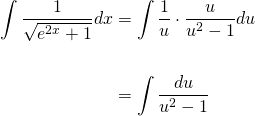
Now, the integral of 1/u2-1 can either be treated as an inverse hyperbolic problem, or a partial fractions problem. The latter is a less advanced, so let's go with that for now.
The fraction 1/u2-1 can be expressed as...
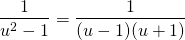
...and breaking this up into its partial fractions...
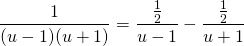
So the integral becomes...
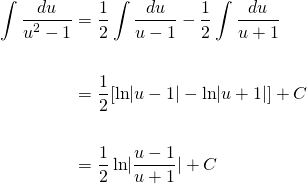
Cool, we're almost done. Let's now back substitute our expression for u to complete the integration...
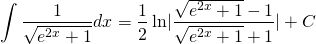
And that's it folks!
Please give me an Upvote and Resteem if you have found this tutorial helpful.
Please ask me a math question by commenting below and I will try to help you in future tutorials.
I would really appreciate any small donation which will help me to help more math students of the world.
Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu
