This article introduces what I call the "crossing the bridge" short-cut. Here is an example of an algebraic equation solved using the standard orthodox methods.
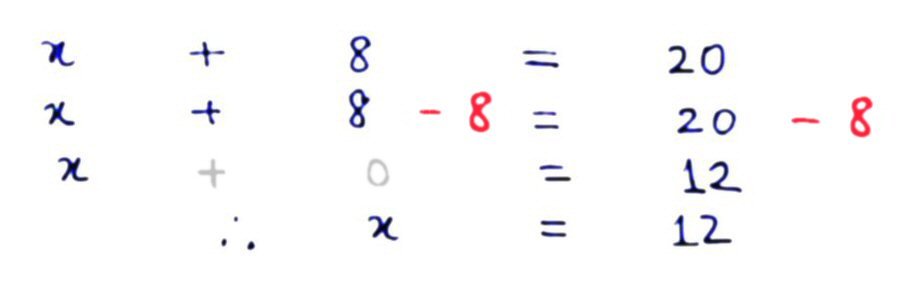
To "get rid" of the 8 on the LHS, we subtract both sides of the equation by 8. This is legit. Even though we do not know what 'x' is, we know that x is a real number, so it obeys the same laws of arithmetic as other numbers. When we do the same thing to equal quantities, we still get quantities that are equal to each other (although they may or may not be equal to the original quantities). On the RHS, 20 - 8 simplifies to 12, and we get a + 8 and a - 8 on the LHS, which is the same as 0. And of course x + 0 is the same as x. The 'unknown' quantity x is now known to be 12.
If you observe the above working, you realise that the effect of subtracting - 8 on both sides makes it 'as if' 8 on the left becomes - 8 after crossing over the = sign. I call this 'crossing the bridge'. We get a simplified working.
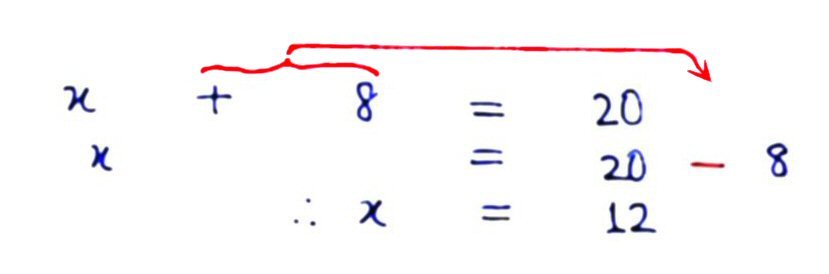
Here is another example of Crossing the Bridge. This time, - 8 on the LHS crosses over and changes to + 8. Of course it is important to understand the basic principle of adding and subtracting equal quantities to hoth sides of the equation. Once you understand that, then you can apply this short cut, because you know that it is based on legitimate operations.
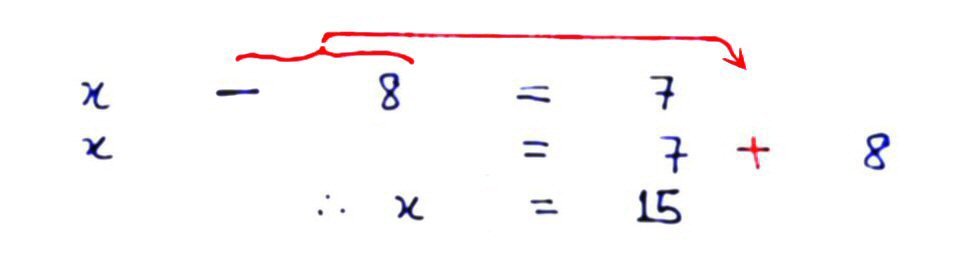
Here is a more involved example.
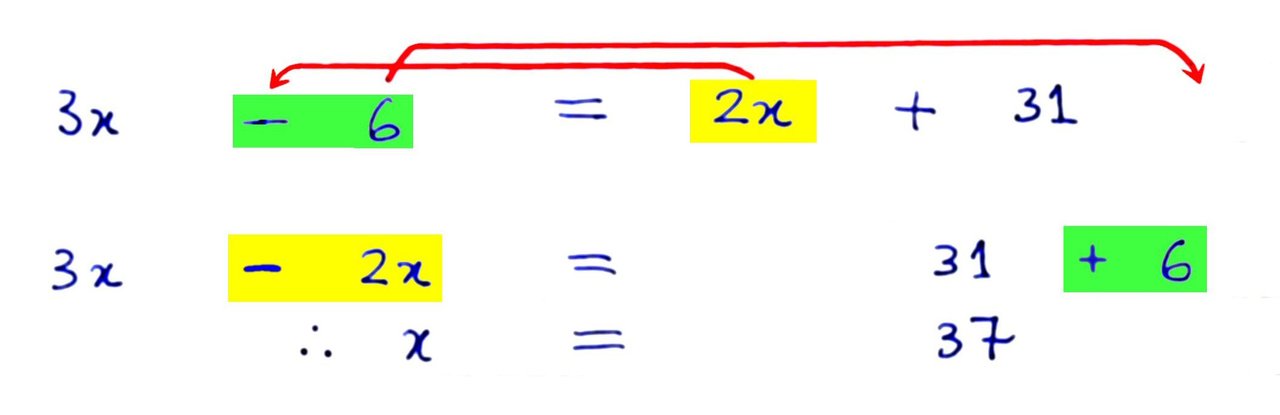
Here, -6 crosses the bridge from the left and becomes + 6 on the right. At the same time, 2x on the right crosses over to the left and becomes - 2x.
Note that "Crossing the Bridge" involves + and -, whereas "The Escalator" is for multiplication and division. When "Crossing the Bridge", you go straight across, not over or under, but change the + or - sign.
Finally, we have one example that combines "Crossing the Bridge" with "The Escalator".

First, 7 on the LHS crosses over to become -7 on the RHS, while -6x on the RHS crosses over to become 6x on the LHS. After simplifying, we get 2x = 12. Remember that x wants to be alone. So 2 has to move. Since 2 is connected with x by multiplication (not by + or -), we use the Escalator to move 2 down across to the right hand side. We have 12/2 which simplifies to 6. So finally we found our axe. Or is it your ex? Do you have an axe to grind with your ex?
Anyway, I hope you have learned something useful!
