I have introduced Mr Sandman and Mr Upside-Down in an earlier article.
In this article, I shall illustrate integer arithmetic with more examples. Remember that what our Sandman calls a “hole” is a “mound” to Mr Upside-Down.
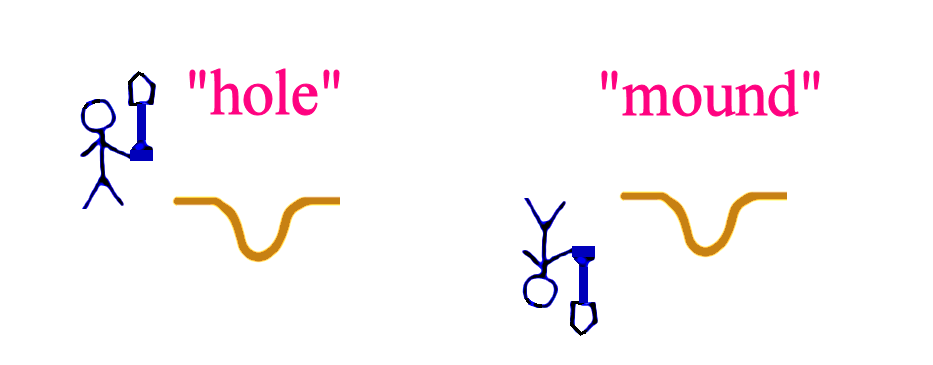
Whenever we have a whole (i.e. mound) and a hole, they cancel in the sense that we can use the sand from the mound to fill up the hole and we get level ground (i.e. 0).
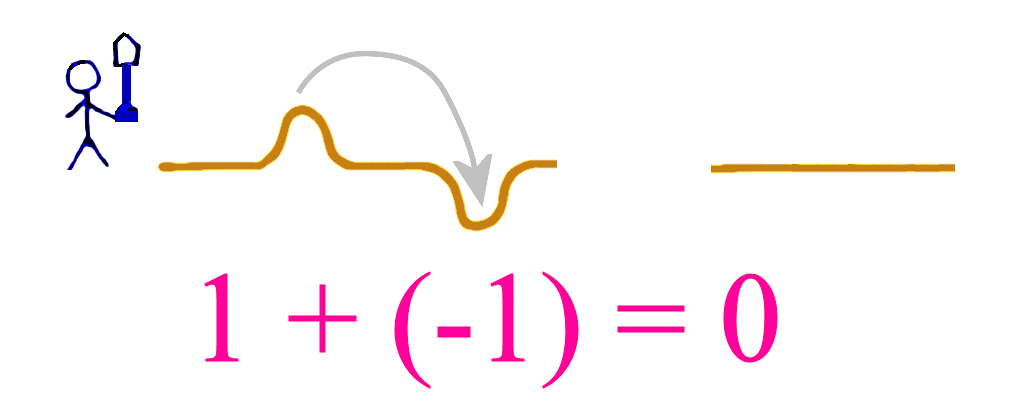
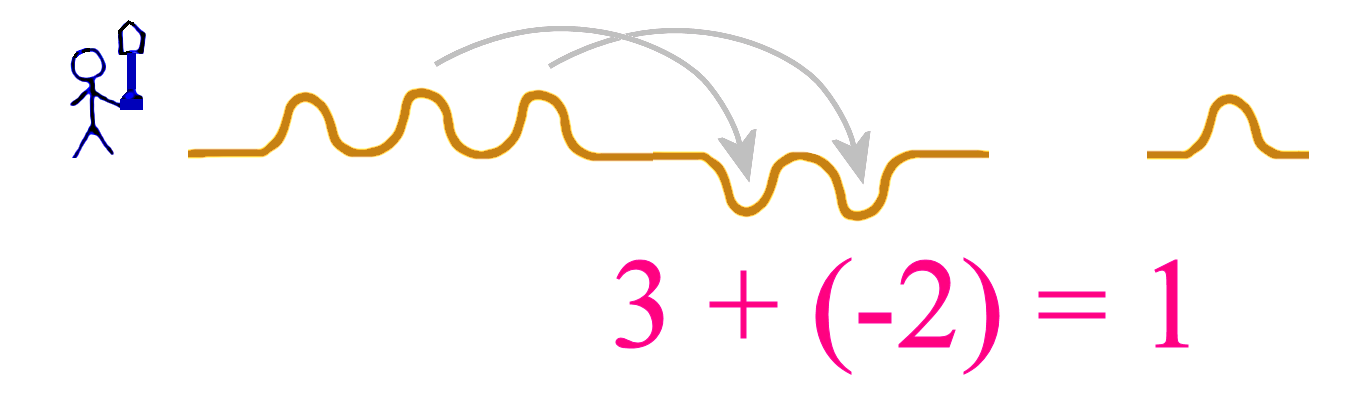
If we have 3 mounds and we add 2 holes, then we use two of the mounds and fill up the holes, and we are left with 1 mound.
You will notice that this is the same result as if we had 3 mounds and then we removed 2 of the mounds. 1 mound remains.
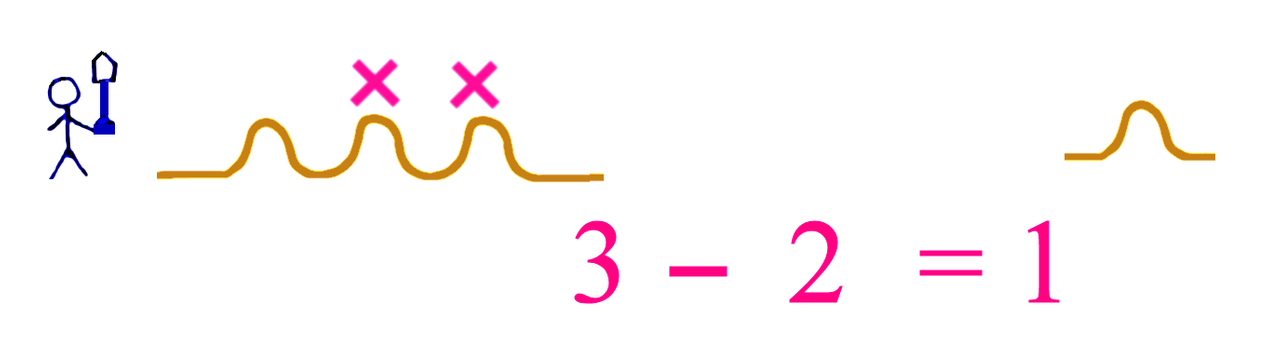
If we start with one hole (-1) and we get Mr Sandman to dig (– ) two holes, then we get 3 holes, so -3.
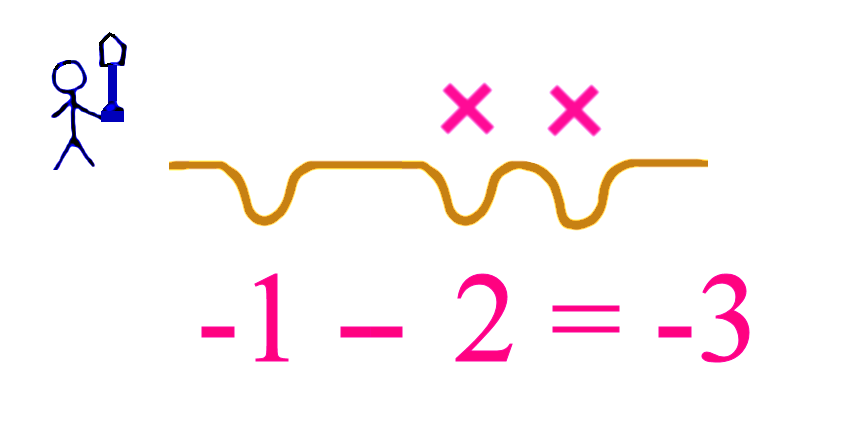
But if we start with one hole (-1) and we get Mr Upside-Down to dig (– ) two of his “holes” (so he is subtracting -2), then we actually get two real mounds. So this is really like adding 2. After levelling our original hole with one of the mounds, we are left with 1 mound. So -1 – (-2) = -1 + 2 = 1.
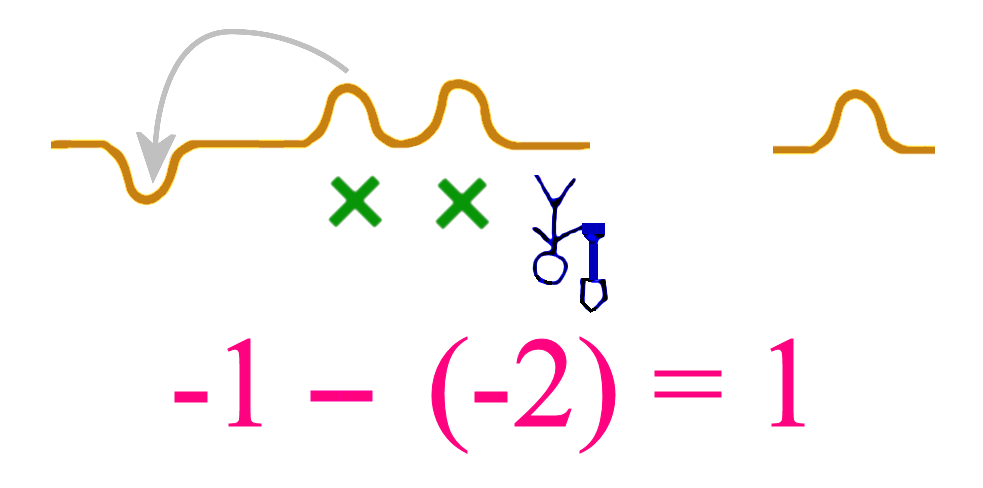
I hope you have enjoyed my presentation and learned something.
