There has been an on-going controversy raging on in cyberspace concerning a seemingly straight-forward arithmetic problem of multiplication by repeated addition. In Singapore, this idea would be taught as early as grade 2, or grade 1 even. I wanted to write my opinion on that matter, but first I think we need to settle some fundamental concepts, so that we are on the same page.
Mathematics is a subject that has developed over more than 2000 years. Controversies and debates in mathematics are nothing new, and these actually helped to clarify our concepts and put them on a rigorous footing. Modern mathematics is built on set theory, which was invented by Georg Cantor. His clarified the meaning of “number”, even going into infinite numbers. In this article, we shall restrict our discussion to finite numbers.
So what is a number? And what does it mean to “count”? If we have a set of distinct objects and we do a one-to-one substitution of objects (this is called a “bijection”), the “number of elements” or “cardinality” remains the same. We can define number as that property which remains unchanged through one-to-one correspondences. Counting is the process by which we associate objects of a set with the numbers 1, 2, 3, ... etc.
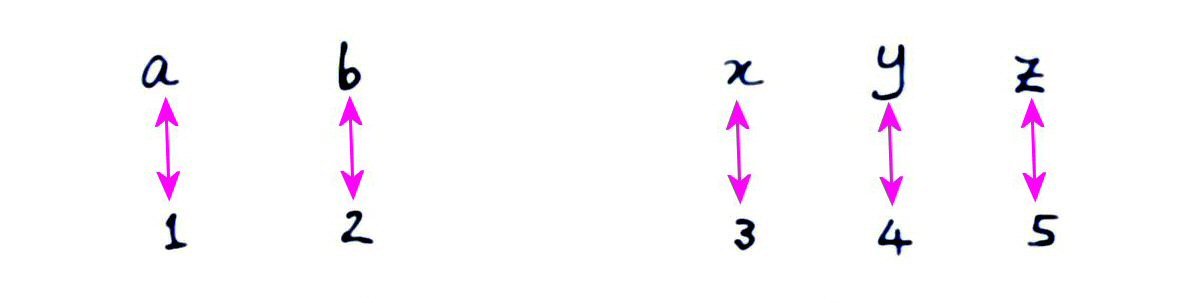
What does it mean to add? To add means to enumerate or count the elements of a disjoint union of sets. “Disjoint” means that the sets have no elements in common. There are no overlaps or repeats. In our example below, {a, b} and {x, y, z} are disjoint sets, and the number of elements #({a, b}) = 2 and #({x, y, z}) = 3. Their union is the set {a, b, x, y, z} whose number of elements is 2 + 3 = 5.
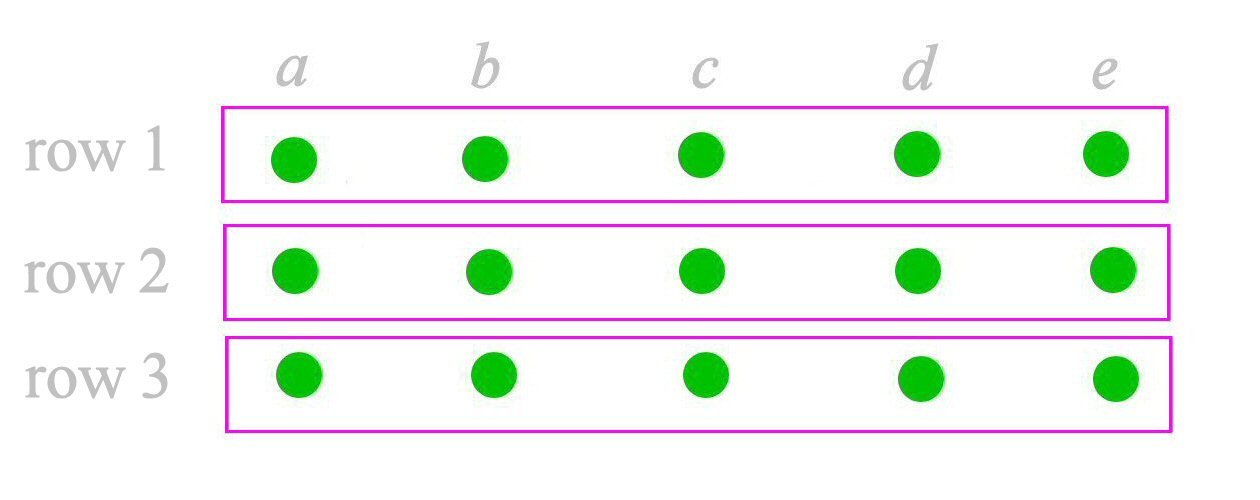
Suppose now we have three disjoint sets
{a1, b1, c1, d1, e1}
{a2, b2, c2, d2, e2}
{a3, b3, c3, d3, e3}
of 5 elements each. The total number of elements is 5 + 5 + 5 which is 3 × 5 (“three times five” or “three times of five”). Of course you know the value is 15, but I am here talking about the meaning of 3 × 5. The 5 appears 3 times in the addition. This is illustrated in the diagram below as 3 rows of 5 dots each.
Note however, that putting them as rows could be a cultural bias. Western languages are written horizontally from left to right. Arabic and Hebrew are written from right to left. The ancient Chinese wrote vertically, from the top down, and the columns proceed from right to left. So, if Georg Cantor was Chinese, teachers might be teaching pupils to add by columns instead!
Let us do some reorganisation. We take the set {a, b, c, d, e} and the set {1, 2, 3} and we form the Cartesian Product {a, b, c, d, e} × {1, 2, 3} of the sets, which, when we list down the elements, is
{(a,1), (b,1), (c,1), (d,1), (e,1),
(a,2), (b,2), (c,2), (d,2), (e,2),
(a,3), (b,3), (c,3), (d,3), (e,3)}
This is one set instead of 3 disjoint sets. But you can tell it has the same number of elements as the union of the three disjoint sets via an obvious bijection. For example (c,2) <---> c2.
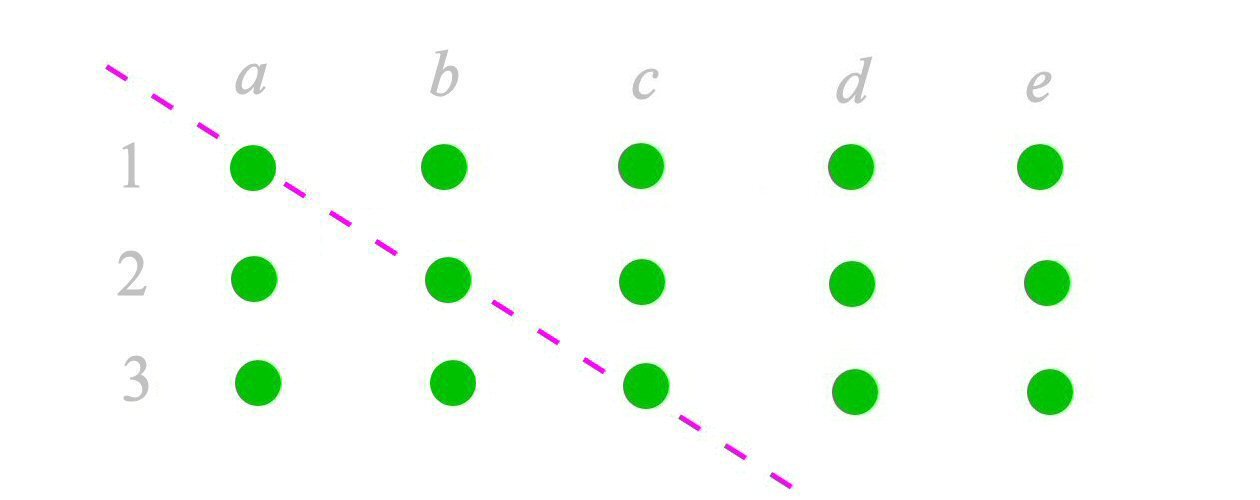
Next, let us do some reflection (no pun intended). Imagine there is a diagonal line running across from (a,1) to (c, 3) and we “reflect” the whole array in the diagonal line. This is what we get.

Rows become columns and columns become rows. I should have called it a matrix "transposition", but you know what I mean, right? Previously, we had 3 rows of 5 elements i.e. 3 × 5 = 5 + 5 + 5. Now we have 5 rows of 3 elements, or 5 × 3 = 3 + 3 + 3 + 3 + 3. If you look at the elements inside the Cartesian Product, we are just swapping the coordinates. There is a natural bijection (x, n) <---> (n, x). For example, (b, 3) in the former set now becomes (3, b). Because of this bijection, obviously the number of elements remains the same. In this sense, 3 × 5 = 5 × 3, and, of course both have the value of 15.
Tomorrow, I shall talk about what I feel regarding the controversy. Was the teacher being too strict in marking the pupil as wrong when she used 3 + 3 + 3 + 3 + 3 instead of the expected 5 + 5 + 5 to “solve” 3 × 5? Stay tuned.
