In Singapore the crucial Primary School Leaving Examination (PSLE) for primary 6 pupils is just around the corner. Parents, school teachers, private tutors are all anxious, perhaps even more so than the pupils themselves. It is widely-held view (whether or not this is true) that the results of this high-stakes examination would determine the secondary school the pupil goes to, and hence the ultimate fate of the his/her life. So this week is hot! Here is an interesting word problem at about the primary 5 level, but would still be enough of a challenge for the primary 6 pupils and their parents (and maybe their tutors).

This problem is quite tricky, which can cause someone to “lose his marbles”. Here is an attempted solution provided by a parent using some sort of “algebra”, but it is wrong. Can you identify the mistake or misconception?
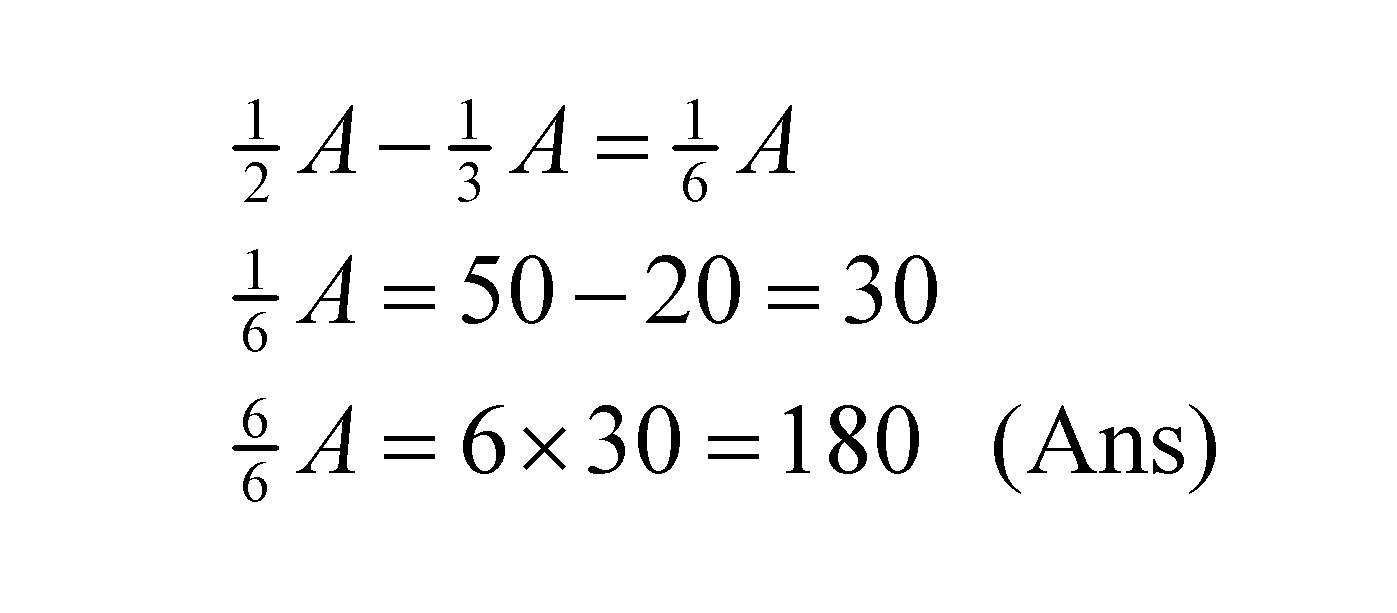
By the way, the use of algebra for solving this sort of word problems is optional in primary school. Many parents and tutors resort to using algebra to teach their pupils, because at primary 5 and 6, the problems tend to be so hard that drawing bar models is difficult or time-consuming. As the Chinese saying goes, one should not try to cut one’s foot in order to fit the shoe (削足适履). So although bar models are very useful for visualising and conceptual learning, especially at primary 3 and primary 4, one should be flexible in ones methods of attacking mathematical problems.
Nevertheless, there is a flaw in the above “solution”. The issue is that when one gives some number of items to another person, the difference is double that of the number given. For example, let us say that you and I start off with having 10 sweets (candies) each. Then I give you 3 sweets. I now have 3 sweets less, and you have 3 sweets more. That means I now have 7 but you have 13. The difference is 6, which is double the number of sweets transferred (3). So if Andy loses ½ A and Ben gains ½ A, the difference between the "before" situation and the "after" situation is double that, which is A! So the above working should be modified to 2/6 A = 30, which leads to the correct answer of 90.
I present below my own method of solution to this challenging problem, without using bar-diagram models and without using letter symbolic algebra.
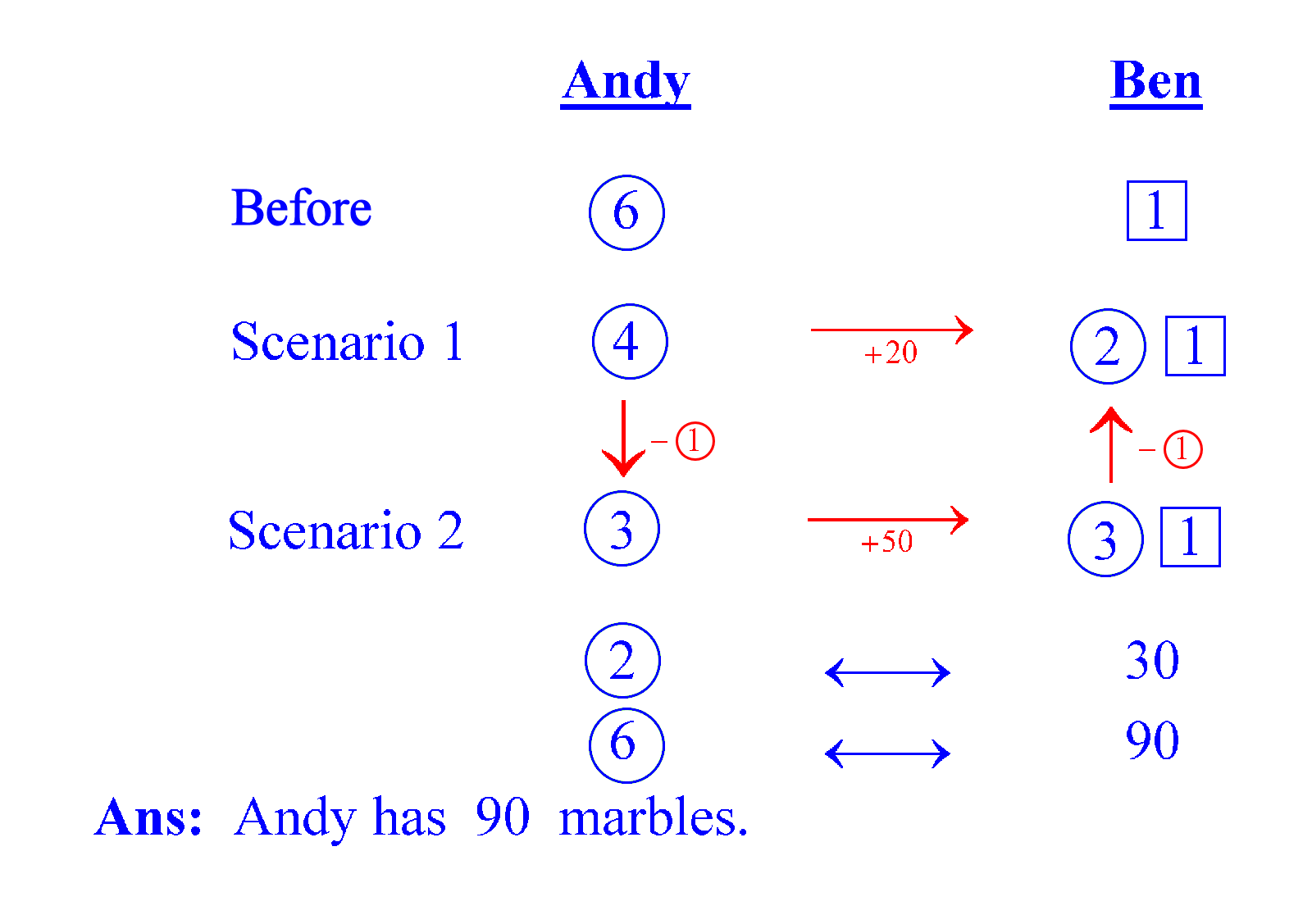
Let Andy’s intial holdings be 6 circled units for convenience (as it can be divisible by 2 and 3). Let Ben’s initial number of marbles be 1 unit (enveloped by a square), but this portion remains constant throughout. If Alan transfers 1/3 of his marbles to Ben, Alan has 4 circled units remaining and Ben gets 2 circled units. If Alan transfers 1/2 of his marbles, then each has 3 circled units. By comparing, we see that we need to drop 2 circled units to get from 50 to 20, so 2 circled units must be the same as 30. [ In other words, the difference between what Andy donated in the two scenarios is 1 circled unit, so the difference between Andy and Ben is 2 circled units. ] That means 6 such units is 90. Solved!
I envelop the different ratio units with different shapes e.g. circles, squares and triangles. I call them Distinguished Ratio Units (DRU), because the ratio units involved in this sort of word problems are often different and can be easily confused with one another and with absolute numbers. So, for example, a “squared” 3 units would be different from a “circled” 3 units which has a different meaning from the plain number 3. Some tutors and teachers in Singapore use “u” for “units” and “p” for “parts” to distinguish different sizes of ratio units, even though the words “parts” and “units” are synonymous in this context. This has become an evolved practice in Singapore, and can be said to be part of the “math sub-culture” in some learning places in Singapore.
In conclusion: Mathematics is not about following a fixed set of procedures. Bar diagrams are not the only or the best way to solve Singapore maths problems. There are many ways to skin a cat. But all roads lead to Rome!
