Take a look at the diagram below. You are given a circle of centre O and diameters AC and BD intersecting perpendicularly. You are given that the slanted chord CD is 8 cm long. Find the area of the circle (rounded to the nearest cm²).
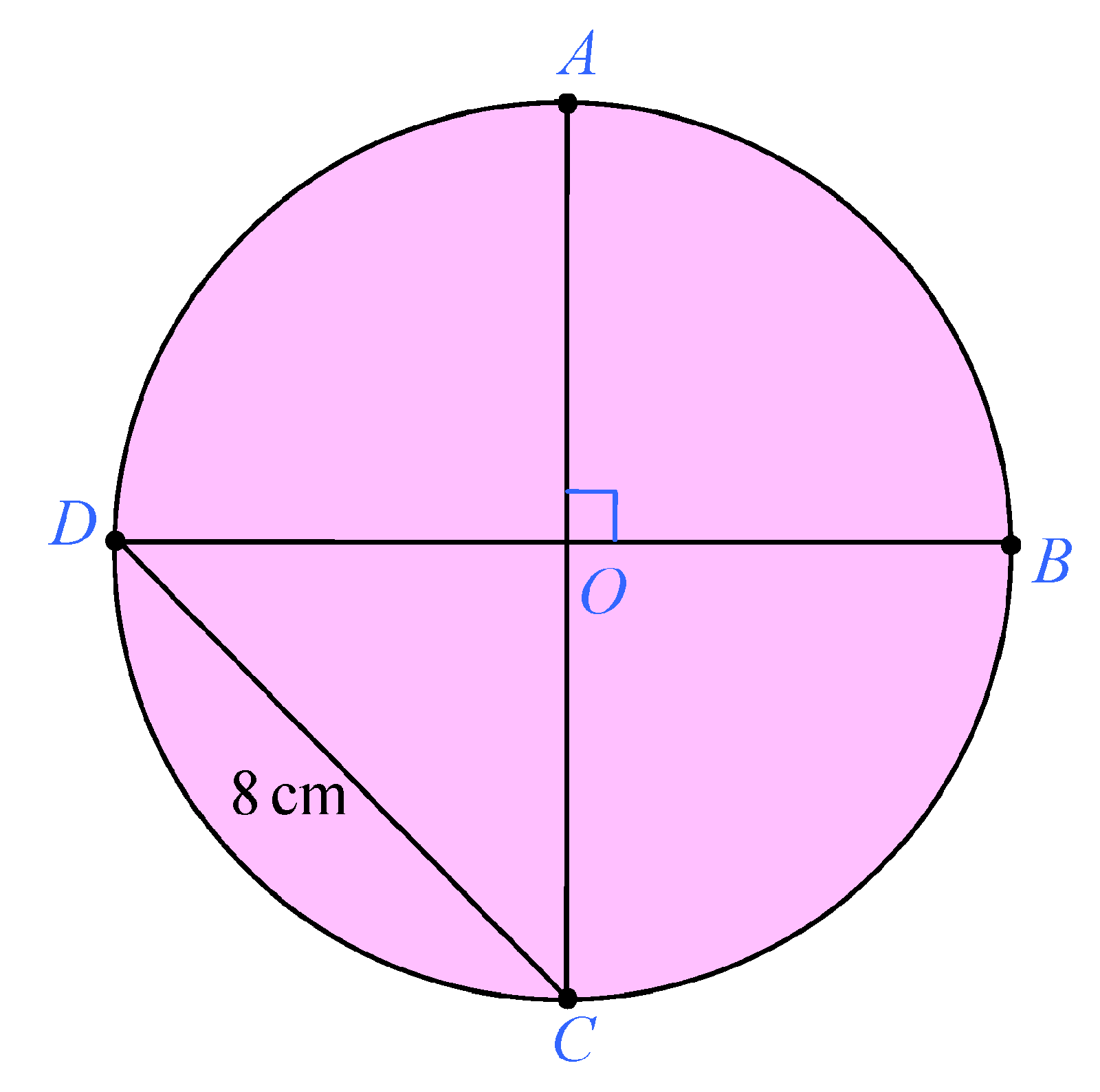
Well, area of a circle equals ... but what is the radius r? CD is 8 cm but it is not the radius. We are not given the radius. How to get the radius???
This problem is so hard! It must be “Singapore Math”! Yes, it is of Primary 6 level in Singapore schools. In Singapore, we just call it “maths”. And our maths is not always dealing with bar-model diagrams, although we seem to be famous for that.
Any ideas? Well ... er ... this has some right-angle ... so ... erm ... something like Pythagoras’ Theorem?
Sorry to burst your bubble, but in primary school, pupils have not learned Pythagoras’ Theorem. So try to do this without Pythagoras’ Theorem. Primary school maths is like fighting with bare hands. No advanced weapons. And that is why this is really challenging.
Think, think, think ...
OK, back to the idea about the r squared. If we can figure out r squared, we just need to multiply by . So maybe we can form a square using DO and OC. Draw lines parallel to DO and OC and let them meet at E. We have a square DOCE. Now if we can figure out r squared, which is the area of this square ...
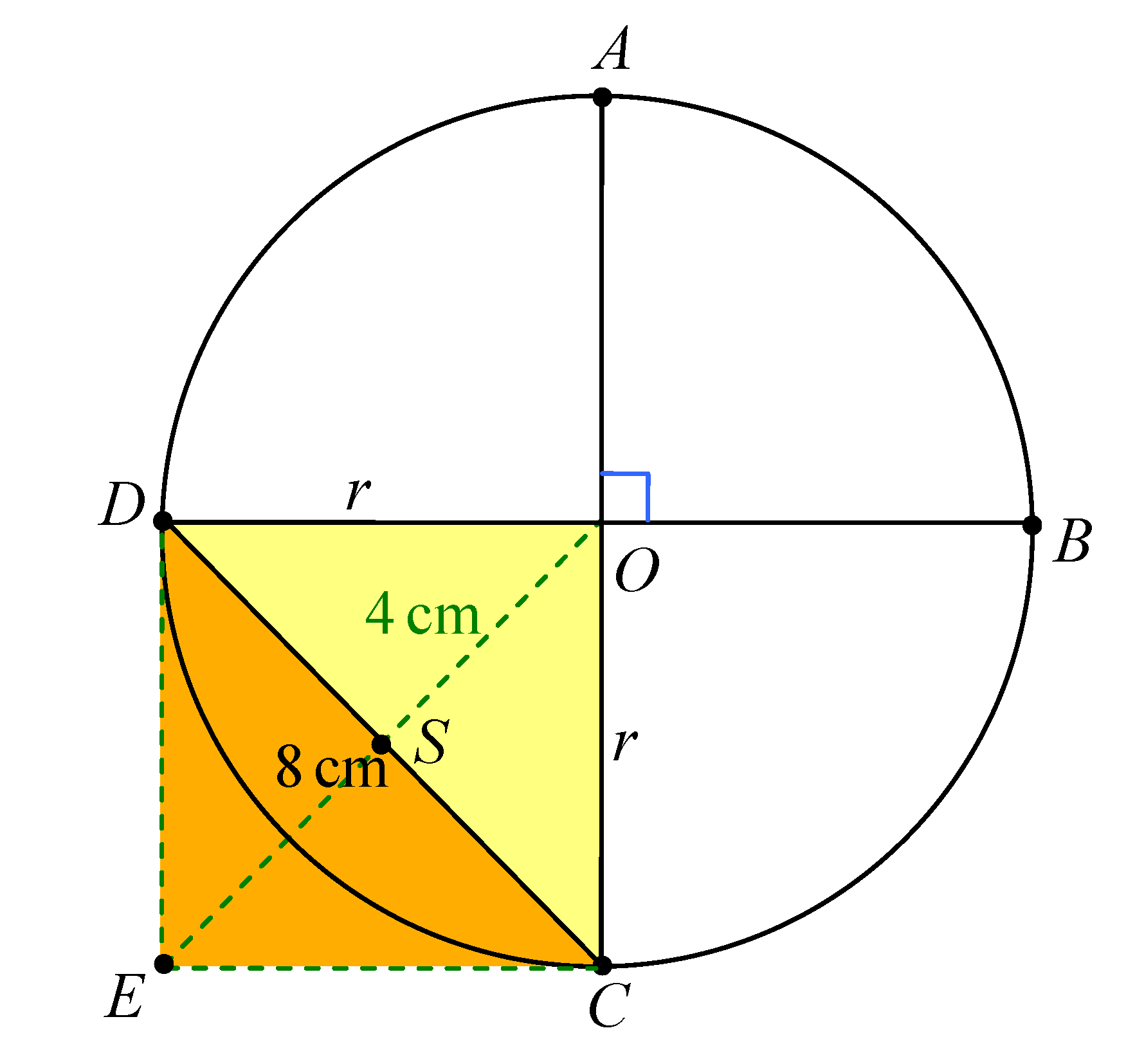
If we let OE intersect with DC, we get a point S which is the centre of the square DOCE. Notice that the diagonal OE is also 8 cm long. So SO is half of that, or 4cm. The area of triangle DOC is ½ × base DC × height SO =
½ × 8 × 4 = 16 cm². So the area of the square DOCE is double of that i.e. 32 cm². Mulitply this by pi = 3.1416, we get the area of the circle as 100.531 cm² = 100 cm² (rounded to the nearest cm²).
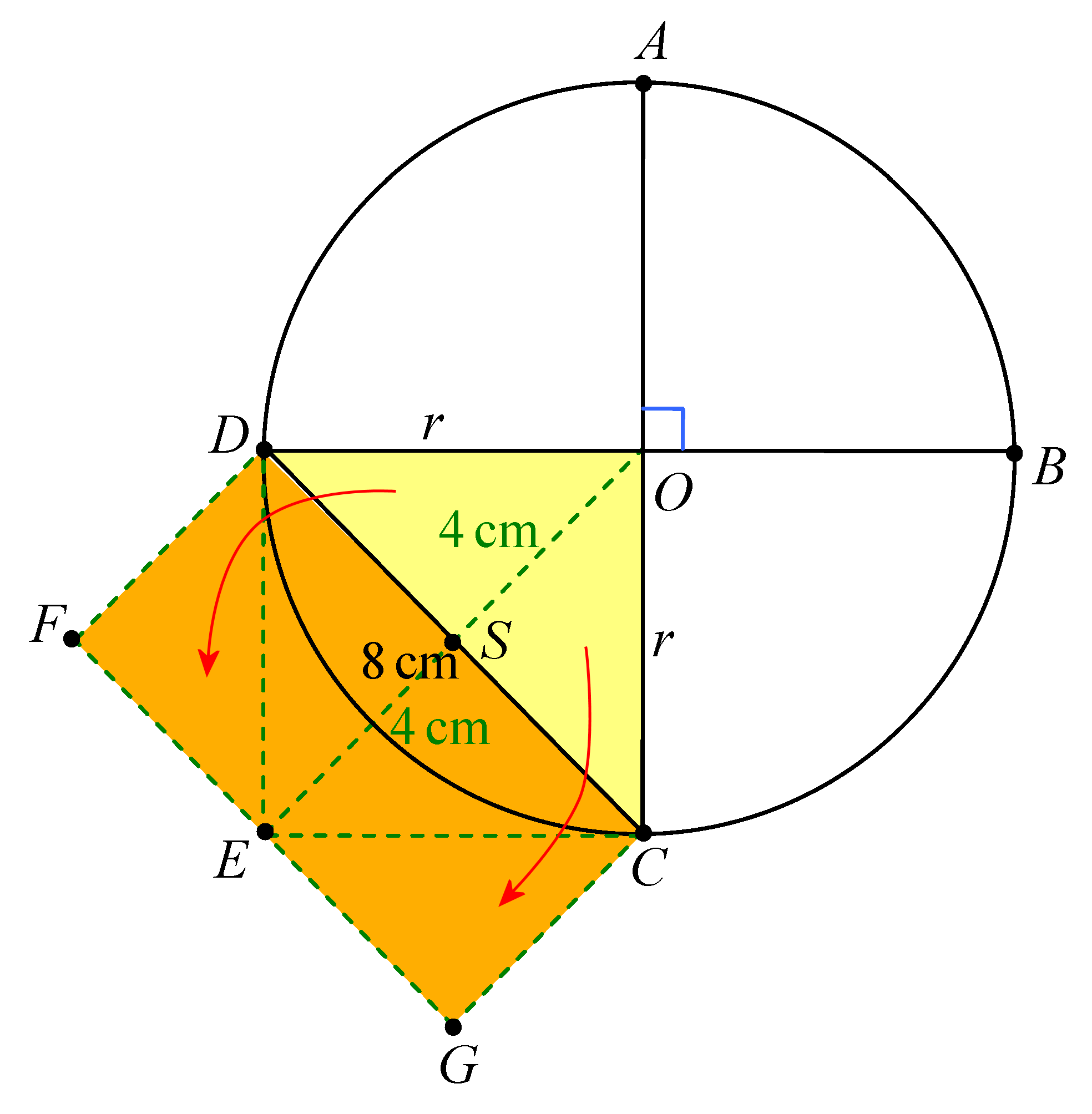
Incidentally, you may also get the area of the square DOCE by shifting the triangular pieces DSO and CSO around (shown in yellow above) to form a rectangle FGCD (shown in orange above). The height ES is 4 cm and multiplying with CD = 8 cm also gives us 32 cm².
So what have we learned here?
Sometimes we do not need very advanced mathematics to tackle a hard problem. We might break down the problem into a simpler problem (this is one of the problem-solving heuristics). There may be more than one way to solve problems. And using creativity, we may get a new slant (no pun intended) on the problem.
