This is a seemingly mind-boggling primary school mathematics problem from Singapore, for primary 4, or even primary 3. This is like our version of grade 4 elementary school, but on steroids. You may want to call it “Singapore math”, but in Singapore, we just call it “maths”. Some of us pronounce it, improperly, as “macks”.
ABCD is a square of side 10 cm and PQR is a right-angled triangle. The corner P of triangle PQR is placed at the centre of square ABCD. BX = 3 cm. Find the area of the quadrilateral PXCY.
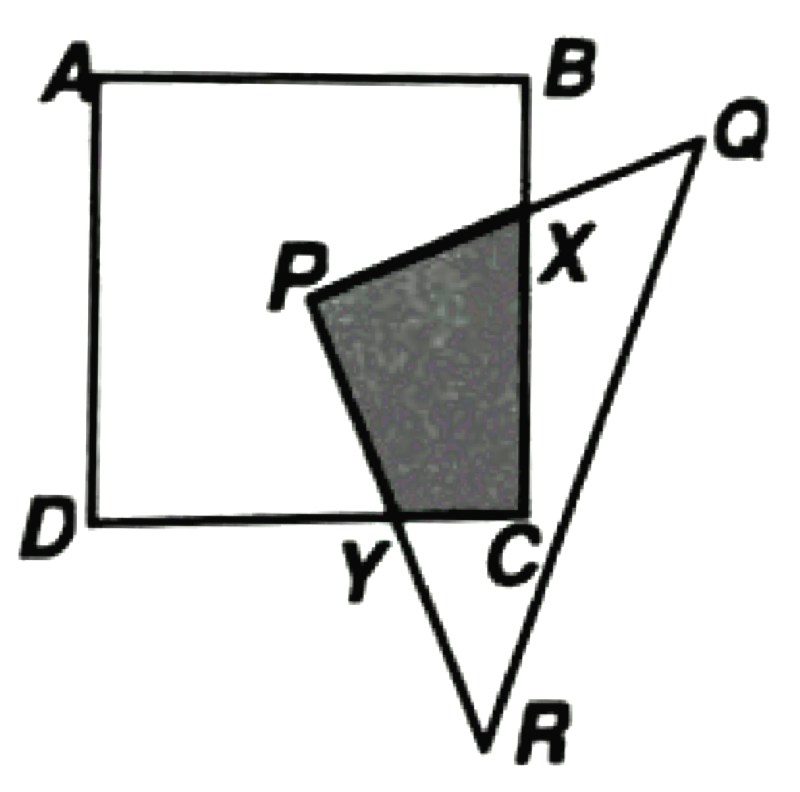
Challenging, eh?
How would you tackle this?
How do you begin?
Pause here.
Do not peep below.
Think about it.
Hint 1: Think of an equivalent problem (this is a heuristic).
Hint 2: Can you do things to the shape that does not change the area?
What we can do is to make an imaginary cut from P horizontally to the right, perpendicularly to BC. We get a piece in the shape of a right-angled triangle. We can take this right-angled triangle and move it down to re-join the shaded area at the lower side DC. (see diagram below). This looks like a rotation about P. We are just shifting the piece around, which does not change the area. But now the problem becomes really easy. It is just a quarter (or a fourth) of the big square ABCD! So it is ¼ × 10 × 10 or 25 cm².
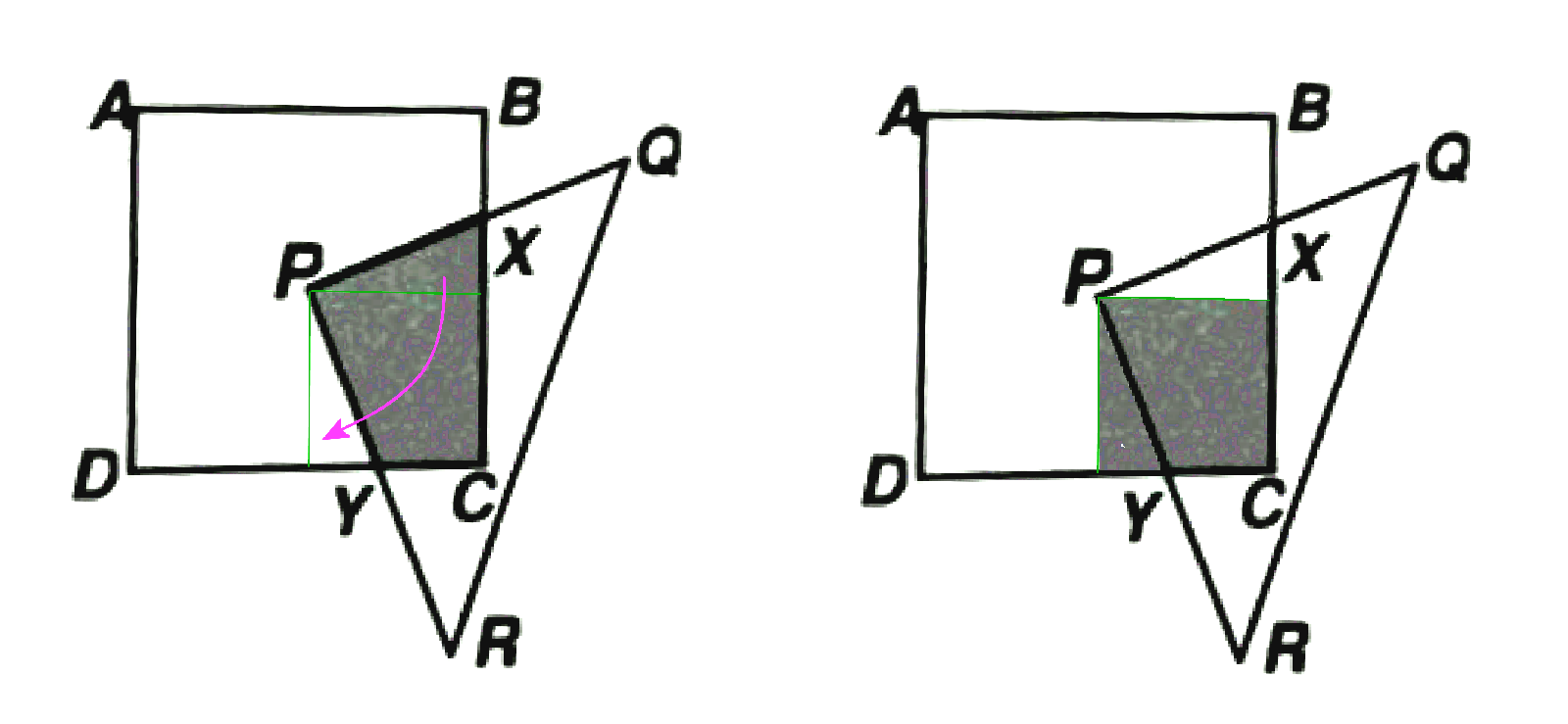
Notice that the fact that BX = 3 cm is irrelevant. If BX was 2.9 cm, or 3.01 cm, or any reasonable length for that matter, we could still have used the same “trick” and gotten the same result. So this is a distractor. The teacher who set this question was sneaky, eh? Is it fair? Well, mathematics is not just about arithmetic and calculation. It is also about great ideas like “areas are the same after shifting around (translations and rotations)”. Being able to judge the relevancy of a piece of information is also critical in school, as well as in life in general. This is an example of mathematics in the Singapore curriculum that really makes pupils (and even adult parents and tutors helping them) think! Thinking of a related problem is a powerful heuristic. Sometimes, problems can be solved by thinking of it in another way. With some creativity, you can make the cut! (no pun intended)
