Today I discuss the use of various heuristics to solve a Singapore primary mathematics problem, at about our primary 5 (grade 5) level. Take a look at the word problem given below.

The original wording was “earned” instead of “collected”, but maybe the teacher who set this question forgot that what you collect is not necessarily what is earned, because of the cost of the rice and operating costs.
The structure of this sort of problem is that of a system of simultaneous linear equations in two unknowns. So this is quite challenging. To rub salt to the wound, primary school pupils in Singapore are taught only rudimentary algebra in grade 5 or 6. In primary (elementary) school, pupils are like fighting with bare hands instead of using weapons. That is one of the reasons why Singapore mathematics is so challenging. Singapore’s curriculum planners at our Ministry of Education do not necessarily require pupils to use advanced mathematics. They want pupils to be good problem solvers, using one or more recommended heuristics from the official list of 11. Actually there are many more problem-solving heuristics, as outlined in my blog post elsewere. I shall illustrate 5 methods of solution using various (versions of) heuristics. Note that drawing bar-diagram models, for which “Singapore math” is famous, is just one of the ways to draw diagrams, which is just one of the 11 recommended heuristics for primary school. It is said that “there are many ways to skin the cat”. Here I shall skin the cat in 5 ways. Don't worry: cats have 9 lives. So in the end, the cat still has 4 lives remaining :-) .
Method 1: (not-so-systematic) Guess-and-Check
Our first method uses the “guess-and-check” heuristic. We randomly try some combination of 5.8-kg packets and 4.2-kg packets. If it is correct, we are done. If not, try other different combinations of 5.8-kg packets and 4.2-kg packets until we get the correct combination.
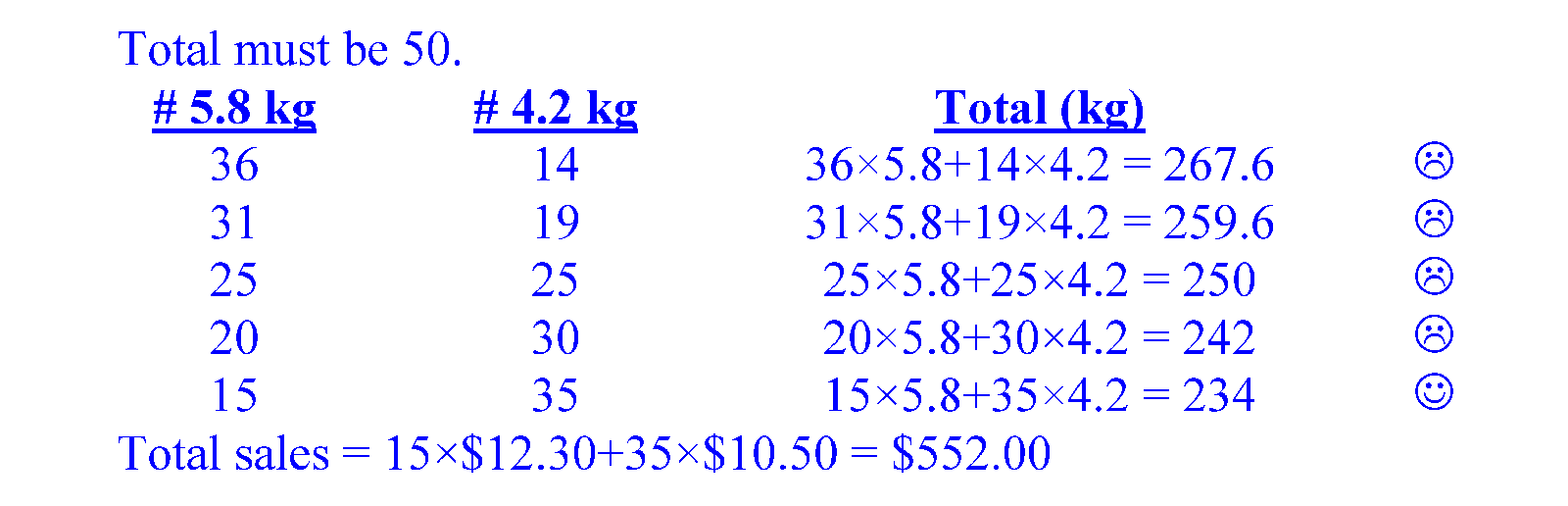
If we had 36 5.8-kg packets and 14 4.2-kg packets, we would have 290 kg. Wrong.
If we had 31 5.8-kg packets and 19 4.2-kg packets, we would have 259.6 kg. Naaaaah! Try again!
We get the general idea that we need to reduce the number of 5.8 kg packets. After three more attempts we get the correct combination of 15 5.8-kg packets and 35 4.2-kg packets. From here, we can work out the total revenue. This method of guess-and-check (a.k.a. trial-and-error) works, but it is tedious. Can we do it a bit more systematically?
Method 2: (Systematic) Guess-and-Check
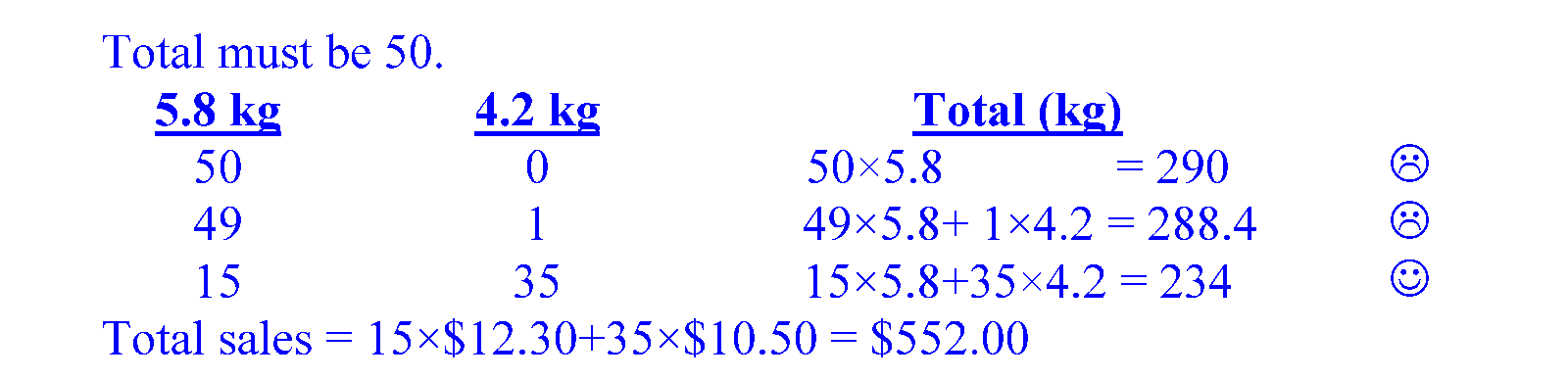
Hypothetically assume all the 50 packets of rice are 5.8 kg packets. The total mass would be 290 kg. Let us replace one 5.8 packet with a 4.2 kg packet. We get a total mass of 288.4 kg. We notice that when we change one 5.8 kg packet with a 4.2 kg packet, the total mass drops by 290 kg – 288.4 kg = 1.6 kg. The gap between 290 and 234 is 56. To achieve that required amount of reduction, we would need 56 ÷ 1.6 = 35 such swaps. So we try 15 5.8 kg packets and 35 4.2 kg packets and it works. We can work out the total revenue as usual.
For the Systematic Guess-and-Check method, we assume all the packets of rice are of one type, we replace one kg of one type by the other type to see its effect, we work out the change in the total mass (290 kg – 288.4 kg = 1.6 kg), we also work out the gap between the first trial and what needs to be achieved (290 – 234 = 56). By division, we can work out how many units need to be swapped (56 ÷ 1.6 = 35) and that leads to our answer. Hey! Do you notice something? Could we have predicted the difference of 1.6 kg without going through the hard calculation? Yes! Just take 5.8 kg – 4.2 kg = 1.6 kg. That saves some work! Notice also that we could have assumed that all the packets of rice were 4.8 kg packets and worked our way up. This leads to our third method.
Method 3: Making an Assumption + Logical Reasoning

The “Difference between packets” is 1.6 kg means that every 4.2 kg packet swapped with a 5.8 kg packet would increase the total mass by 1.6 kg. This solution is perhaps the most succinct, with no visual representation. It requires a lot of experience and understanding on the part of the student. For people who have never seen this sort of problem, very few would think of solving it this way. This method is not recommended for novices.
Method 4: Bar Diagrams
I illustrate my bar diagram below. The use of bar models can sometimes be quite challenging, like in this case, because you do not know how many bars to draw. And the number of bars required is in fact the main problem to be solved.
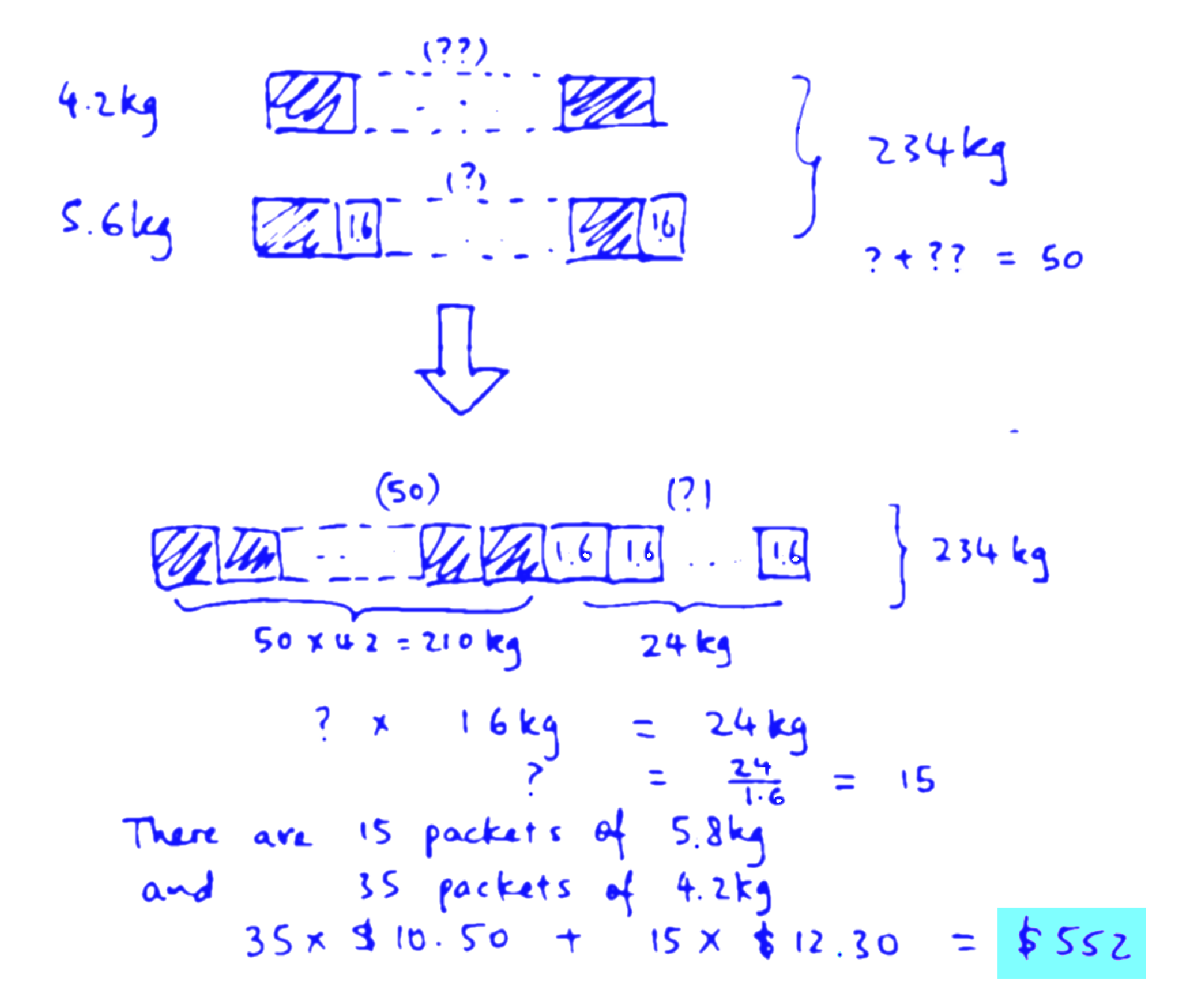
In the upper half (above the big arrow), I was just trying to make sense of the question. Understanding the problem is the important first step in the problem solving process. There is some unknown number (??) of 4.2 kg packets (each of which is represented as a shaded block). There is some other unknown number (?) of 5.8 kg packets, which are each treated as a shaded block (4.2 kg) plus 1.6 kg. Their total weight (or more correctly, mass) is 234 kg. The two unknown numbers ? and ?? total 50. I take all the 50 shaded blocks (representing 4.2 kg each) and line them up and put the 1.6 kg blocks together. I know that the 50 shaded blocks are worth 210 kg by calculation. The shortfall of 24 kg (234 kg – 210 kg) is made up of the 1.6 kg blocks which number the same as the 5.8 kg blocks (because that is where those extra 1.6 kg blocks came from). So how many of such blocks are there? Take 2.4 divide by 1.6 and that gives the answer 15. The rest of the problem unravels quite easily, as explained in the other methods above.
Method 5: Diagramming via Distinguished Ratio Units
This is my own style of solving the word problem without the (formal) use of algebra. I let 1 “square” unit represent the unknown number of 4.2 kg packets, and I let 1 “triangle” unit represent the unknown number of 5.8 kg packets. This is called Distinguished Ratio Units as I use different shapes to envelop the different units, because these units represent most likely different quantities. I want them to be seen as different types of things, so as not to get muddled up.
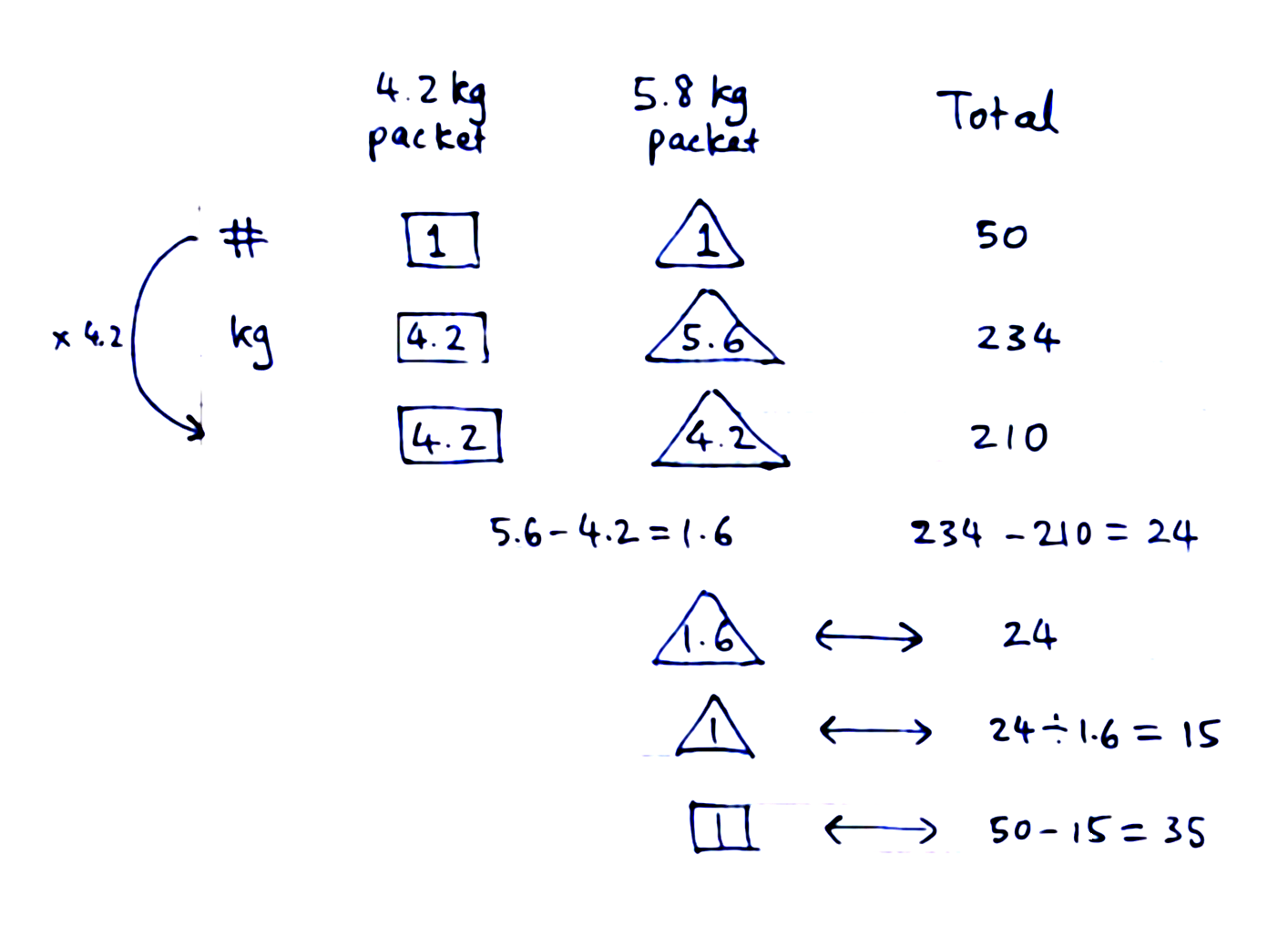
Total sales = 15×$12.30 + 35×$10.50 = $552
In terms of number, one “square” unit and one “triangle” unit total up to 50.
In terms of mass (in kg), one “square” unit times 4.2 and one “triangle” unit times 5.6 total up to 234.
I multiply everything in the first row by 4.2 to get the third row. Comparing the second row and the third row, the 4.2 “triangle” units are equalised, so the difference of 1.6 triangle units accounts exactly for the difference of 24 (kg). Again we divide 24 by 1.6 to get 15 for 1 “triangle” unit. 1 “square” unit can be easily seen to be 35. From here, we can work out the total sales in dollars.
Whew! Congratulations if you have read all the way till the end here.
I have demonstrated five different non-algebraic methods for solving a challenging word problem from “Singapore Math” (in Singapore, we just call it “maths”). I hope you examine each of them. Tell me which one you like best.
