I hereby introduce a new way of looking at the Chain Rule for differentiation, which I called the “Onion Method for differentiation”. It will be apparent why it is so called. Let us consider the following example, done by the old-fashioned Chain Rule.
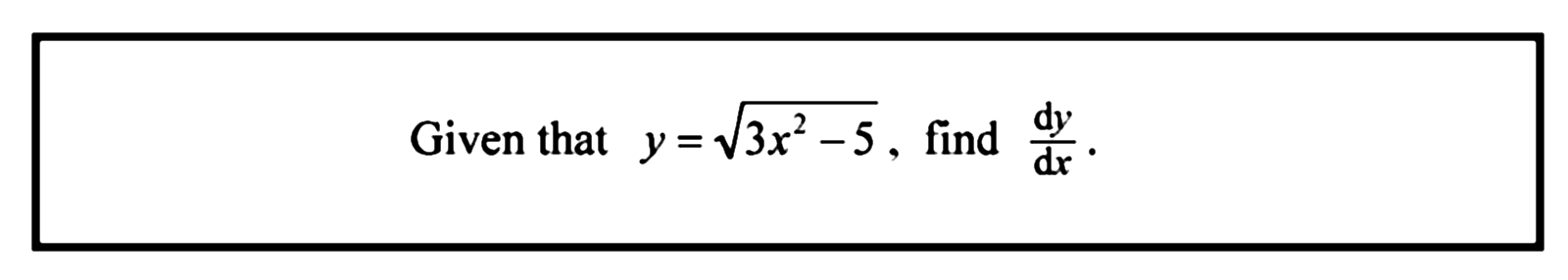
First, we write the square root as a power of half. Seeing that 3x² - 5 is wrapped inside a pair of brackets (or parentheses), we substitute u for that expression. According to the chain rule, we do dy/du and multiply that by du/dx. dy/du is done using the power rule, where the ½ is carried down, and then index ½ is reduced by 1 to negative half. To do du/dx, the 2 is brought down from 3x² to multiply with the 3 to give 6, and the index 2 is reduced by 1. Actually, x¹ = x and we do not usually write the 1 index. 5 becomes 0 when differentiated.
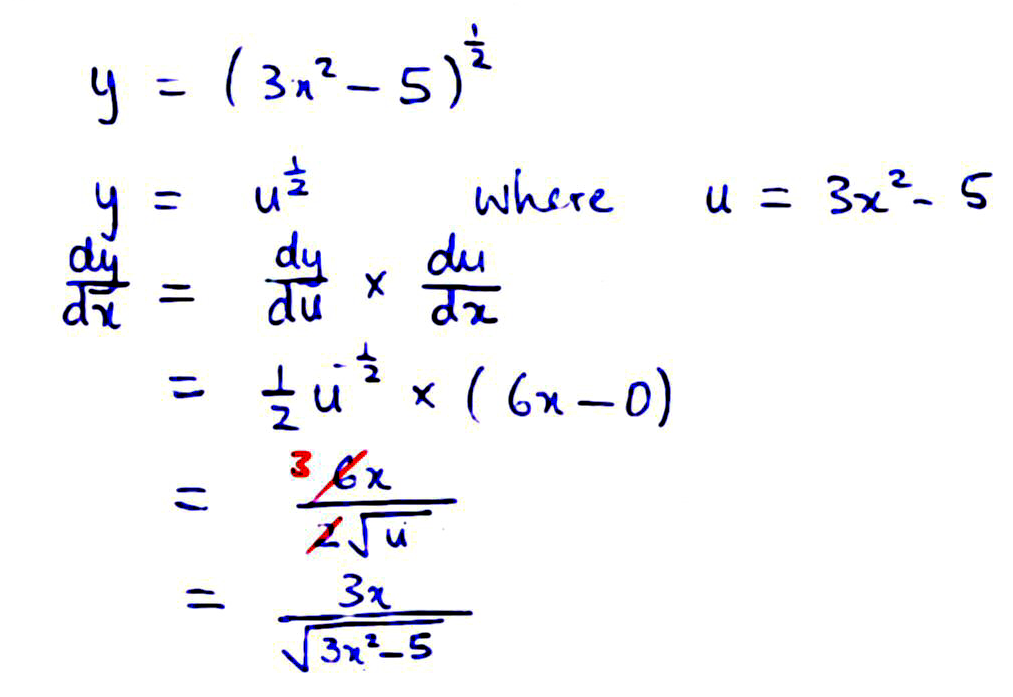
Let us tidy up. The ‘2’ from the big ½ goes downstairs. The little ½ index means “square root”, and negative means “divide” or “go down as the denominator”. So we write square root of u below the fraction bar. 6x goes on top. The number 6 cancels with 2, to get 3. And so we get the simplified answer.
Once you understand the above principle, you can do it faster. Draw rings around the expression, which is a function within a function. This looks like an onion with an outer layer and an inner layer. [ Alternatively, you can think of Matryoshka dolls from Russia, where upon taking out a doll, you find a smaller doll inside it. ]
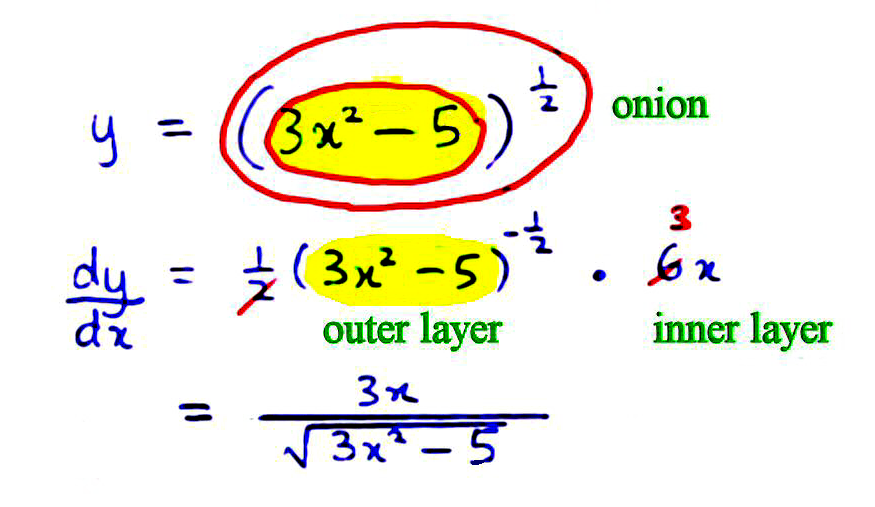
When you peel onions, you peel the outer later and then inner layer(s). Likewise, we differentiate the outer layer first, and work our way in. For the outer layer, copy down the ½ and reduce the index ½ by 1 to get -½ . Copy and paste the whole inner core (shown in yellow) verbatim. Put a dot for multiplication. Now we differentiate the inner layer, which yields 6x. Then we cancel and simplify.
If you compare the two presentations, you will find that they are the same, except that the Onion Method does not use an explicit ‘u’ substitution. The ‘u’ is actually the whole yellow patch, and we copy and paste the whole thing. We get the same result, but faster. I hope you find this useful.
