In an earlier article I described the power of Euler’s formula and the idea of rotation. Much of it is theory. But how do you know what happens when the rubber hits the road? The following problem I concocted will illustrate the power of Euler’s formula. Read the following question and try to solve it.
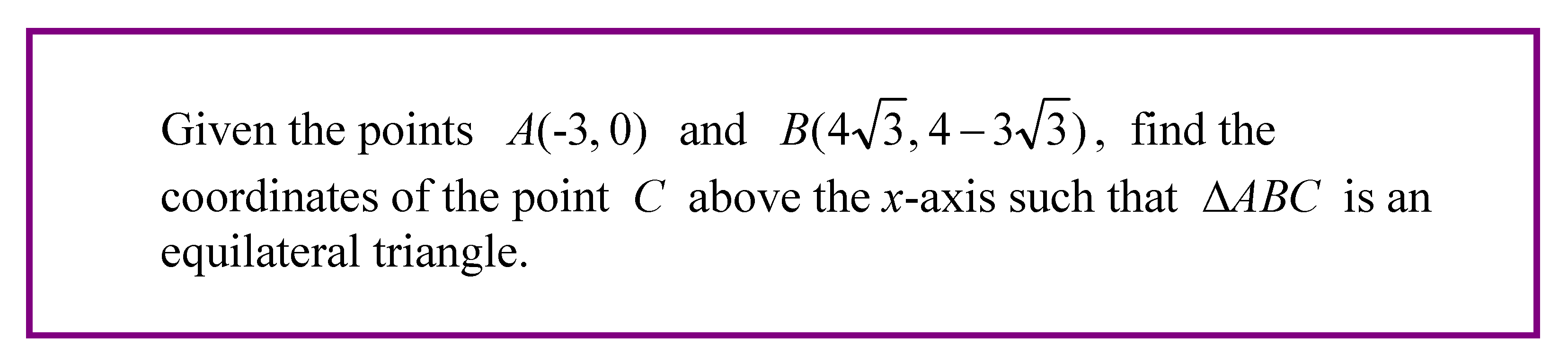
Attempt 1
OK, let us try to use a coordinate geometry method that mimics a ruler-and-compasses construction. So using r = AB as radius, we construct two circles with that radius with centre at A and another one of the same radius centred at B. The two circles will intersect at two possible points. We reject the point that is below the x-axis. The working may look something like this:-

Even if you do not hang yourself, you are likely going to get a hangover trying this. How about trying another tactic?
Attempt 2
We may use the fact that the trigonometric tangent of the angle that a line makes with the x-axis is exactly the same as the lines gradient (slope). We calculate the slope of AB and that gives the tangent of its angle with the x-axis. Add 60° anticlockwise (or counterclockwise). We may use the trigonometric compound angle tangent formula to get the gradient of AC. From here, maybe try to intersect with BC ... no ... that would be another tedious calculation ... or maybe trying to find the point along AC that is the same distance as AB ... sounds workable ... OK, let’s try it!

This is soooooooo stressful! Why do I suddenly have a craving for a lollipop?
Attempt 3 : Euler to the rescue!
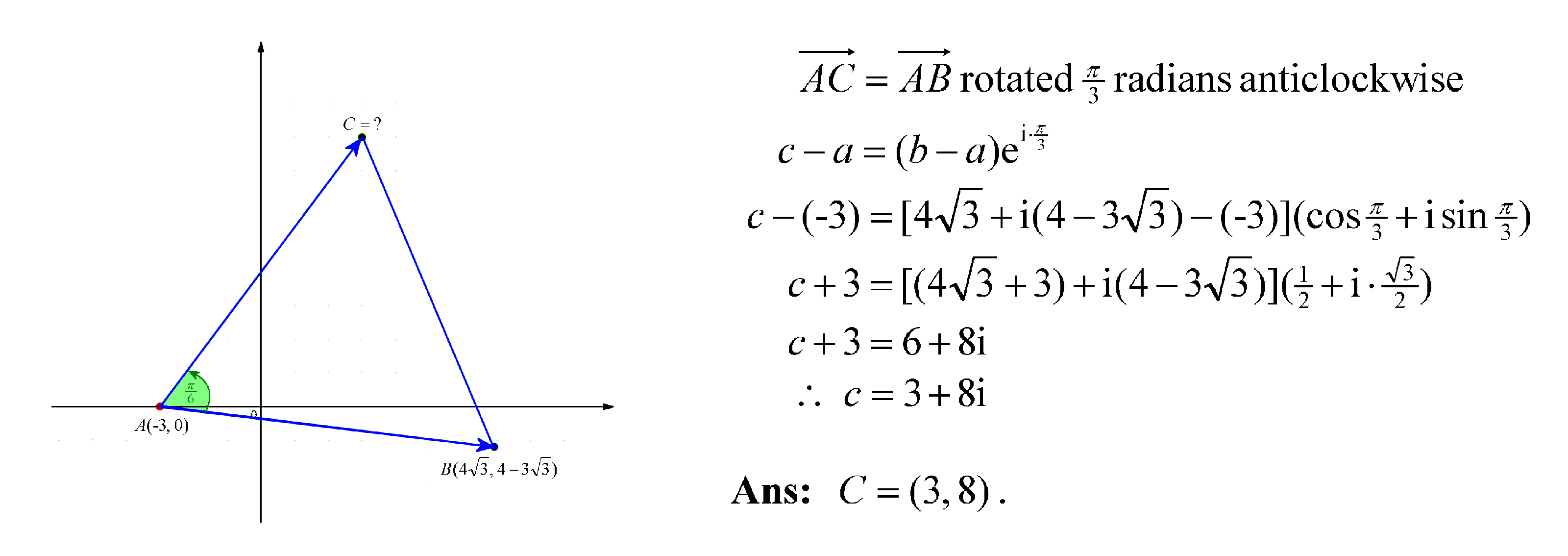
In the equilateral triangle, all sides are equal and all the angles are 60 degrees. So vector AC is just vector AB rotated by 60 degrees anticlockwise. In perfect analogy with vector arithmetic, the vector AC corresponds to the complex number c – a and the vector AB corresponds to the complex number b – a . As explained in my earlier article, using complex numbers, rotation by anticlockwise angle is achieved by multiplication with
. In this case,
, so we multiply by
. Substitute in the numbers. After about 3 lines of working, the answer comes out easily.
With Euler’s help, we do not need to hang ourselves, get a hang over or eat lollipops, damaging our health in the process. Life becomes a breeze! Kewl, eh?
Cheers!
Do you think you really understood the foregoing technique? If so, you may want to try this problem from the 1994 American Invitational Mathematics Examination Question number 8.

If you are game for a challenge, try this one from Sixth Term Examination Paper (STEP) Mathematics Exam 1987 Paper 2 Question 4. STEP is the very tough examination used as entrance examination for reading mathematics at the University of Cambridge and other universities.

