Let’s see how many of you can do this ...
Are you ready?
Here goes ...

Think!
Don’t peep!
Think some more!
Come on! You can do it!
Got it?
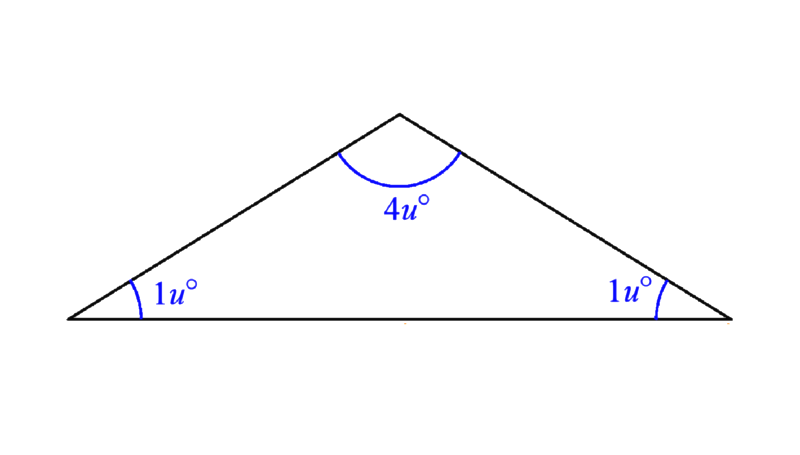
What is your answer? If you think the anwer is 2 : 3, then you are wrong! Gotcha!
You may have thought: there are 6 ratio parts which total 180°. So 1 part is 180° ÷ 6 = 30°, and 4 parts is 30° × 4 = 120°. Considering the sides opposite their respective angles, we have the ratio 120° : 180° or just 4 : 6 = 2 : 3 and that is the answer.
What is wrong with that? Well, the ratio of the angles is not the same as the ratio of their opposite sides.
Tricky, eh? So how to do this correctly?
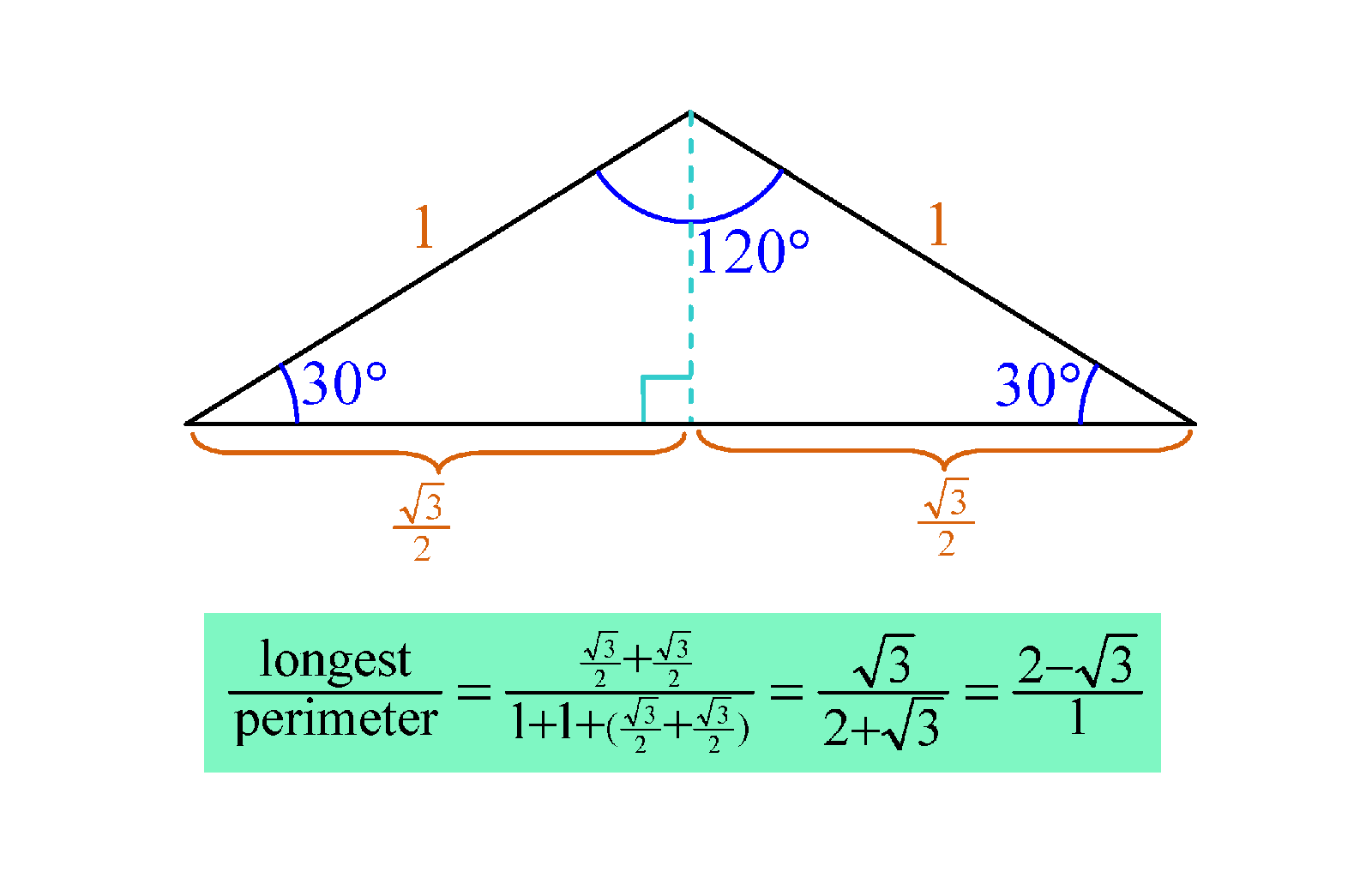
Draw a 120°-30°-30° triangle and let the sides opposite the 30° be 1 unit (for convenience). If you drop a perpendicular from the 120° vertex to its opposite side, you cut the triangle into two congruent halves, each of which is a right-angled triangle. Using basic trigonometry for right-angled triangles (a.k.a. “toa cah soh” or something like that), we can figure out each half of the longest side as being . Remember that cosine = adjacent ÷ hippopotamus ... i mean ... er ... hypotenuse, and cos 30° =
. So the ratio of the longest side to the perimeter works out to be
:
, or equivalently,
: 1, which happens to be also the same as 1 :
. Decimally, it works out to be 1 : 2.15 or thereabouts.
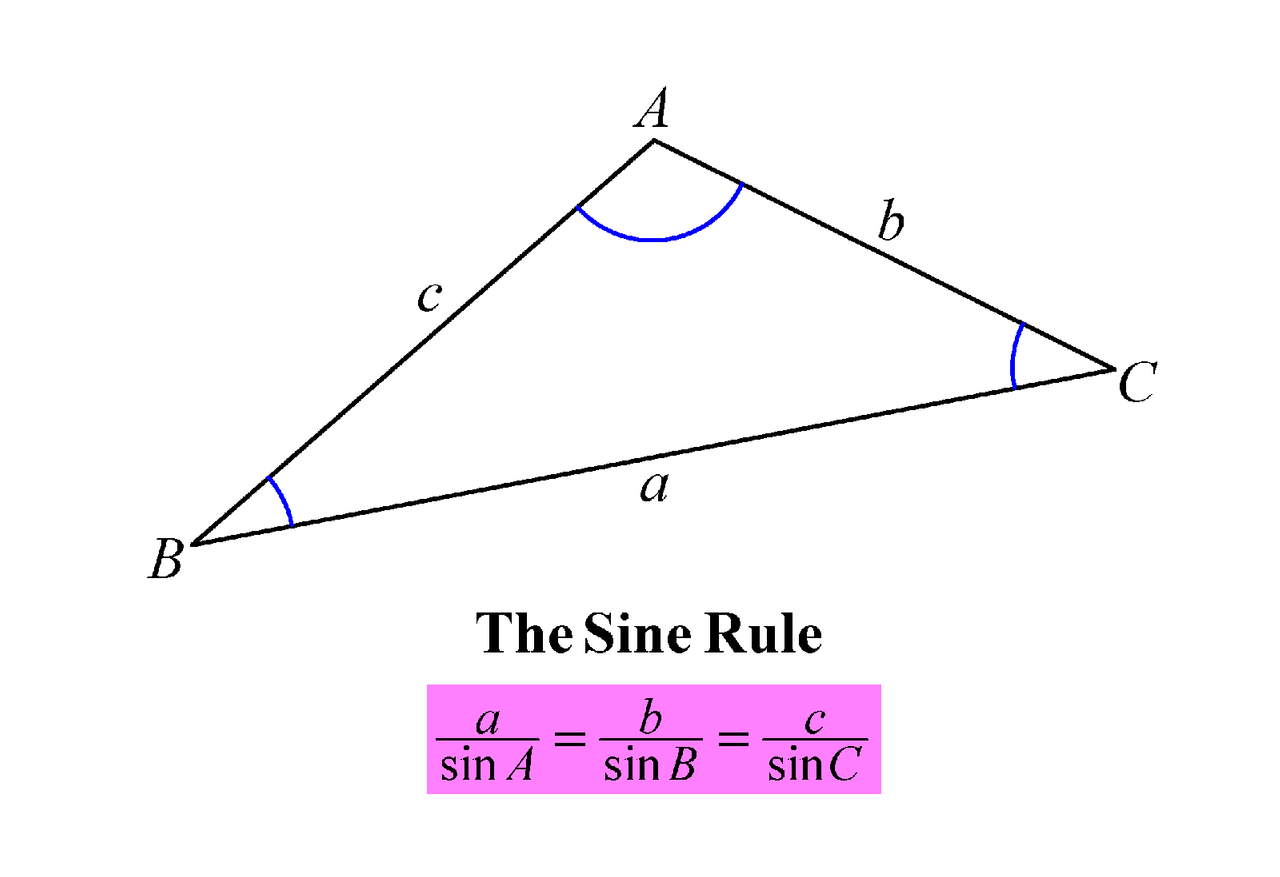
OK, suppose now we are not given 4 : 1 : 1 as the ratio of angles. What happens in the general case? Well, in the general case, we would need to appeal to the Sine Rule or the Law of Sines.
The Sine Rule basically says that the ratio of the sides is proportional not to their respective opposite angles, but to the sines of those angles. Thus, for the general case, the answer would be sin A : sin A + sin B + sin C, if A is the largest angle.
I hope you have learned something from this tricky problem. Don't feel bad if you have got it wrong. There is something new to learn every day.