Here is the third episode of my particle physics crash course that will be given at CERN, on February 9th, prior to the moment where 20 Steemians will enter the LHC to visit the CMS detector. With this series of posts, I intend to browse all the glory details underlying the world of the elementary particles.

After focusing on the structure of matter (here) and on the form of the interactions between the fundamental particles (there), it is now time to discuss what the two guys on the above picture have done to get the Nobel prize in 2013.
THE SUCCESS OF GAUGE SYMMETRIES
In the previous episode, I have described what gauge symmetries are and how the interactions between the fundamental particles are modeled as gauge boson exchanges. In the Standard Model, we have a bunch of these bosons, also known as force carriers mediating the fundamental forces of nature.
One or more than one of them is associated with each of the fundamental interactions. Those are the photon (related to electromagnetism), the W-boson and the Z-boson (related to the weak interaction) and the gluons (related to the strong interaction). I recall that gravity is ignored.
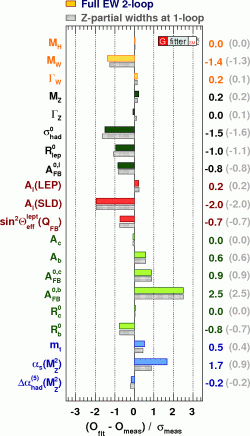
[image credits: the GFitter collaboration]
But why are those gauge symmetries important? Well, because the underlying predictions have been tested in several thousands of different measurements during more than 50 years.
There is up to now (almost) not a single sign of any deviation! This is the reason why the Standard Model is accepted so far as the model describing the world of the fundamental particles.
The level of agreement is illustrated on the picture on the left.
One can observe the differences, expressed in standard deviations, between theory and data for about 15 measurements. I recall that we need 3 sigmas for a hint for a new phenomenon, and 5 sigmas to claim for a discovery. Everything is thus fine.
We can thus explain most data with gauge symmetries. Almost. There is indeed a drawback. The gauge symmetries enforce all particles to be massless, which is not verified in nature. But on the other hand, it cannot be too wrong, as it works so well…
SUPERCONDUCTIVITY TO SAVE THE SHIP
In the 1960s, Philip Anderson, one of the world expert on superconductivity, realized an important point. He was studying superconductivity and observed that when a theory exhibits both some gauge symmetries and a spontaneous breaking of the gauge symmetry, the massless gauge bosons were actually getting massive.
The underlying mechanism is by no way different from the well known Brout-Englert-Higgs mechanism of particles physics, except for special relativity that is not necessary for superconductivity. Well-known? Well maybe not outside particle physics. But this does not matter for the rest of this post, where the important features will be sketched (tagging @sco here) :)
The relativistic example was provided 2 years later, in this publication written by François Englert and Robert Brout and this one by Peter Higgs, which is probably why Anderson is less known in the field.
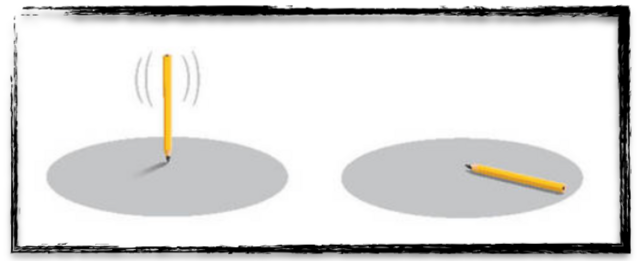
[image credits: a bit everywhere online]
But what is spontaneous symmetry breaking?
It can be explained with a pencil, as shown on the figure on the right.
On the left panel of the figure, the pencil holds vertically, assuming that it is somehow held. As soon as one lets it go, it goes and falls (the right panel).
But in which direction can it fall? Any is the answer. The pencil can fall anywhere in the gray circle.
This means that the ensemble of all solutions has a revolution symmetry around the pencil axis (the pencil axis on the left panel of course). However, as soon as the pencil falls, the symmetry is lost. One says that it is spontaneously broken. It is exactly the same thing for the case of gauge symmetries.
THE RISE OF THE HIGGS BOSON
In the Standard Model, one only needs one ingredient to implement the spontaneous breaking of the electroweak gauge symmetry: a scalar field (i.e. the Higgs field). The self-interactions of this scalar field are known as the scalar potential. And as for any potential, it has to be minimized to understand how nature works.
There is an infinity of solutions minimizing the potential an the ensemble of solutions possesses a symmetry (like our pencil before falling). Nature picks one (our pencil falls), and the symmetry is broken.
As a consequence, the W and Z bosons get massive, but there is a remnant of the symmetry breaking mechanism, an extra particle called the Higgs boson. On top of that, the Higgs field can also be used to make all fermions massive! This is a kind of 2 for 1 sale, as we all know that matter is massive!
Why is this working? Why is this the mechanism chosen in nature? Well, again, data tells us.
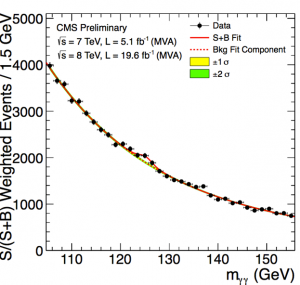
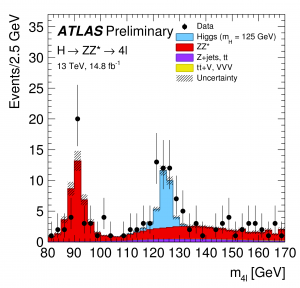
[image credits: the CMS and ATLAS collaborations]
The figure on the left is one of the CMS results that have led to the discovery of the Higgs boson. CMS investigated LHC collisions in which two photons are produced. The dashed line is the no-Higgs prediction, whilst the red line (the fit of the data points) consists in what is observed. There is a little bump in there, compatible with a Higgs boson.
The error bars are so small that there is less than one chance on almost 2 millions that this is not a signal.
On the right figure, it is a more recent figure, from ATLAS, where physicists have scrutinized a four-lepton final state. The Higgs boson is predicted to contribute via a decay into intermediate Z bosons). The red is here the background, and the blue the Higgs signal. Data is clear enough, once again :)
Today, the situation is even better: the properties of the Higgs boson are fully compatible with the expectation of the Standard Model, as shown by CMS and ATLAS.
There is however one caveat. the LHC is not the right machine to precisely measure the form of the Higgs potential… It can barely constrain it, and a future machine is thus necessary for getting the final words of this story.
SUMMARY
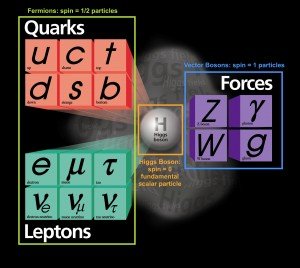
[image credits: Fermilab]
In this post, I finalized my introduction to the Standard Model of particle physics.
All the particles shown on the left have been introduced. The matter component (left part) was detailed here, the interactions were discussed there and in this present post, I discussed the Higgs boson.
In my future posts, I will detail how we managed to discover the Higgs. This requires two ingredients: theory and data. I will thus describe how to make predictions out of the Standard Model, and how to observe a Higgs signal in CMS (as this is the detector we will visit during the meetup).
The associated slides are available at the same address as before. More information can also be found in particular in this textbook (which I would use for introducing particle physics to bachelor students). This is also a great blog article on the Higgs mechanism.
SteemSTEM
SteemSTEM is a community-driven project that now runs on Steemit for more than a year. We seek to build a community of science lovers on Steemit and to promote well written/informative Science Technology Engineering and Mathematics (STEM) postings in order to make Steemit a place for fascinating STEM content.
More information can be found on the @steemstem blog and on the Steemit chat and in our last project report.
