You might have heard about the P vs NP problem, but what is the L vs. P problem?
Introduction
P and NP are famous complexity classes that measure the amount of time necessary for a Turing machine to decide a language.
Less famous are the complexity classes that measure the amount of space that a Turing machine uses. These are classes like PSPACE (polynomial space), NPSPACE (nondeterministic polynomial space) and EXPSPACE (exponential space). Just like time complexity has a hierarchy theorem, the Space Hierarchy Theorem demonstrates that every asymptotic separation between (computable) functions products a separation between space complexity classes. That means that there are problems which require O(n^2) space, problems which require O(n^3) space, problems which require O(n^3.1415) space, and problems which require O(2(2n)) space.
LSPACE
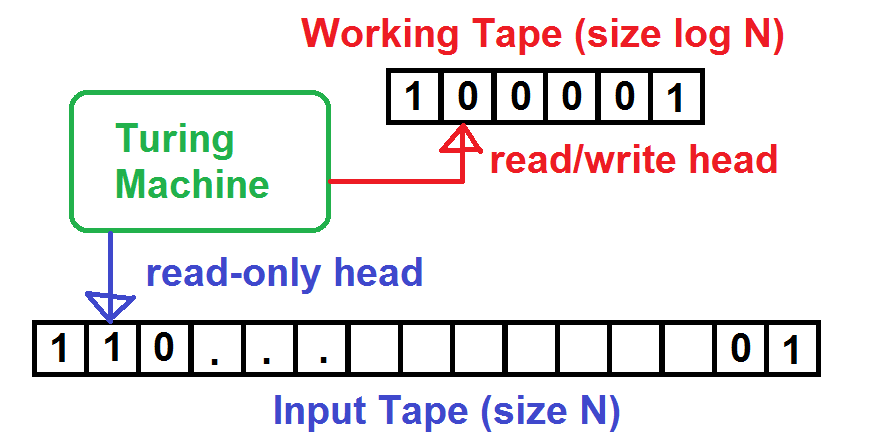
The class L, or LSPACE, contains all decision problems that a deterministic Turing machine can solve using only a logarithmic amount of writable space, relative to its input size. It can also be written as DSPACE( log n ).
Obviously a Turing machine needs to read its input which is already of size n. We can work around this by giving the Turing machine two tapes: one read-only for the input, and one read-write for its working space. The Turing machine can use the working space to store a constant number of "pointers" into the input, or a logarithmic number of constant-sized working areas.
In 2004, Omer Reingold showed that the decision problem USTCON is in L. USTCON is a decision problem on an undirected graph; it simply asks whether there is a path between two given nodes "s" and "t"; hence "Undirected s-t CONnectivity." This was an important advance that put a lot of problems previously known to be reducible to USTCON into L as well, including:
- Do two undirected graphs have the same number of connected components?
- Is there a cycle in a graph, that contains a given edge?
- Is an input graph bipartite?
Some of these are quite tricky to solve using only logarithmic space; conventional graph algorithms often use steps which are O(n) space in the worst case, such as depth-first search. A 2008 version of Reingold's paper can be read here: https://omereingold.files.wordpress.com/2014/10/sl.pdf
L vs P
Despite this relatively recent advance, there is a larger open question: is L, the class of decision problems requiring logarithmic space, distinct from P, the class of decision problems requiring polynomial time?
One direction is easy; we can see that every problem in L must be in P. If a Turing machine uses O(log n) space on a binary tape, then the tape can only be in 2^O(log n) = n^O(1) different states. (The Turing machine itself contributes only a constant number of extra states.) So, if a Turing machine in L halts, it must halt in a polynomial amount of time. So L ⊆ P.
But, the reverse direction is unknown. We don't have a way to show that every decision problem in P can be run in logarithmic space, which seems unlikely. But neither do we have any decision problem in P that we can conclusively demonstrate must take more than logarithmic space.
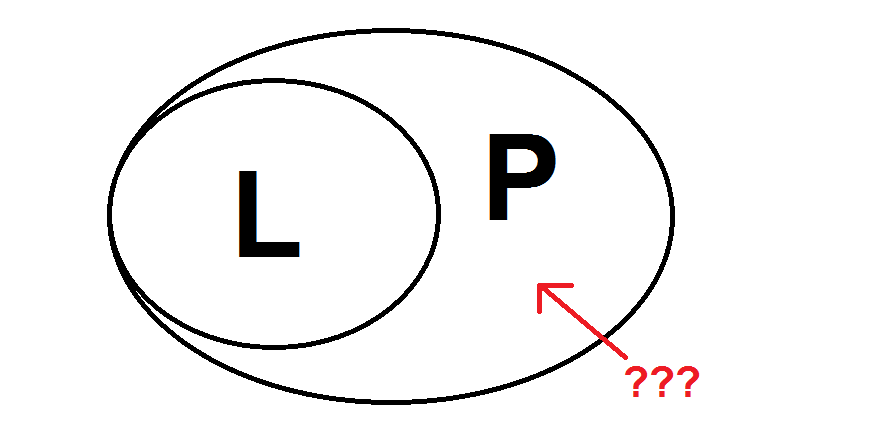
To me, that's more amazing than our current inability to resolve P vs. NP. We know that there must be problems that require O(n) space. But we can't prove any of them have a polynomial time bound. And we know that there are problems that require O(n^20) time. But we can't prove that any of them have a space bound that's greater than O(log n).
We also don't know, given logarithmic space usage, whether nondeterministic Turing machines can solve any decision problems that deterministic Turing machines can't; that is, if L = NL or L != NL.
Sources and Further Reading
L (complexity) at Wikipedia
Logarithmic Space at the Complexity Zoo and the now-equivalent SL
Taking Passes at NP Versus L a blog about a near-separation result
